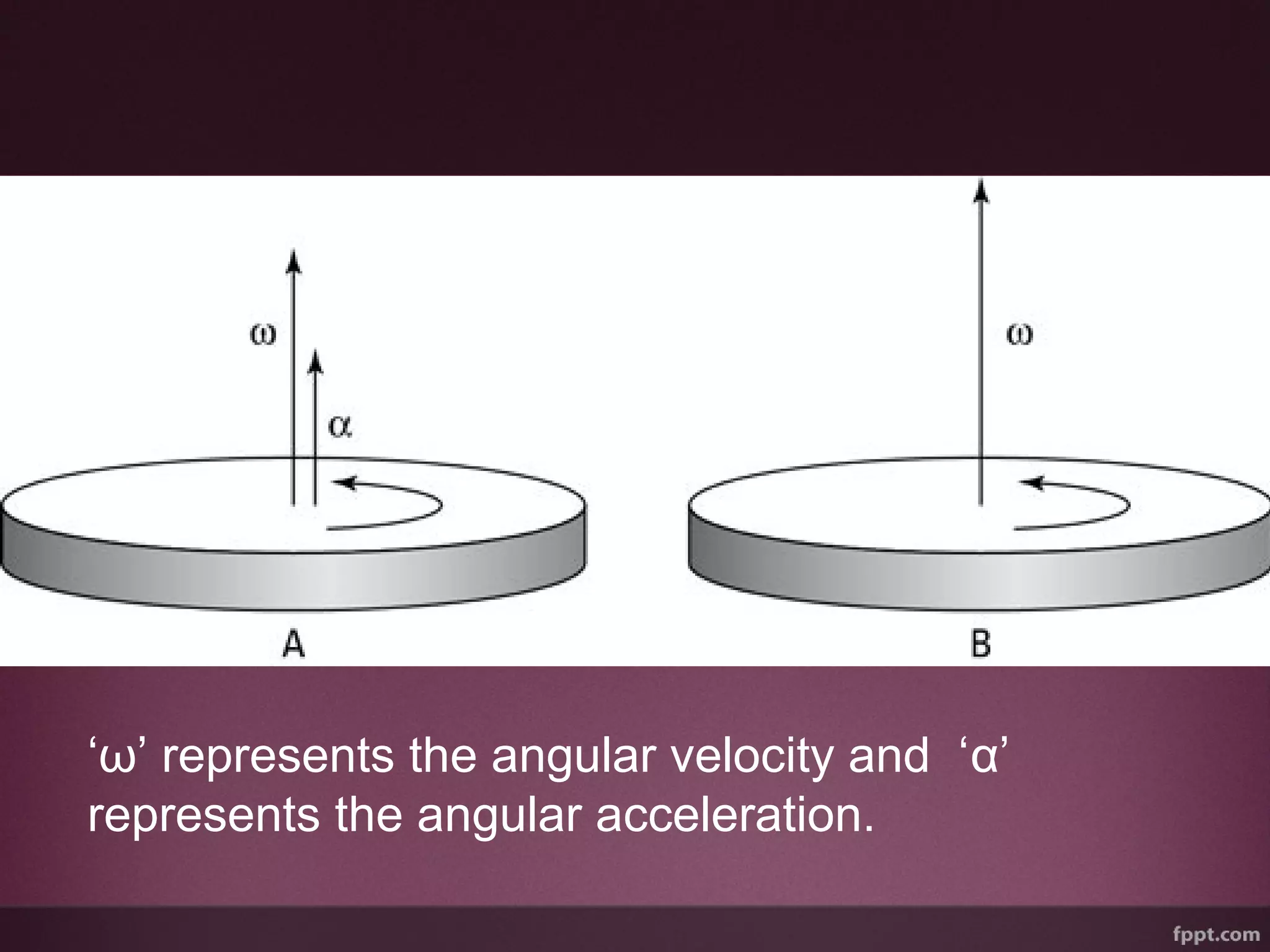
This document discusses circular motion and related concepts. It defines circular motion as motion along a circular path and uniform circular motion as motion with a constant speed. It describes angular displacement as the angle through which an object rotates and defines the SI unit as radians. Angular velocity and centripetal acceleration are introduced as concepts to describe rotation and the inward acceleration experienced by objects in circular motion. Centripetal force is defined as the inward force causing this centripetal acceleration according to Newton's second law of motion.

1. CIRCULAR MOTION

2. CONTENTS
• CIRCULAR MOTION
• ANGULAR DISPLACEMENT
• ANGULAR SPEED
• ANGULAR VELOCITY
• CENTRIPETAL FORCES &
ACCELERATION

3. CIRCULAR MOTION
• If an object/ body is moving along a
circular path it is said to be in circular
motion.
• Uniform circular motion : If the object
move with uniform speed along the
circular path, it is said to have uniform
circular motion.
• http://www.animations.physics.unsw.edu.a
u/mechanics/chapter3_circularmotion.html
#3.1

4. Angular displacement
• The angle through which the radius
vector representing the position of a
particle rotates is called angular
displacement
• The change in position of the particle in
a circular path with respect to its centre
is called angular displacement.
• The angular displacement of a body
with respect to a reference line is
denoted as θ.

5. Angular Displacement Units
• The angular displacement can be
measured in degree.
• But the S.I. Unit for angular displacement
is Radians.
• One radian is defined as the angle
subtended at the centre of a circle by
an arc which is equal to length of the
arc divided by the radius of the circle.

6. Conversion between degree
and radians
• When an object makes through a
complete circle,
• angular displacement in the entire circle
is 3600
= 2π radians
• 1 0
= 2π/ 180
• 1 radian = 180 / 2π degrees

7. Question to check how far you
understood
• By how many degrees does the angular
displacement of the hour hand of a clock
change each hour ?

8. Speed steady , but velocity ?
• An object moving in uniform circular motion is
moving in a circle with a uniform or constant
speed.
• Is it accelerating ?
• Yes, because, it is changing the velocity.
• Since velocity is a vector which has both
magnitude and direction, a change in either the
magnitude or the direction constitutes a change
in the velocity.

9. Angular velocity
• Angular velocity, also called rotational
velocity, is a quantitative expression of the
amount of rotation that a spinning object
undergoes per unit time.

10. Vector – angular velocity

11. Centripetal acceleration
• An object moving in a circle is
experiencing acceleration. Even if moving
around the perimeter of the circle with a
constant speed, there is still a change in
velocity and subsequently an acceleration.
This acceleration is directed TOWARDS
THE CENTER of the circle.

13. ‘ω’ represents the angular velocity and ‘α’
represents the angular acceleration.

14. Centripetal force
• According to Newton’s second
law of motion, every object which
has an acceleration will
experience a net force in the
direction of acceleration.

15. Centripetal force
http://w3.shorecrest.org/~Lisa_Peck/Physics/syllabus/mechanics/circularmotion/Images/
wi1.gif
So for an object moving in a circle, there
must be an inward force acting upon it
in order to cause its inward acceleration
which is called centripetal force.
The word "centripetal" means CENTER-
SEEKING. For objects moving in circular
motion, there is a net force acting
towards the center which causes the
object to seek the center.

16. Centripetal force
http://www.regentsprep.org/regents/physics/phys06/bcentrif/default.htm
http://phet.colorado.edu/en/simulation/legacy/gravity-and-orbits

17. Questions.
End of the chapter questions.