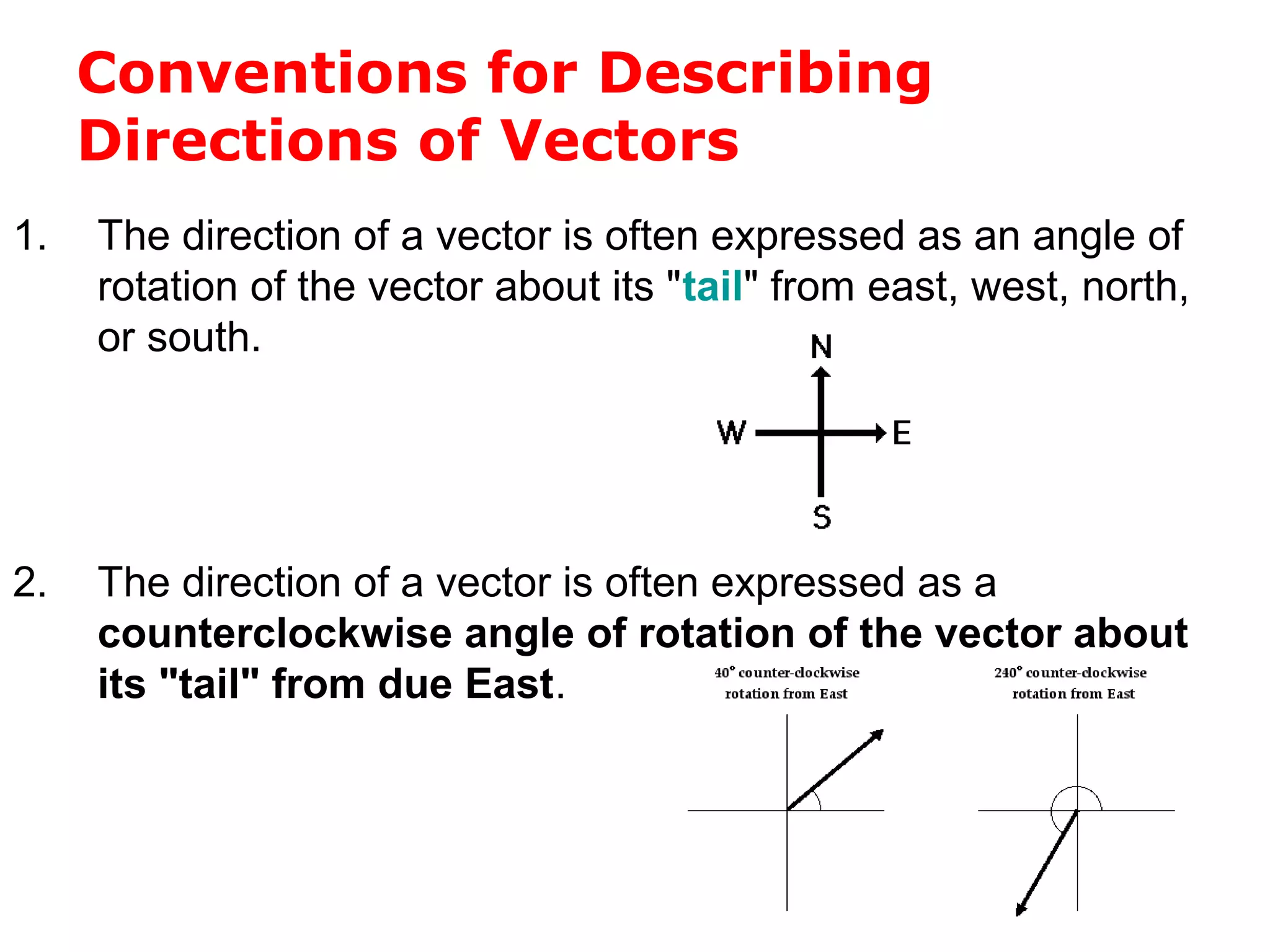
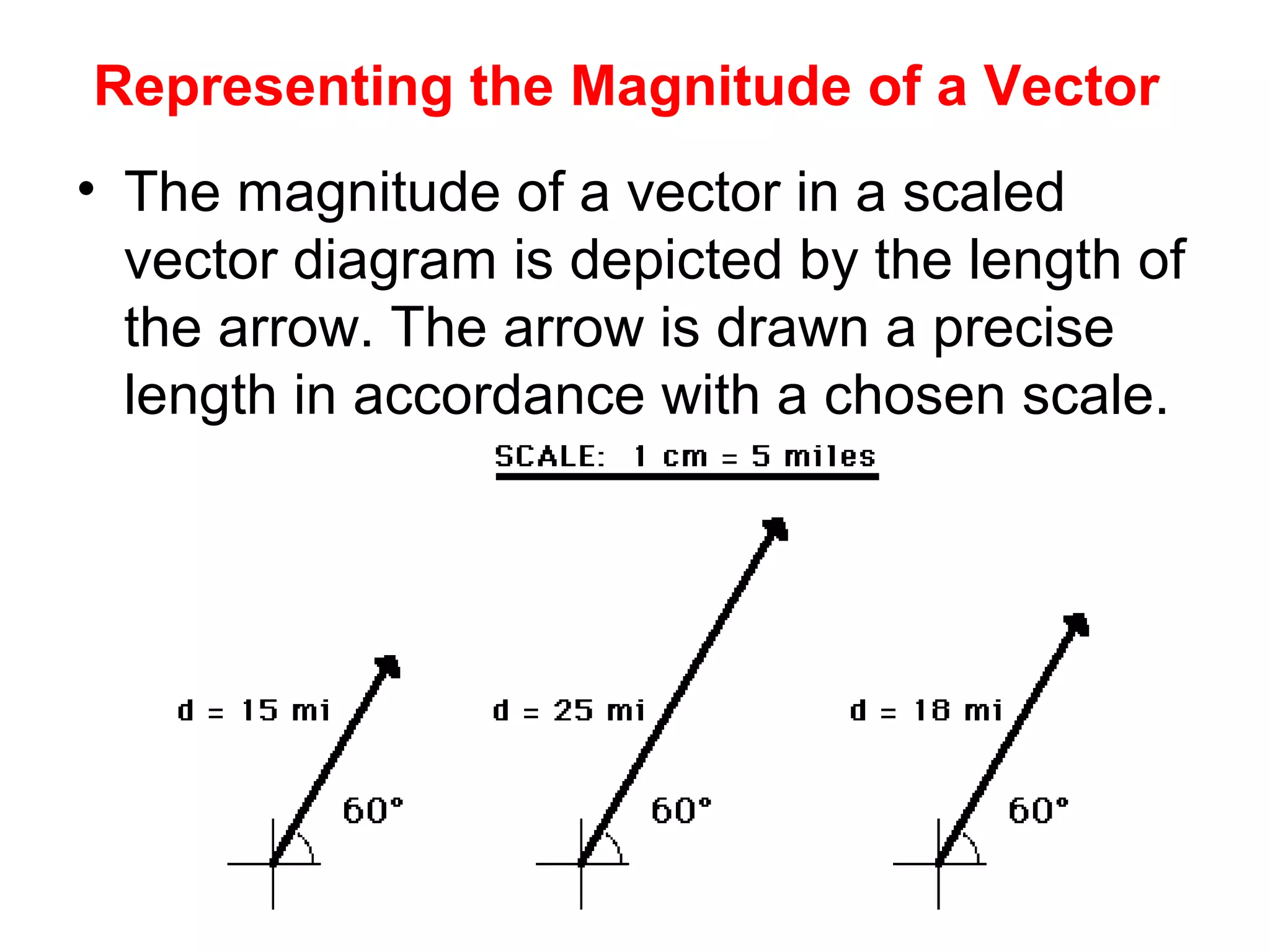
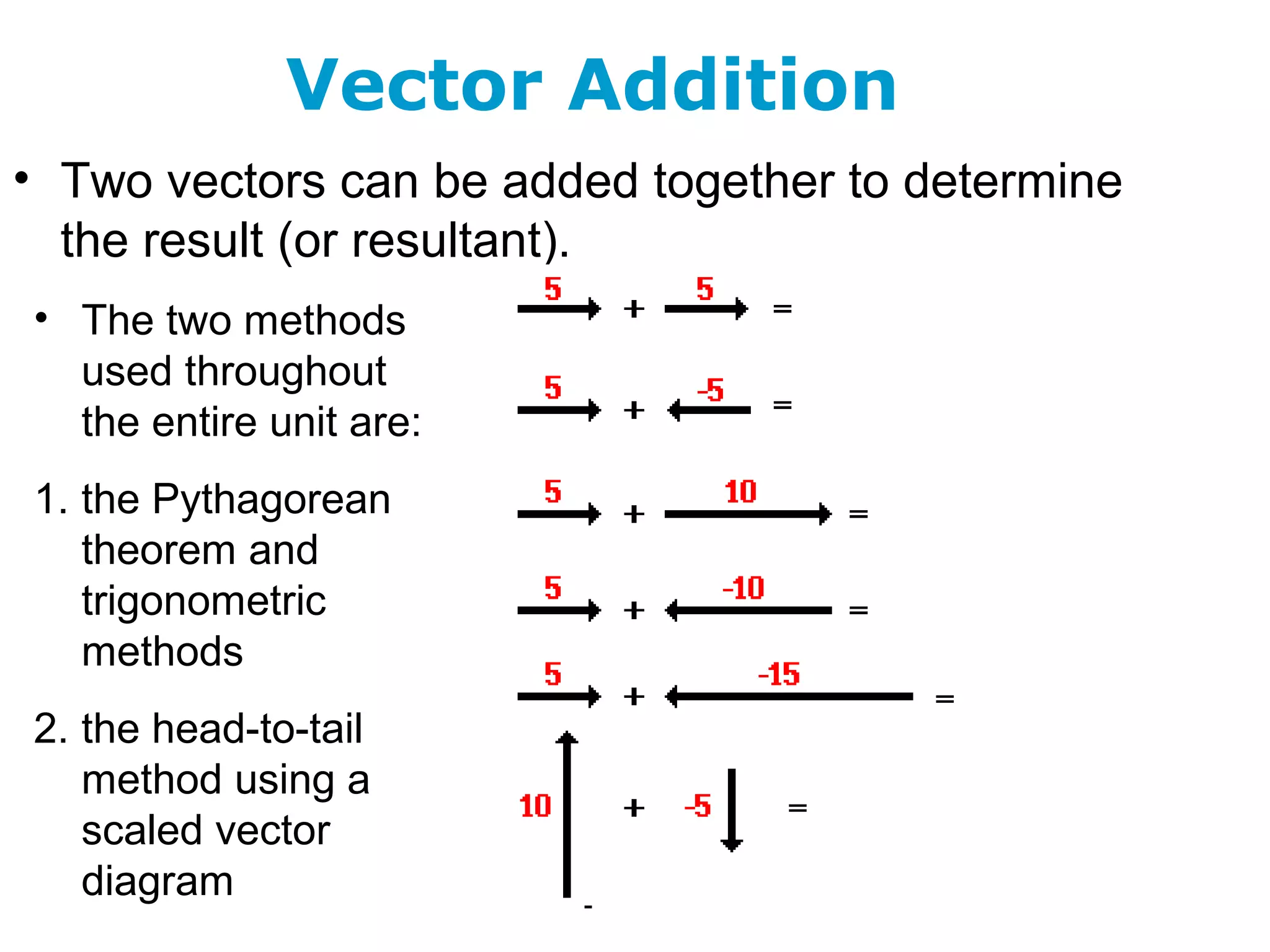
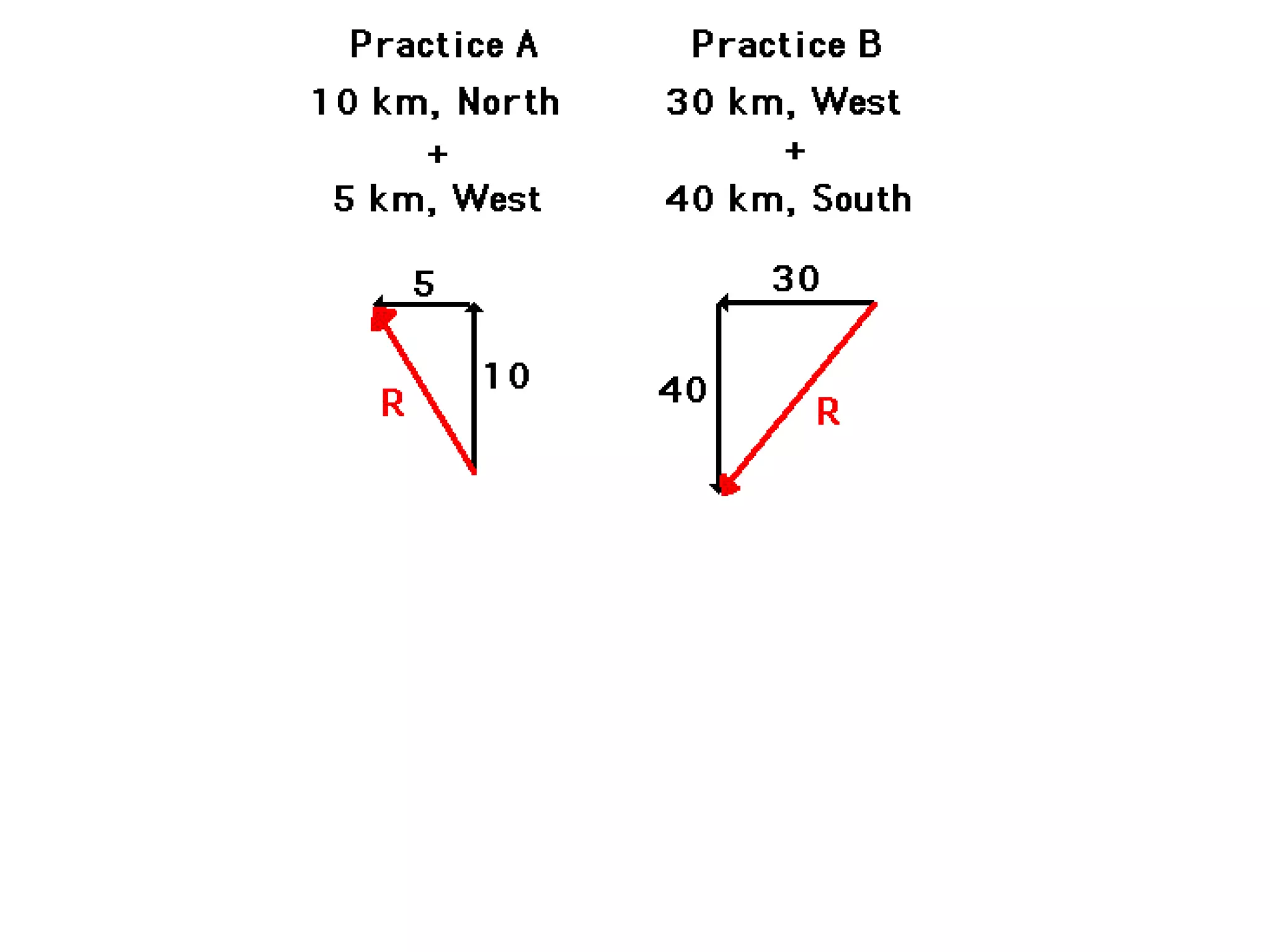
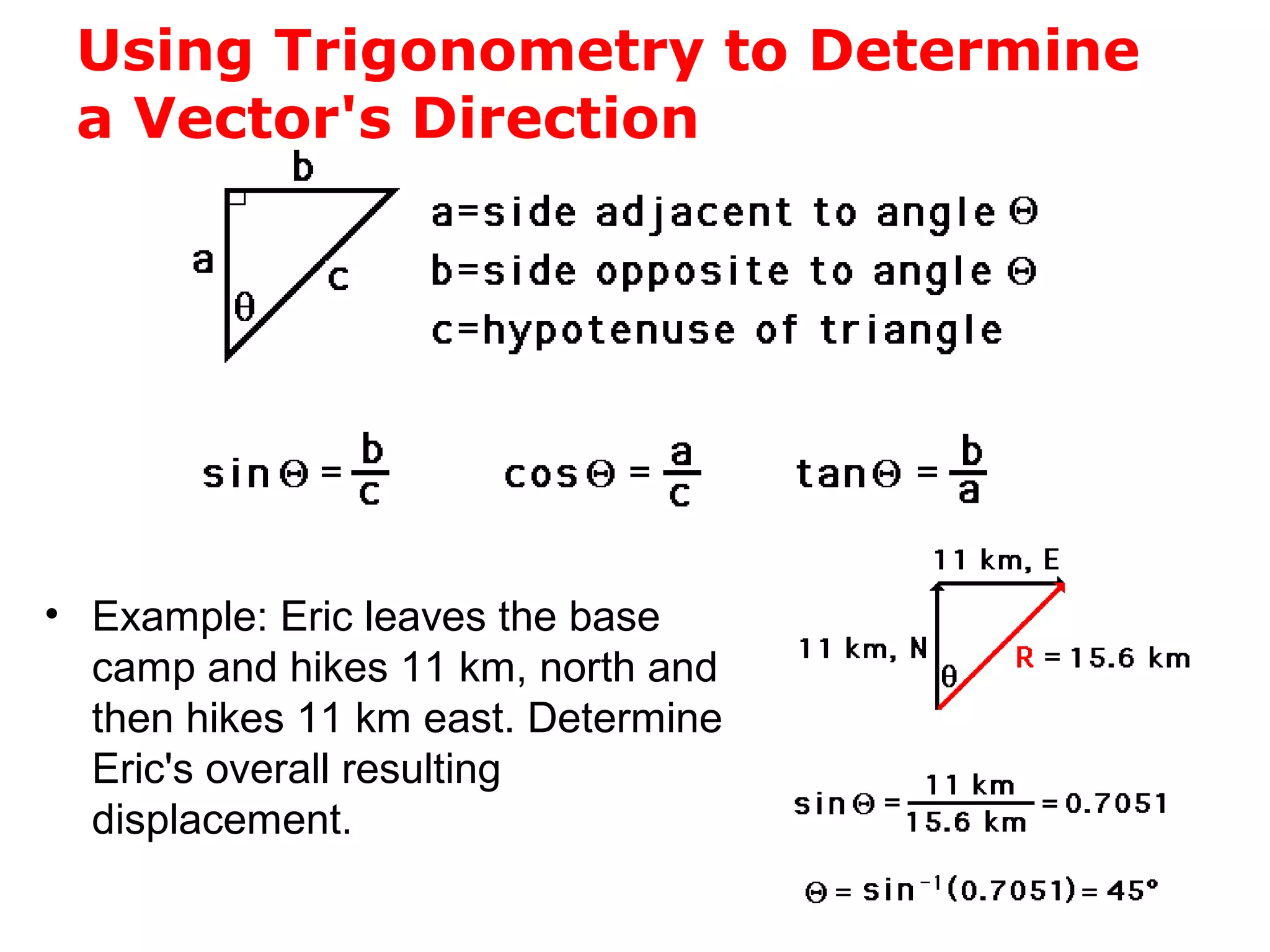
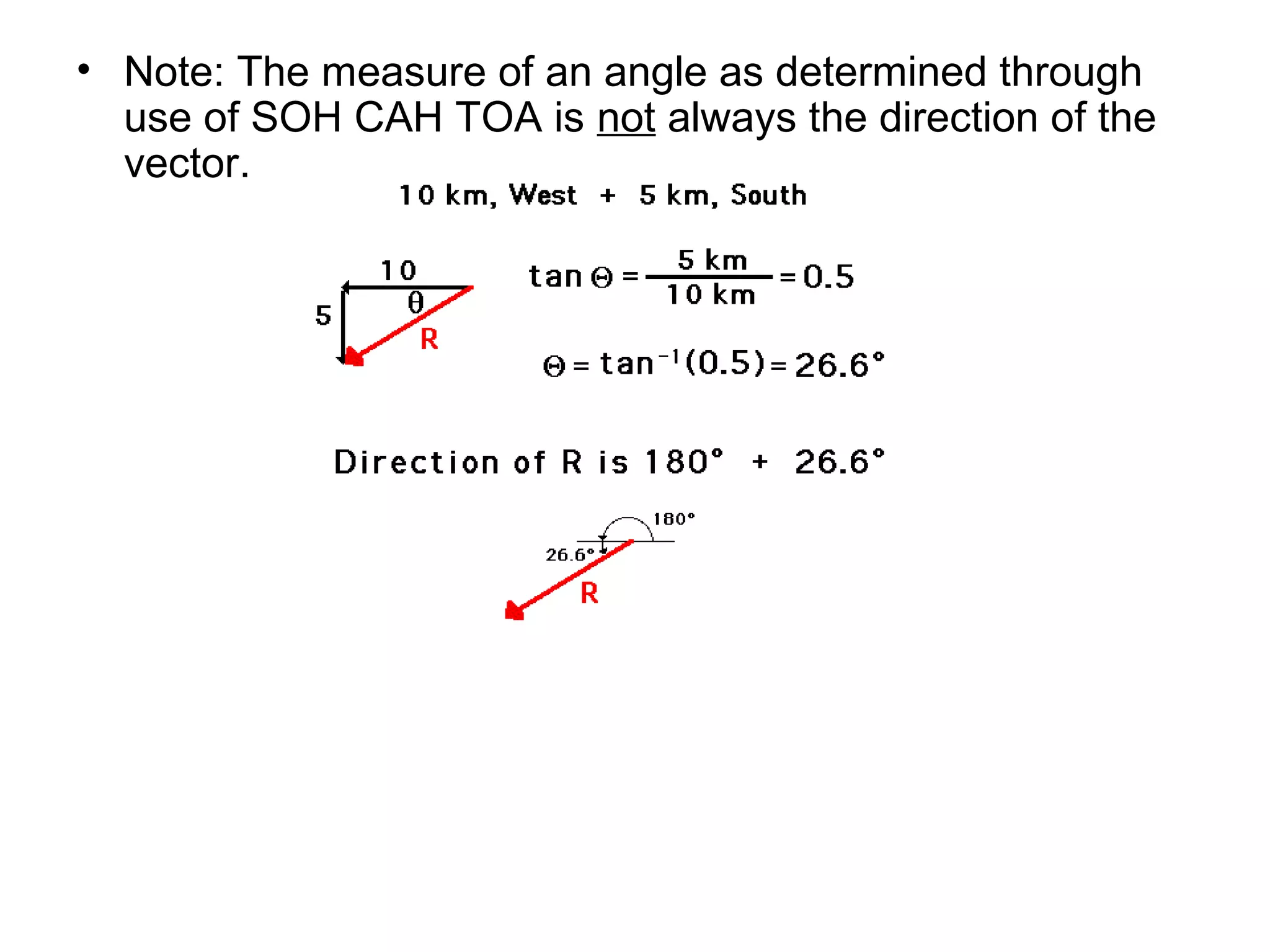
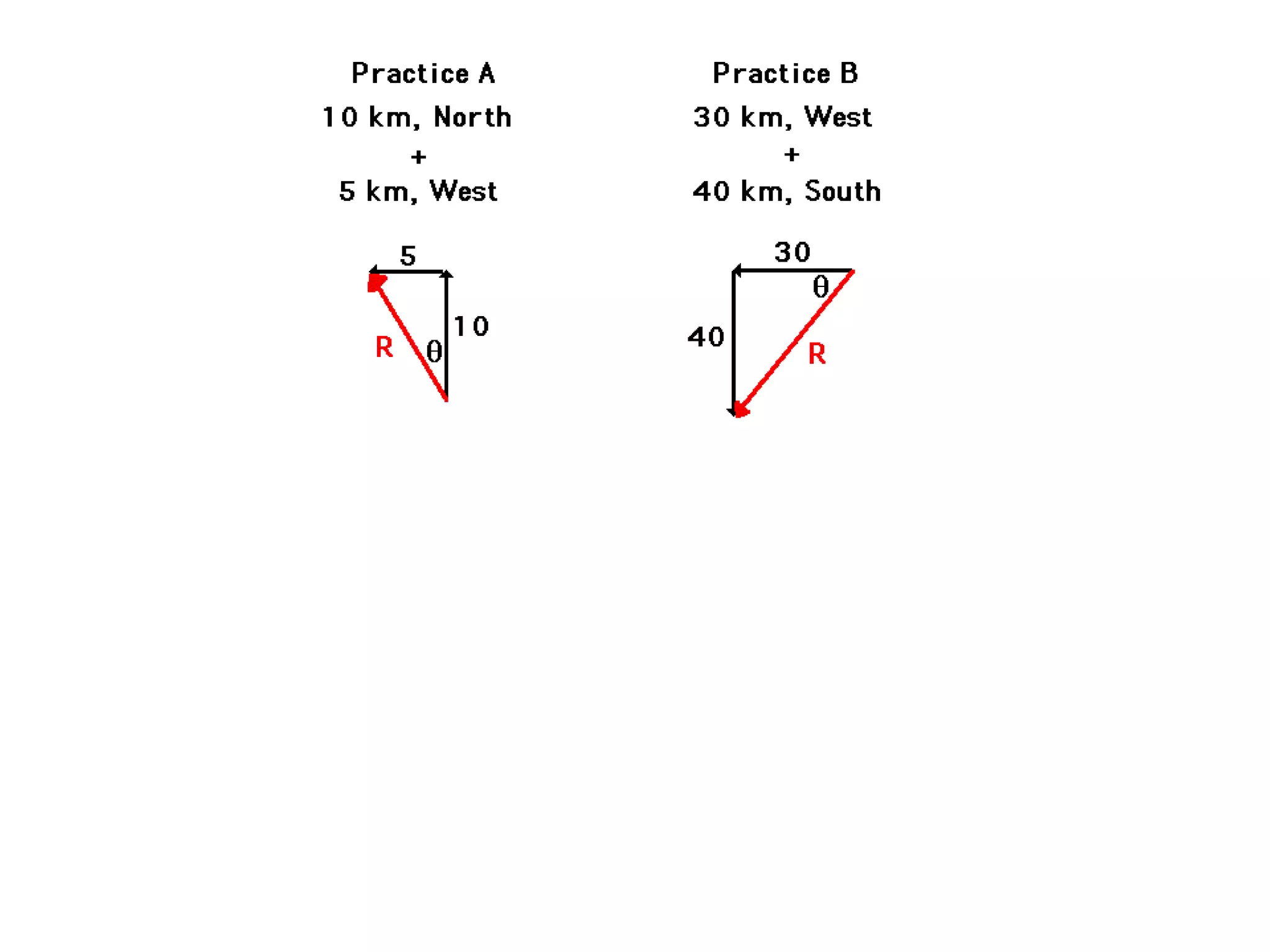
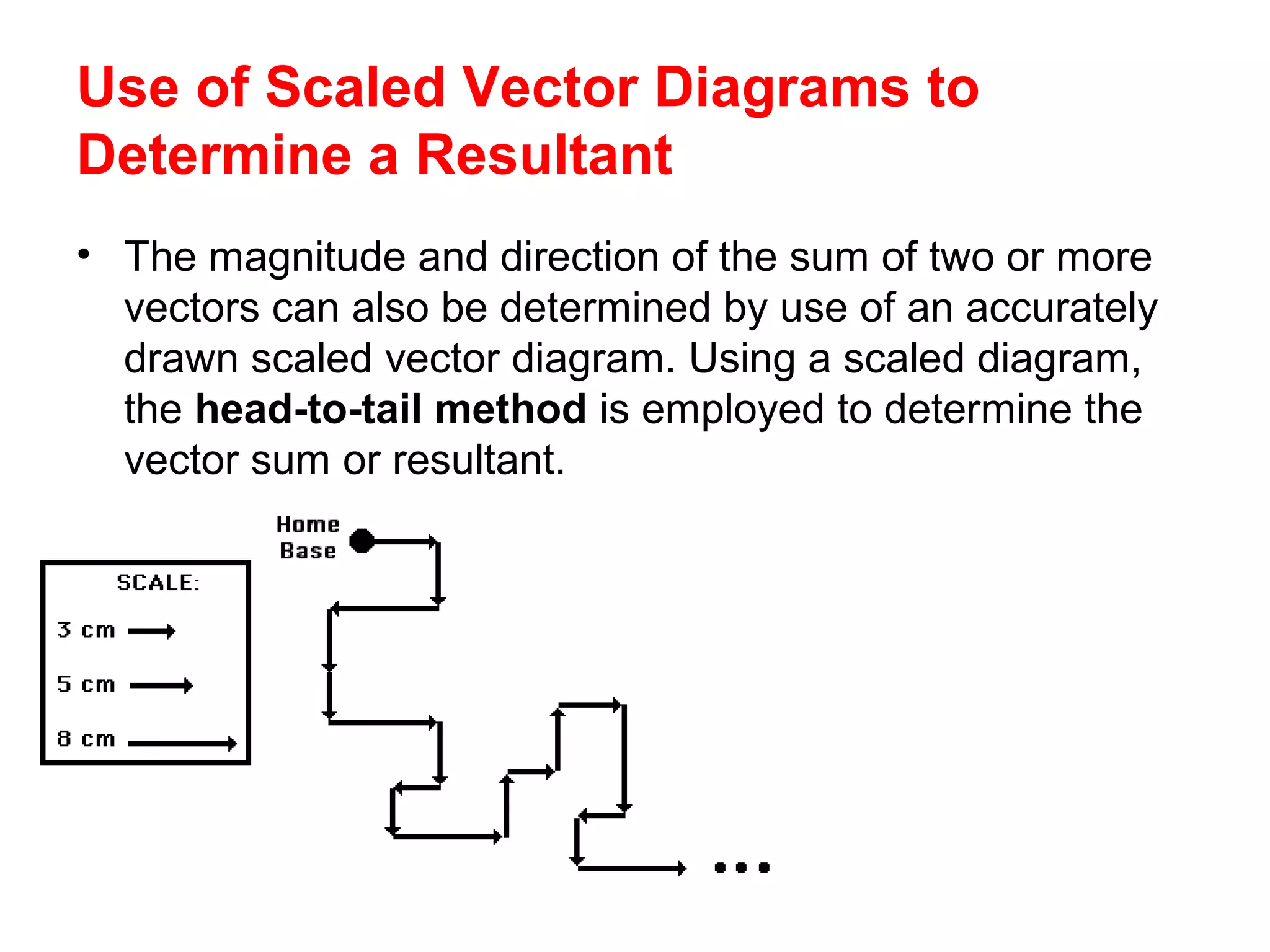
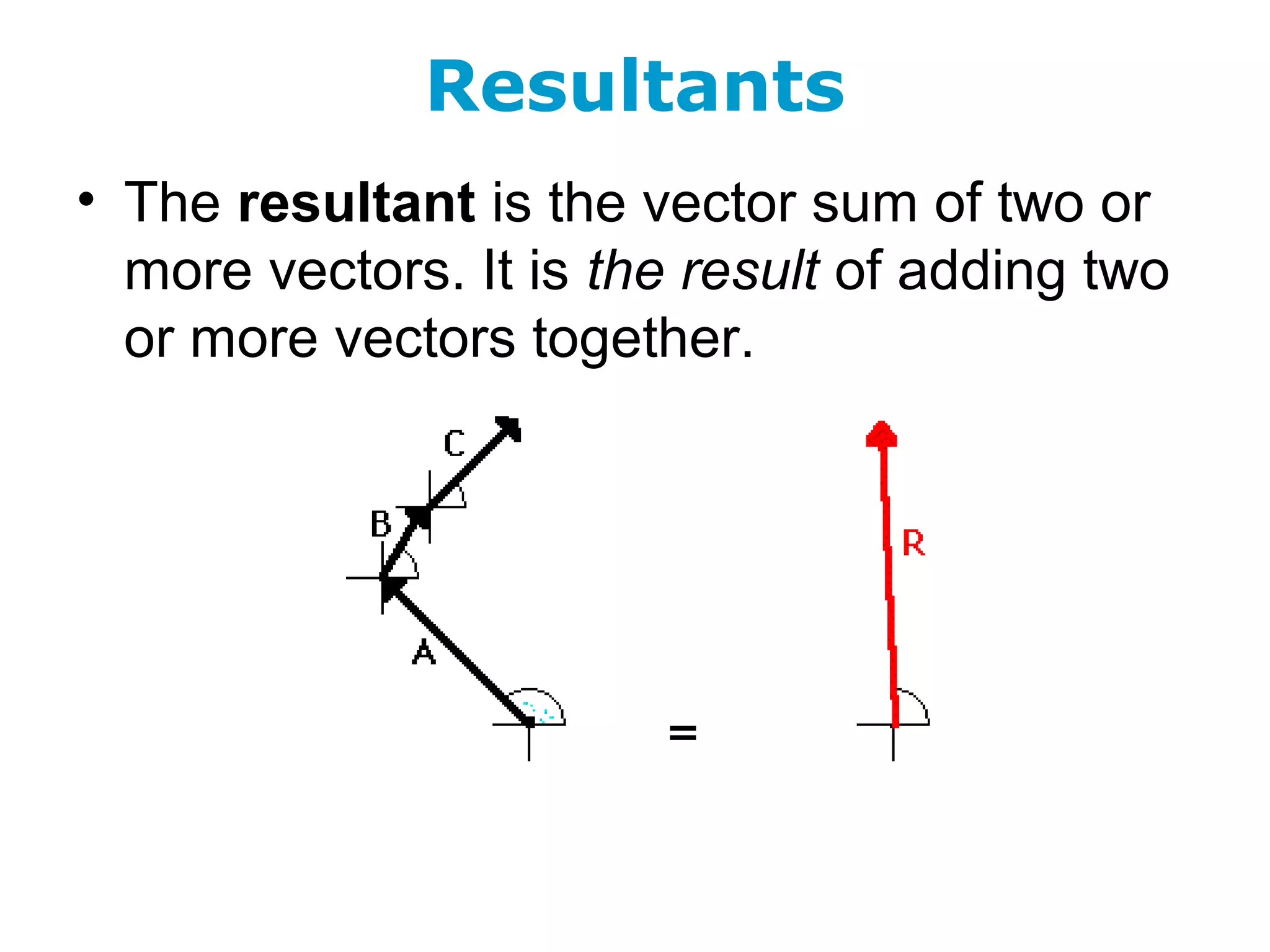
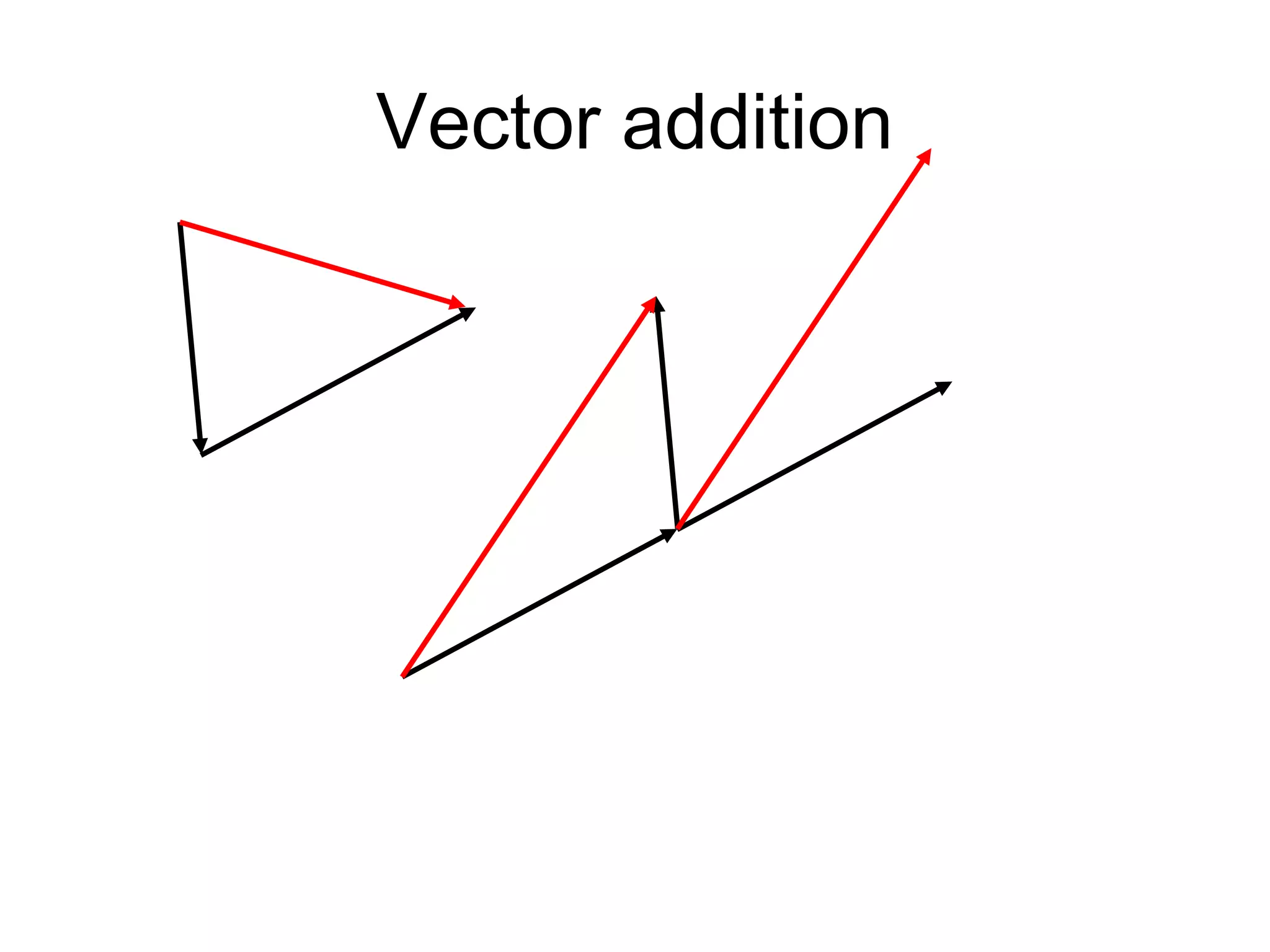
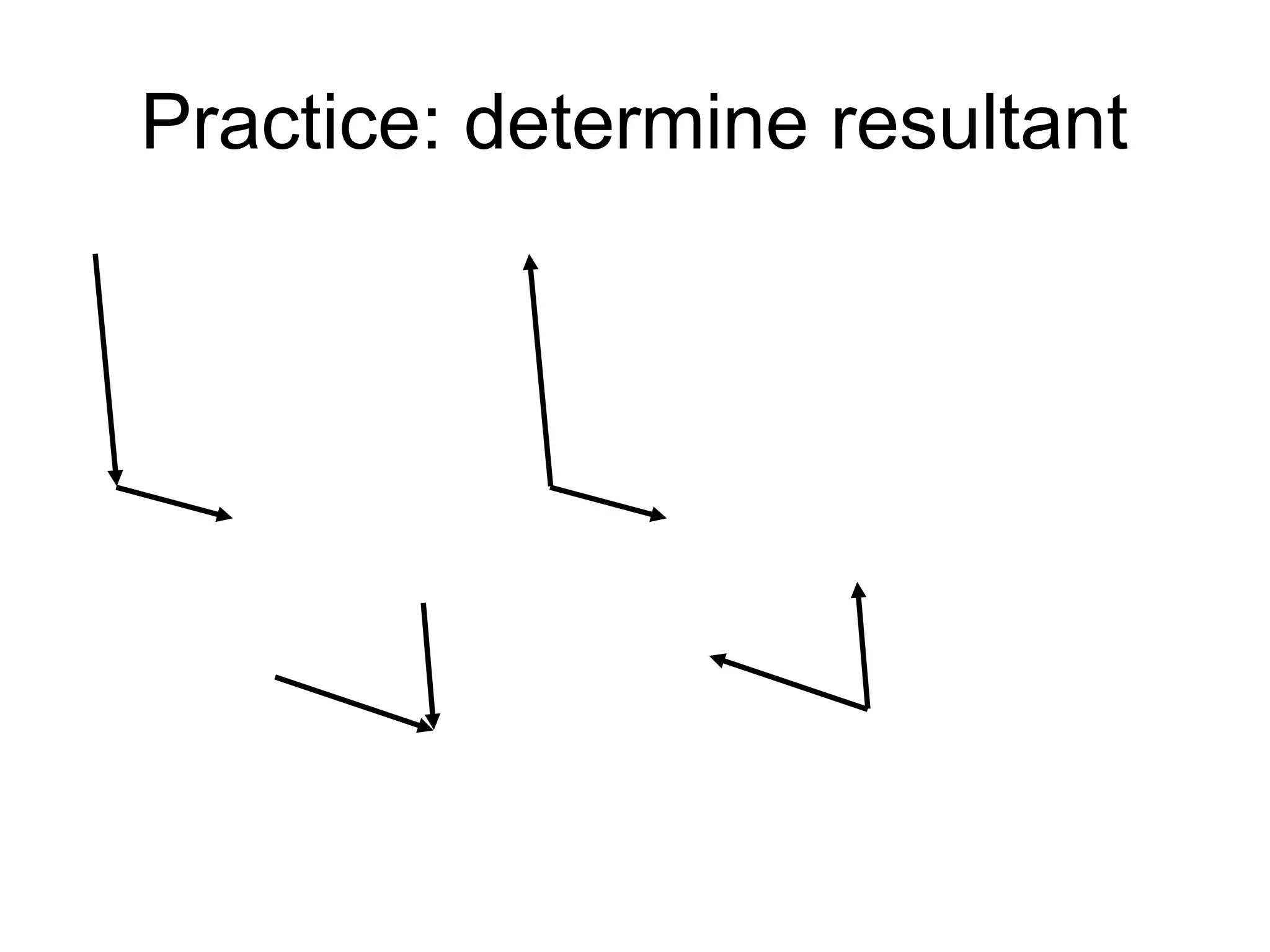
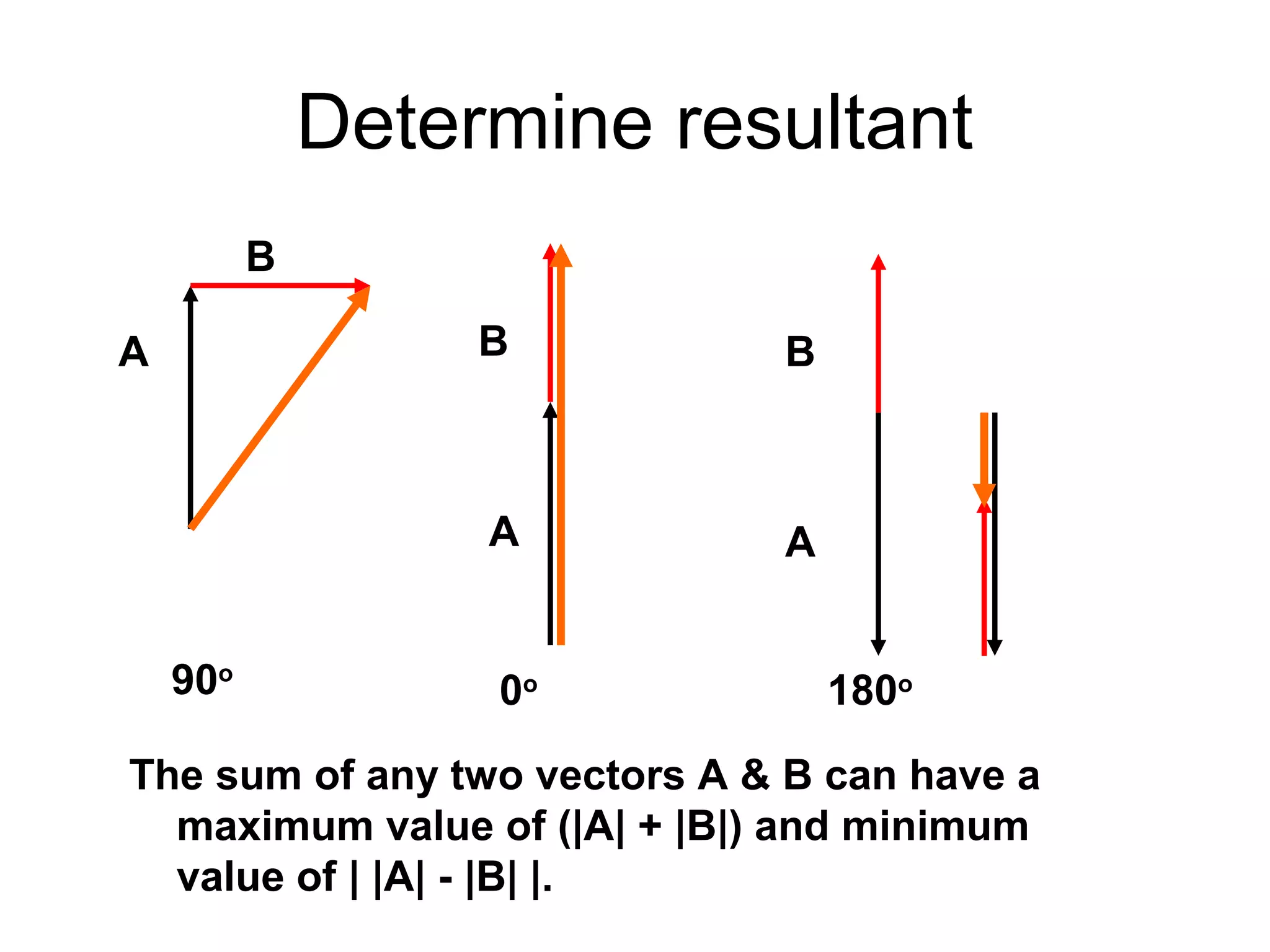
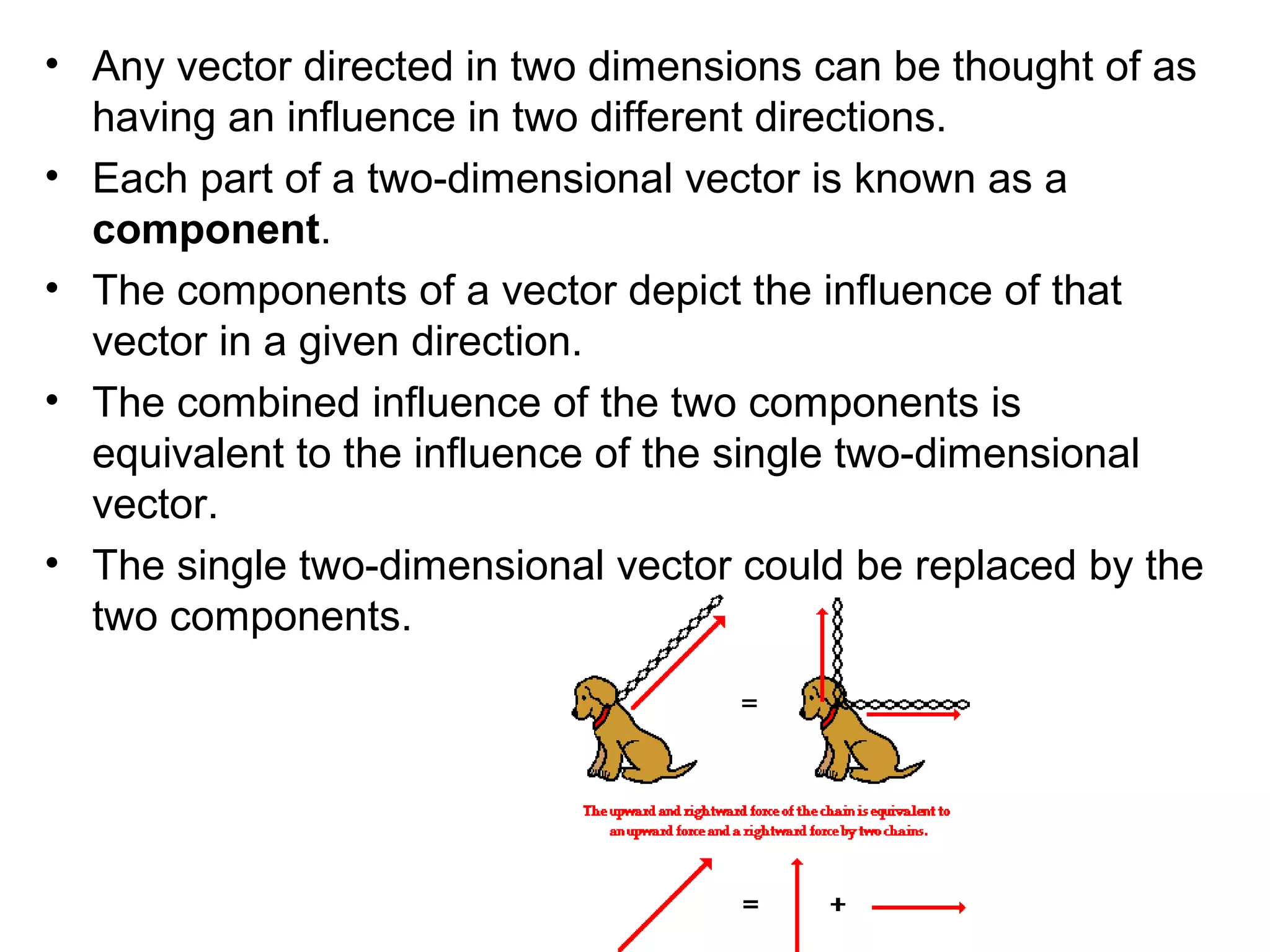
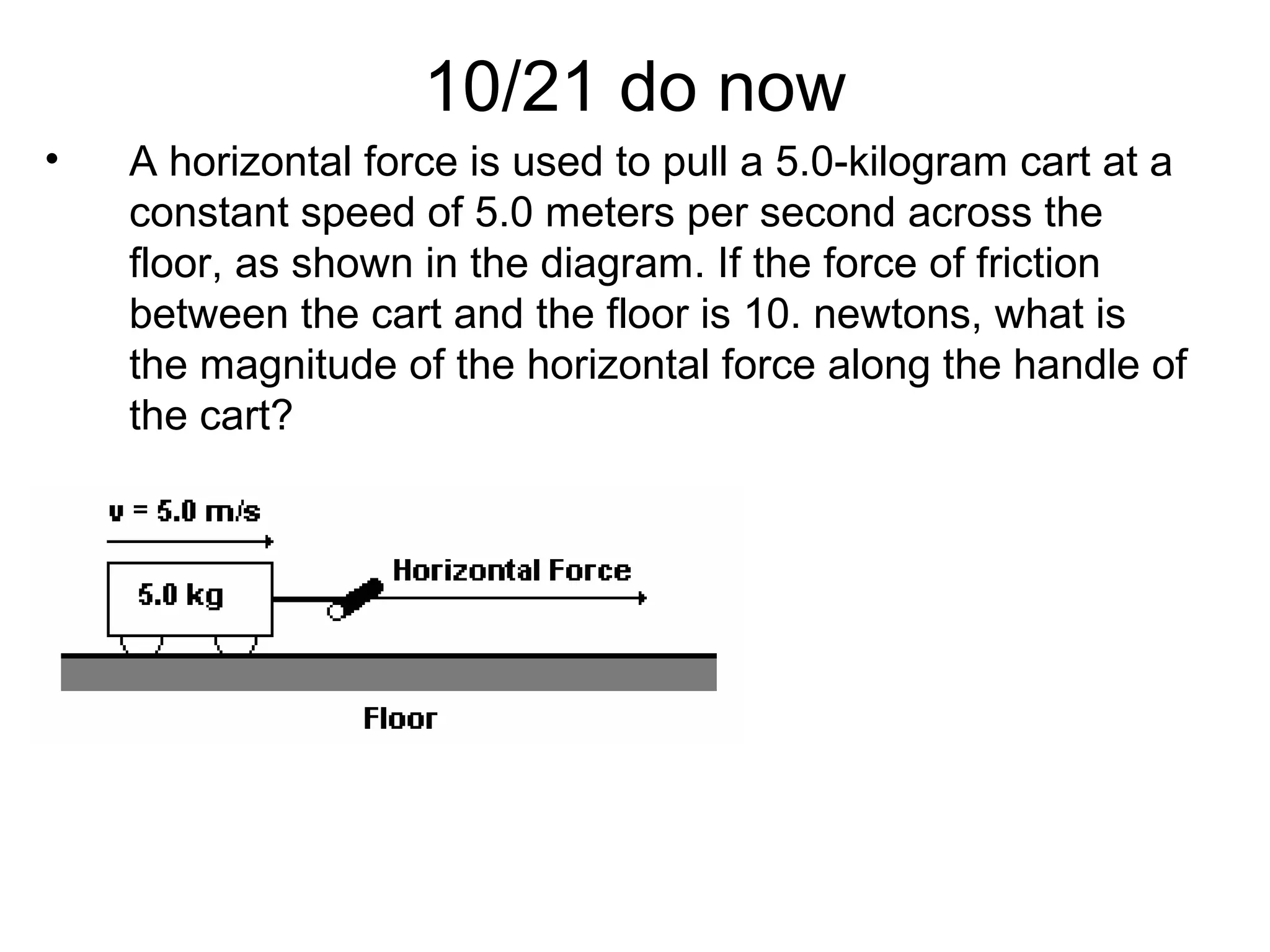
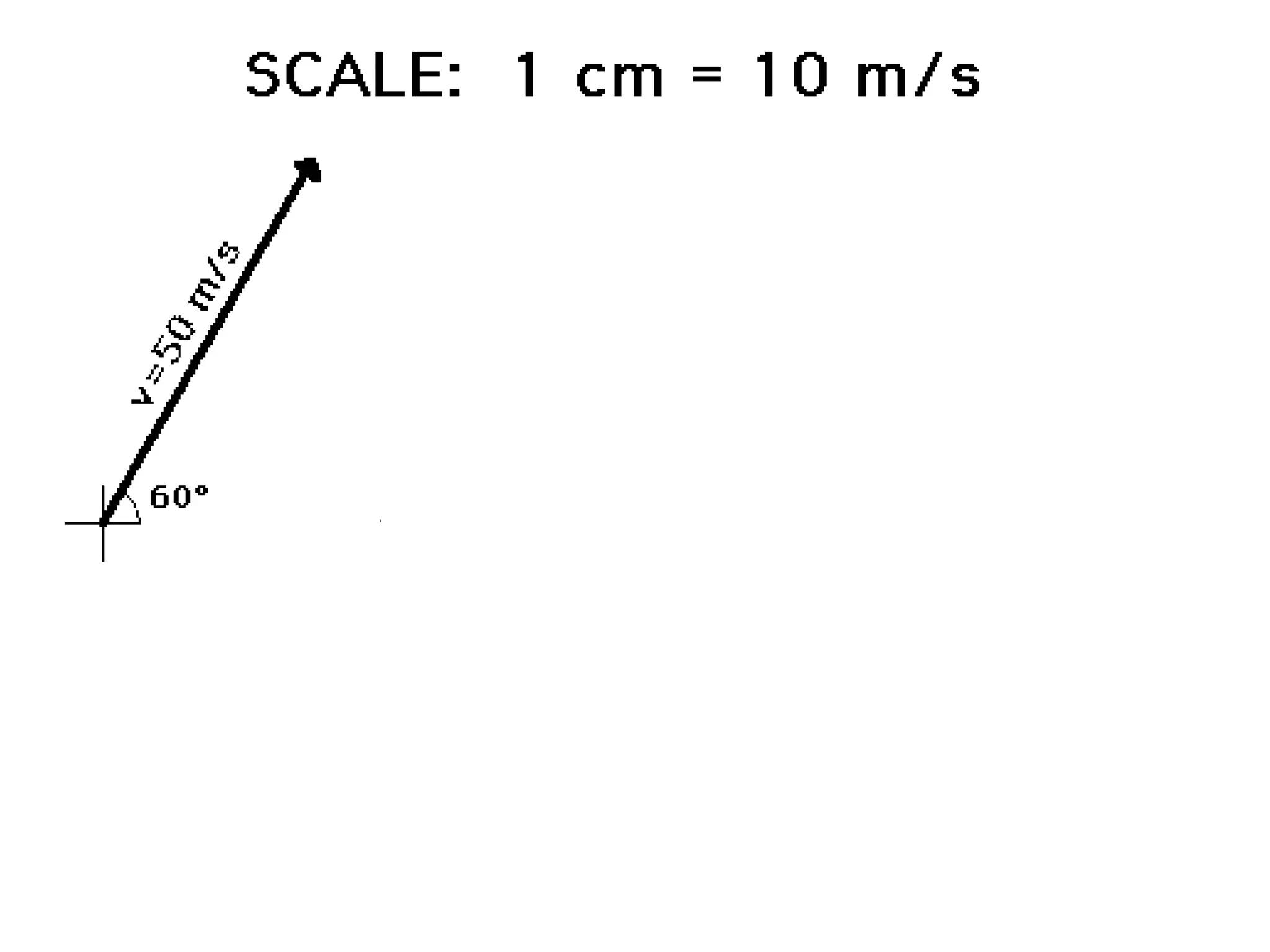
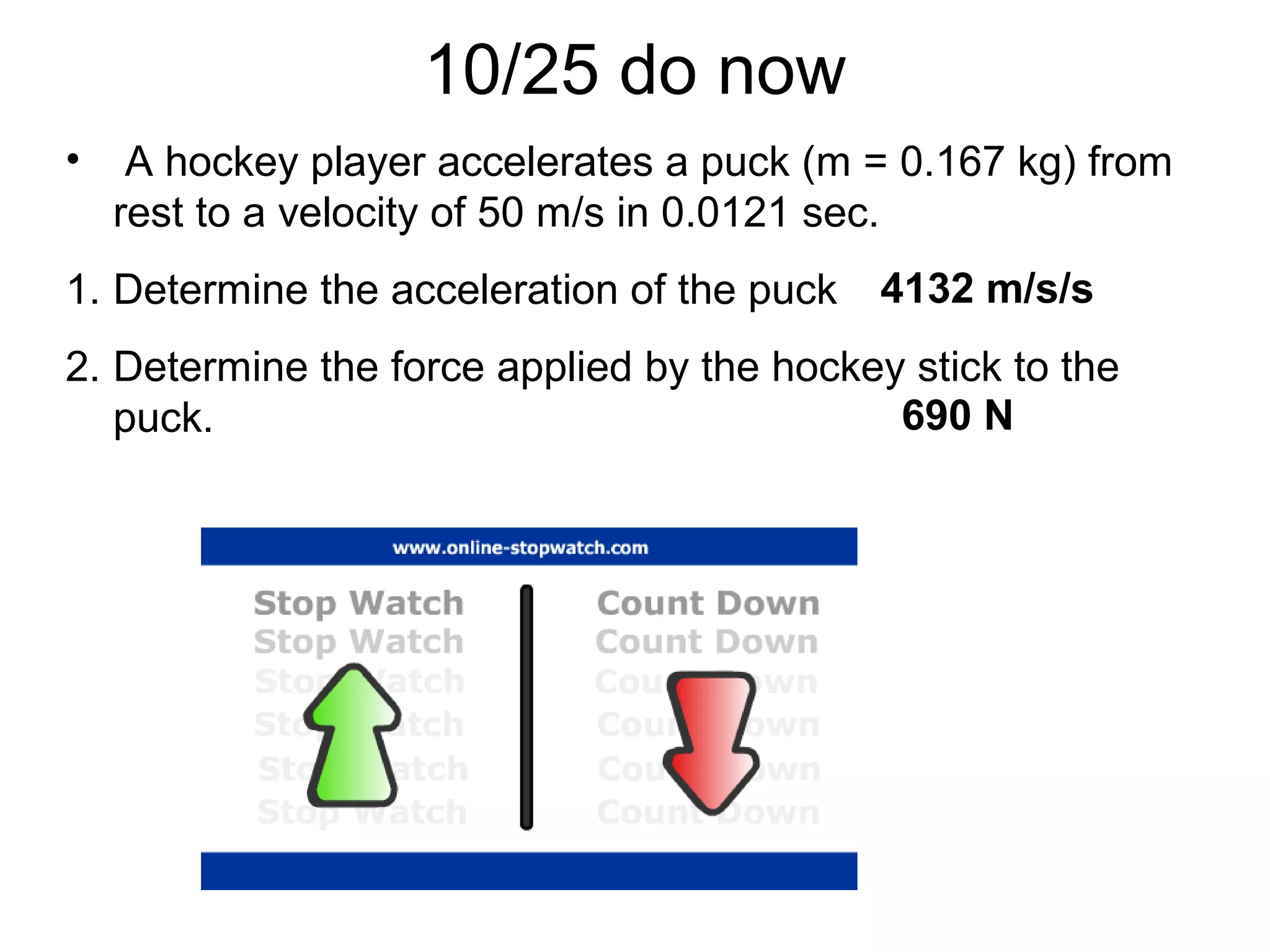
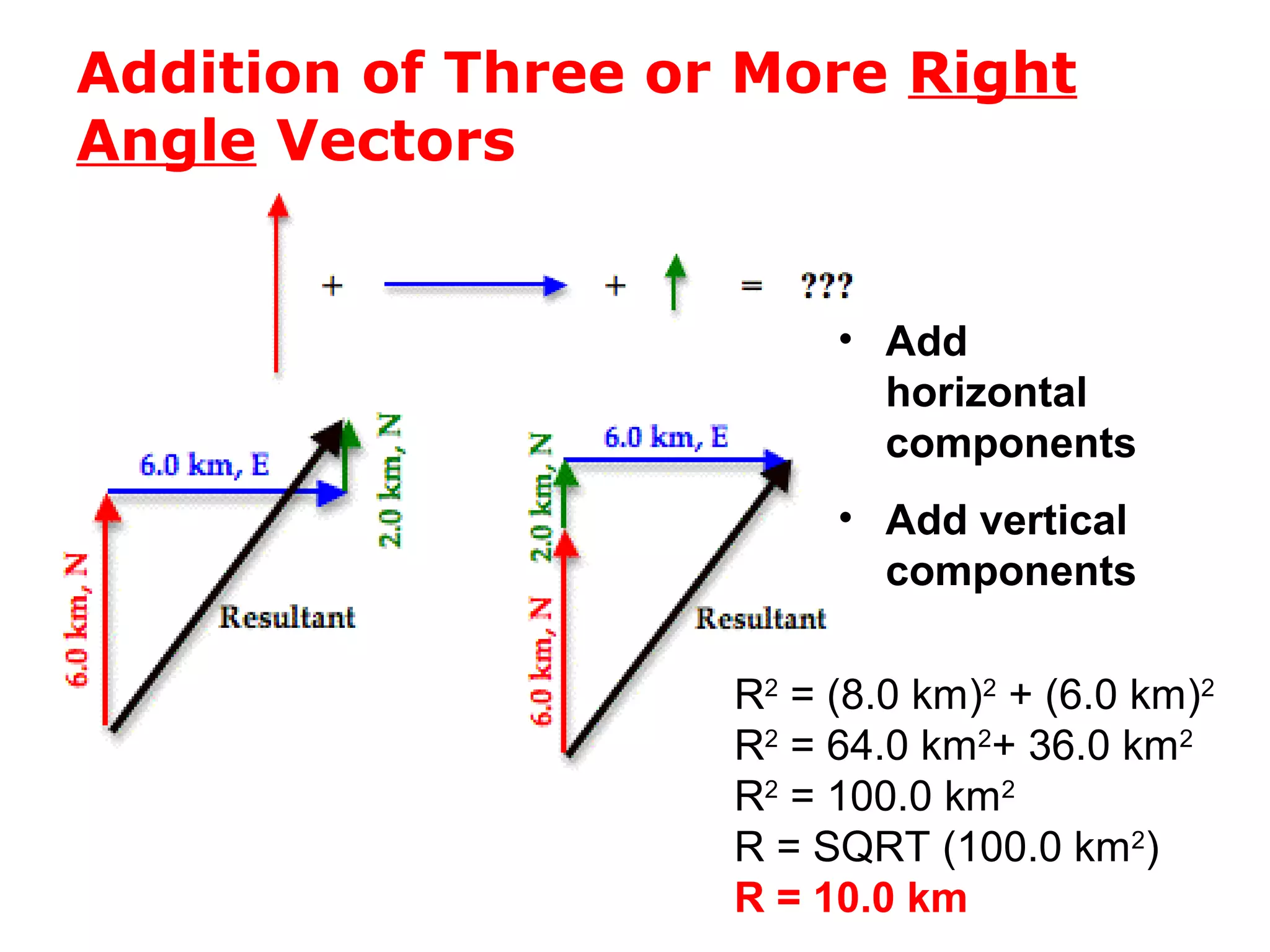
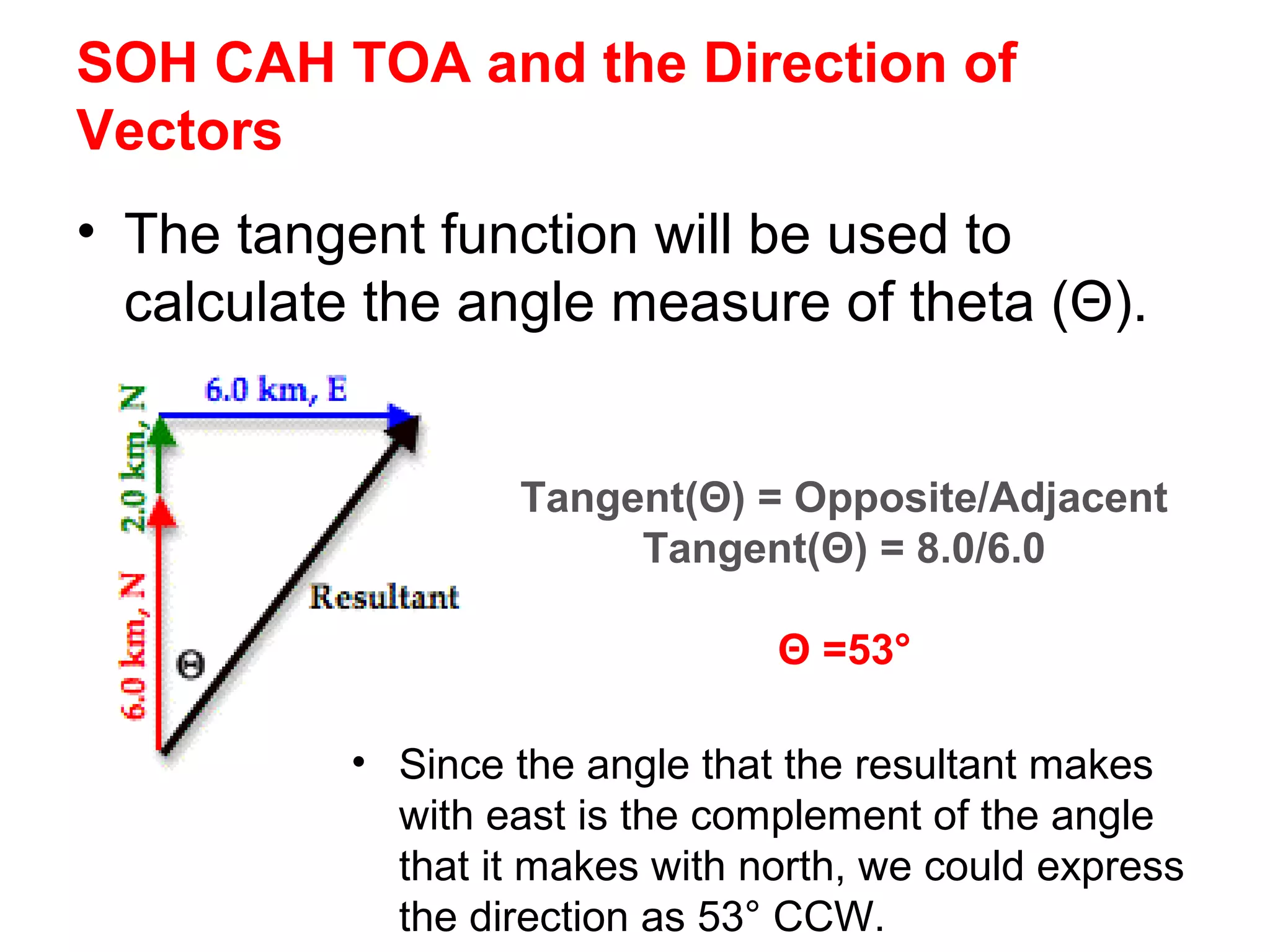
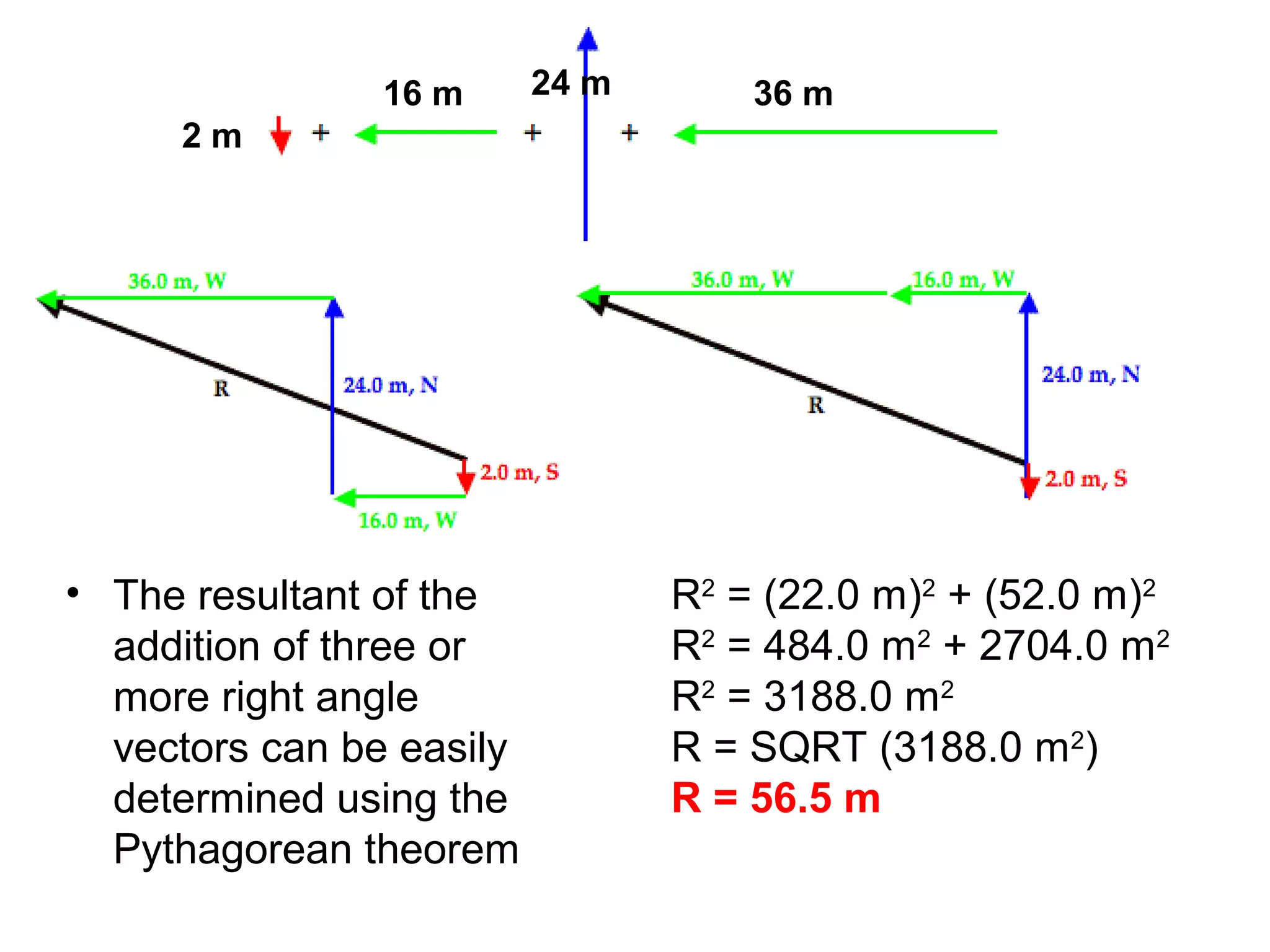
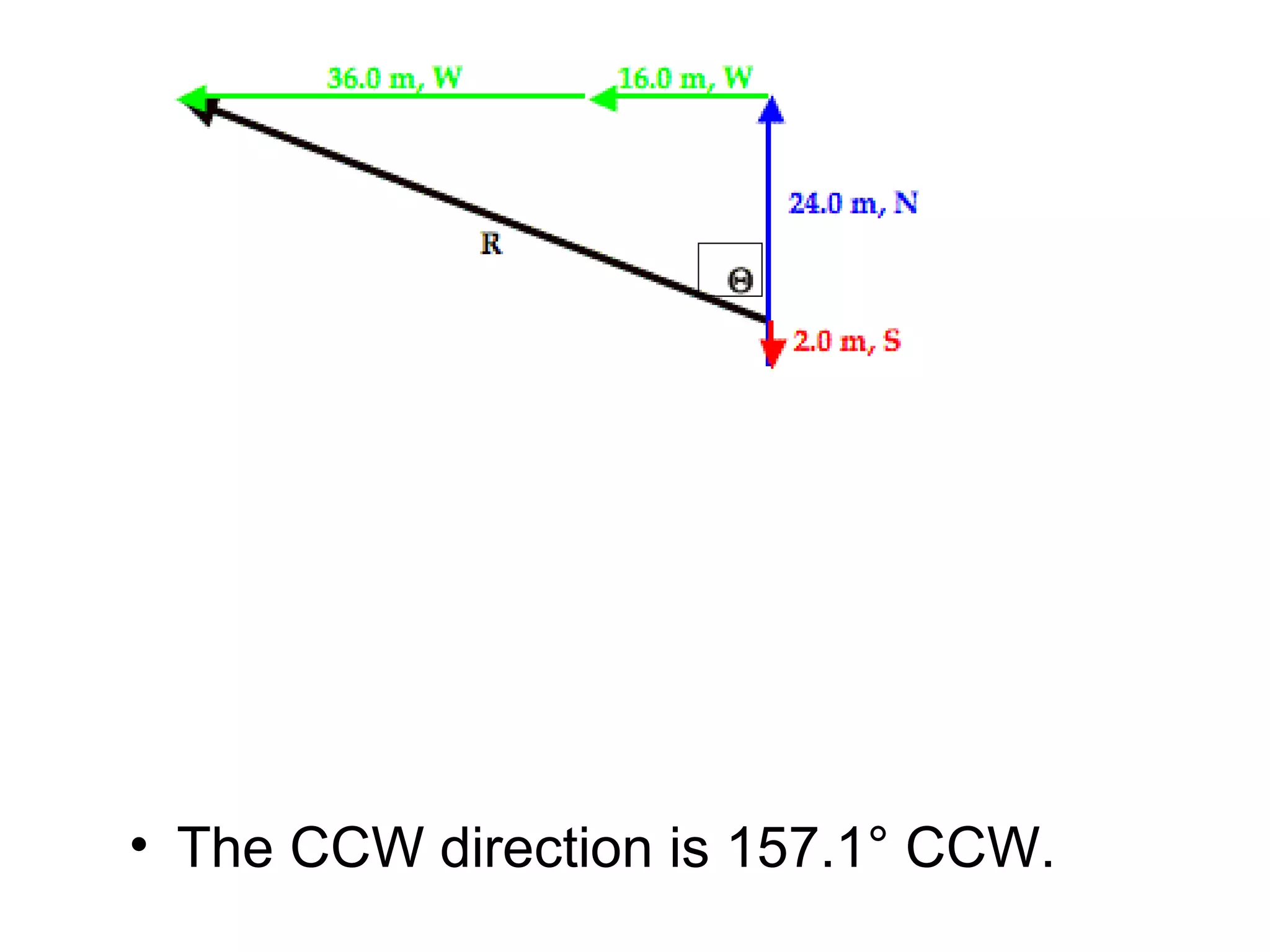
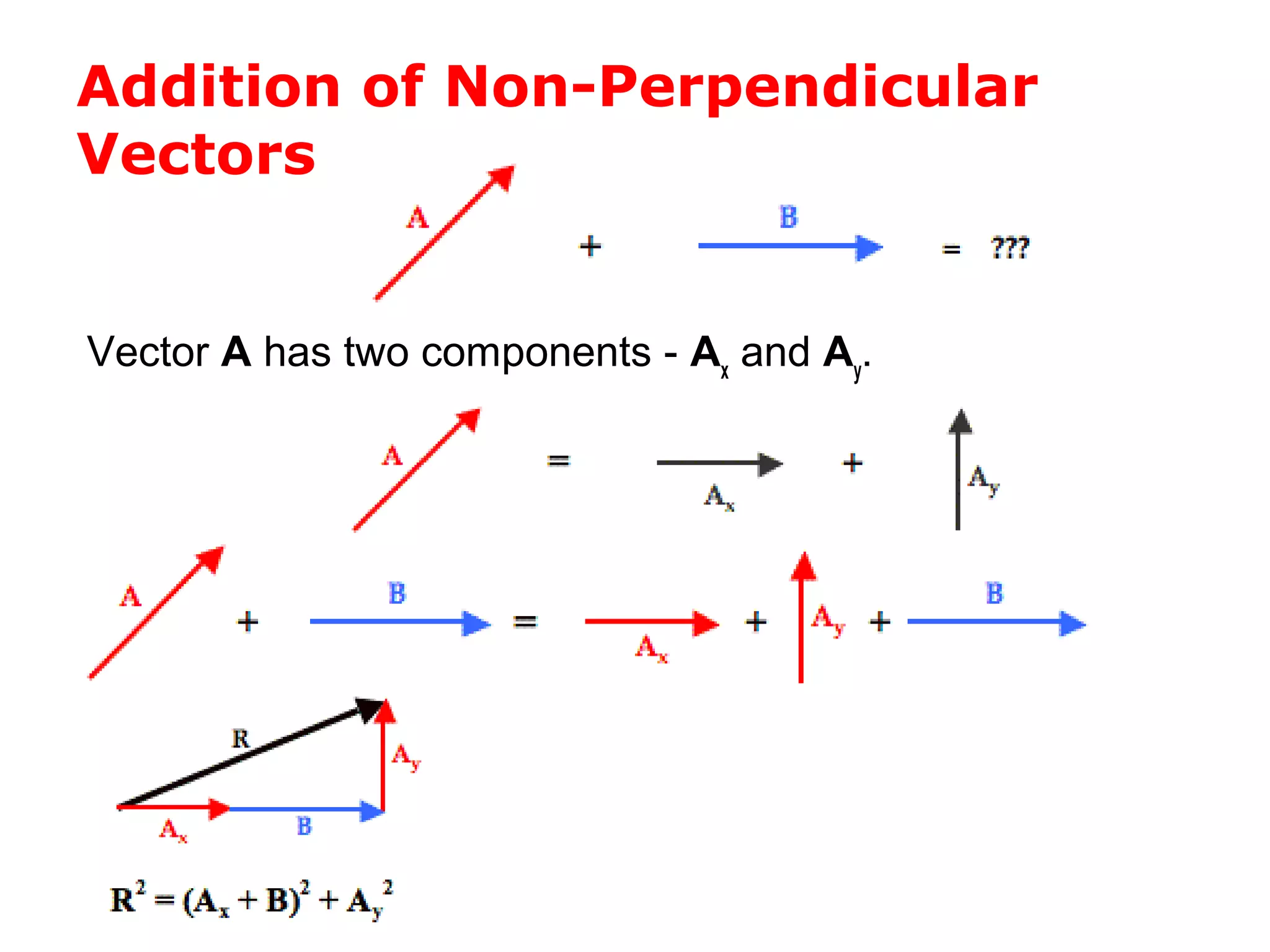
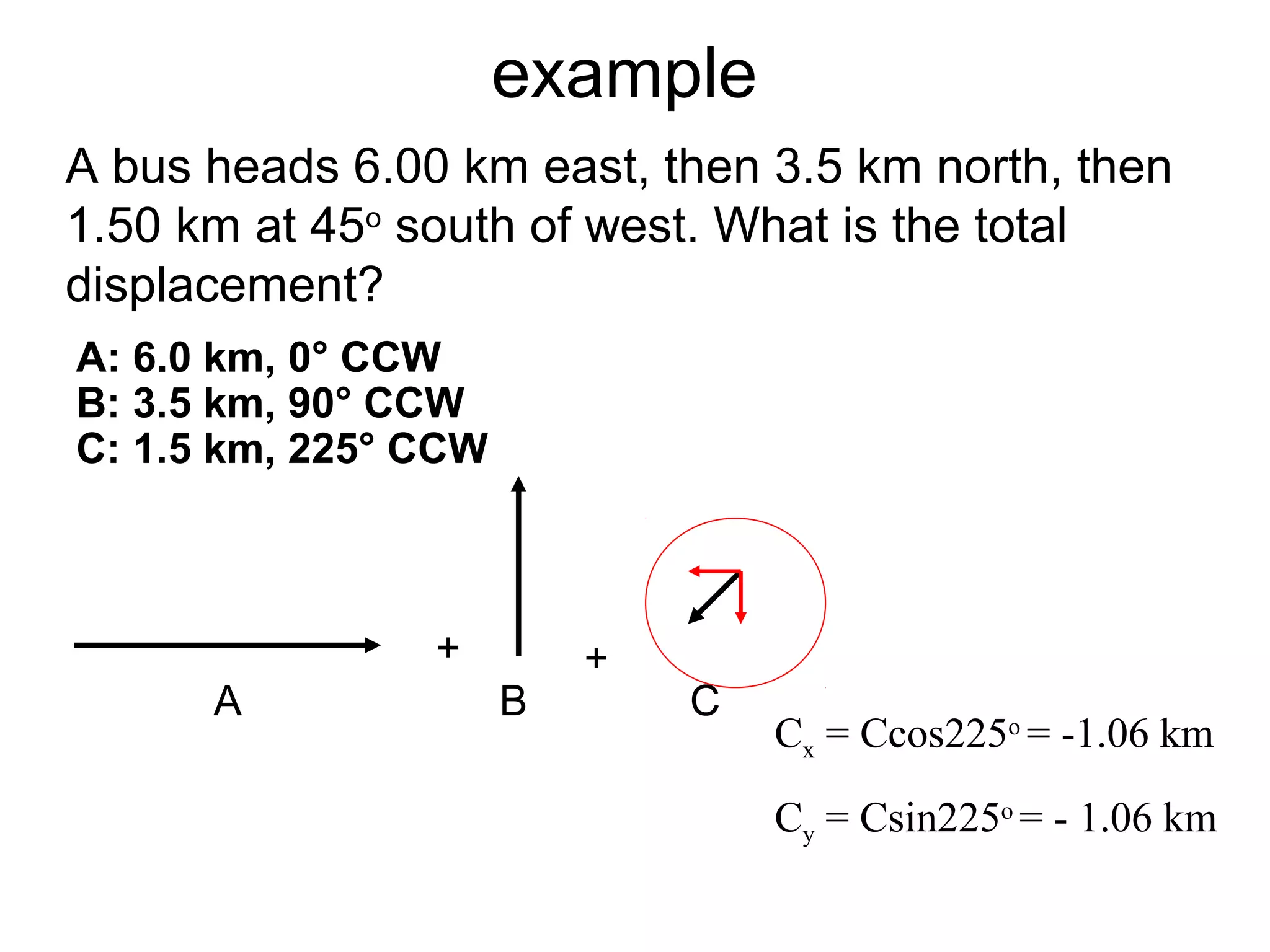
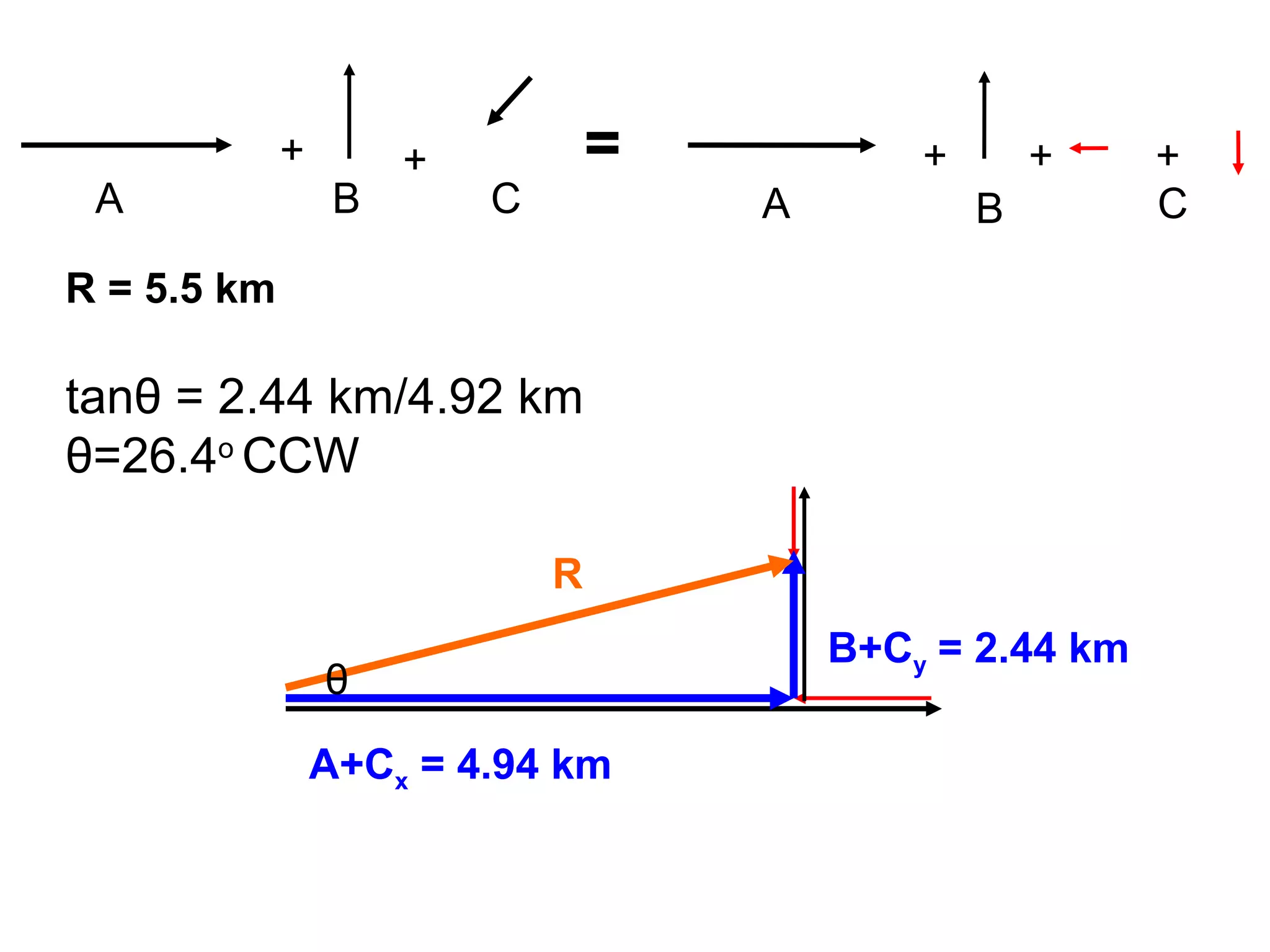
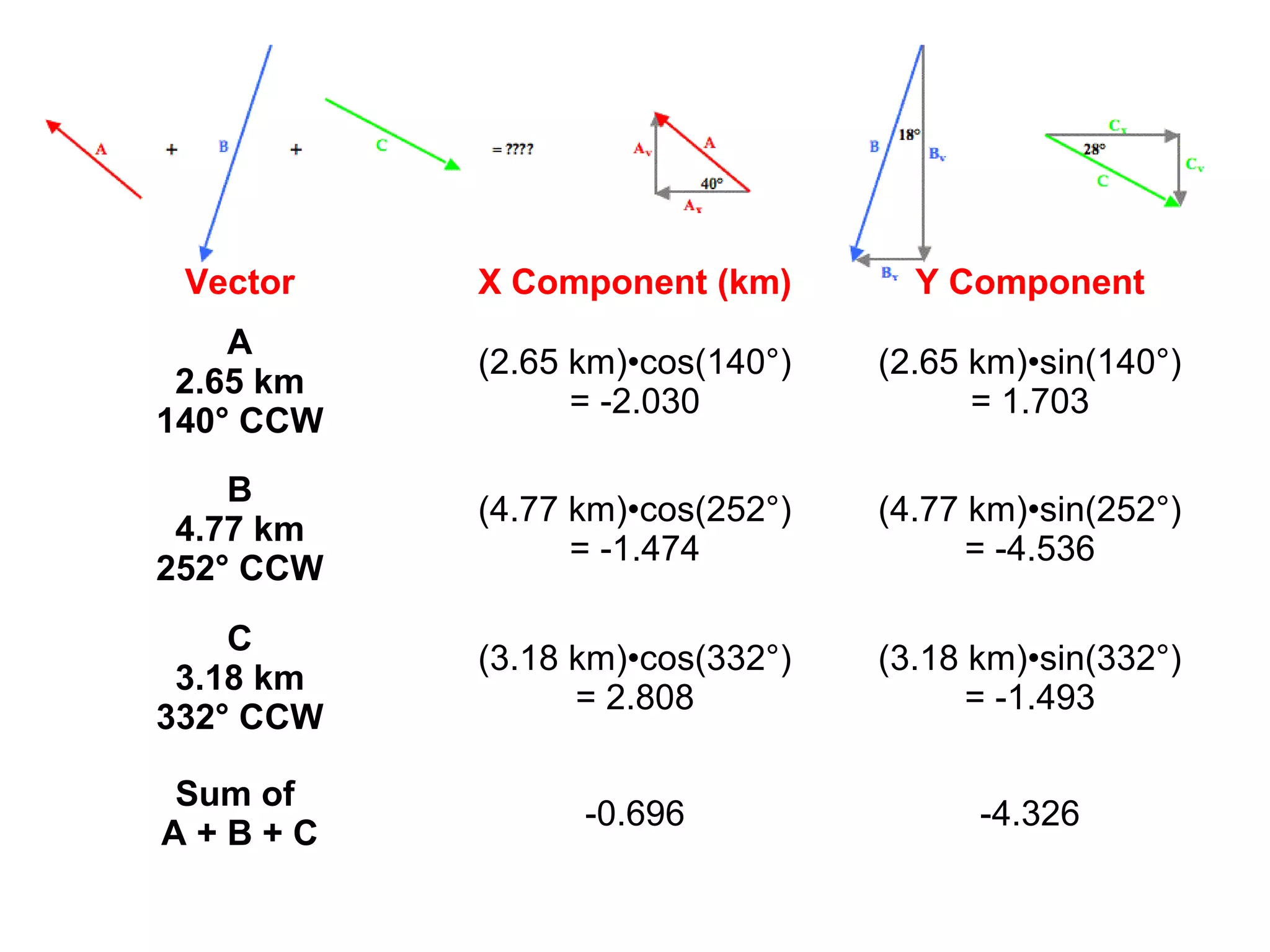
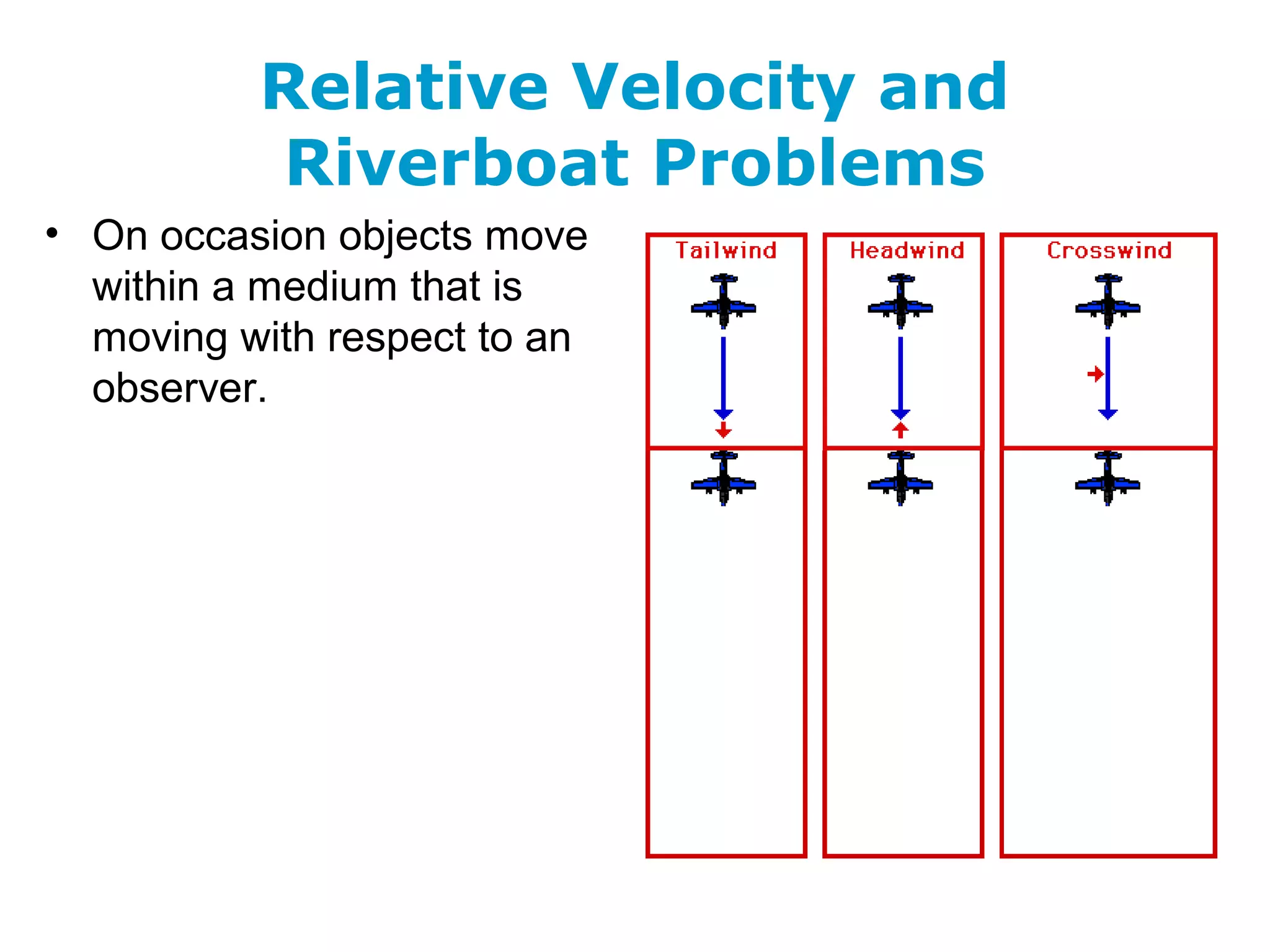
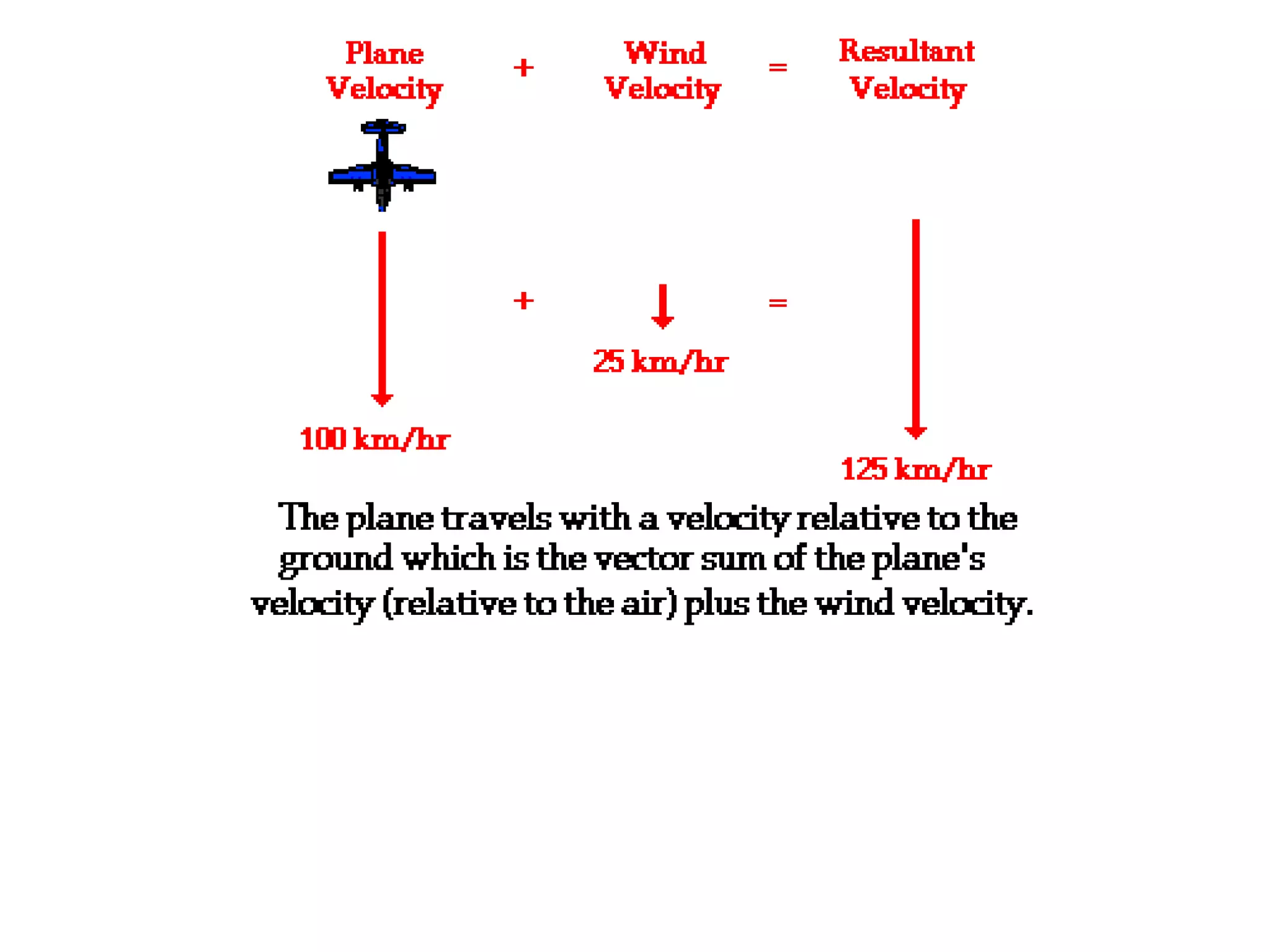
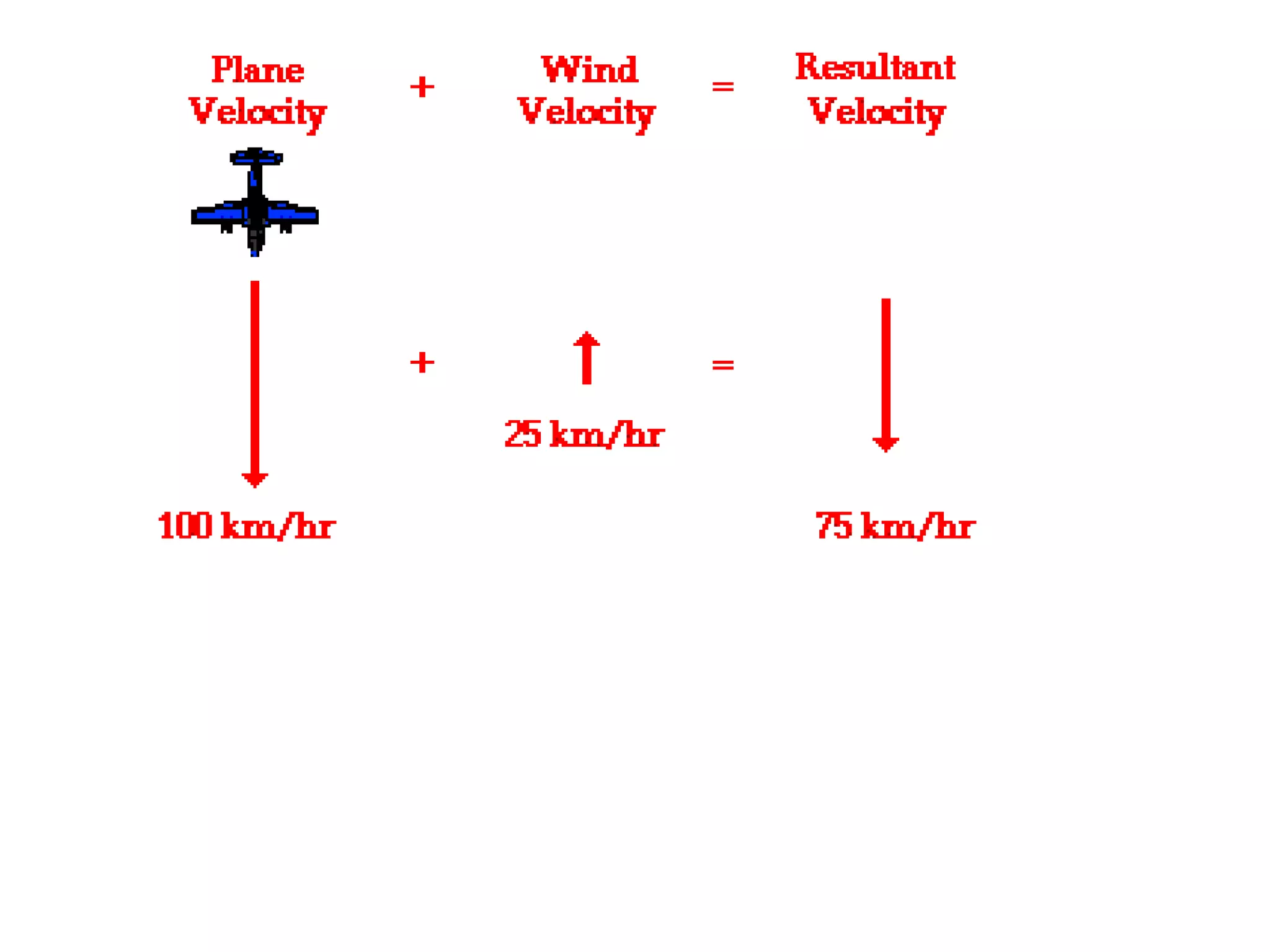
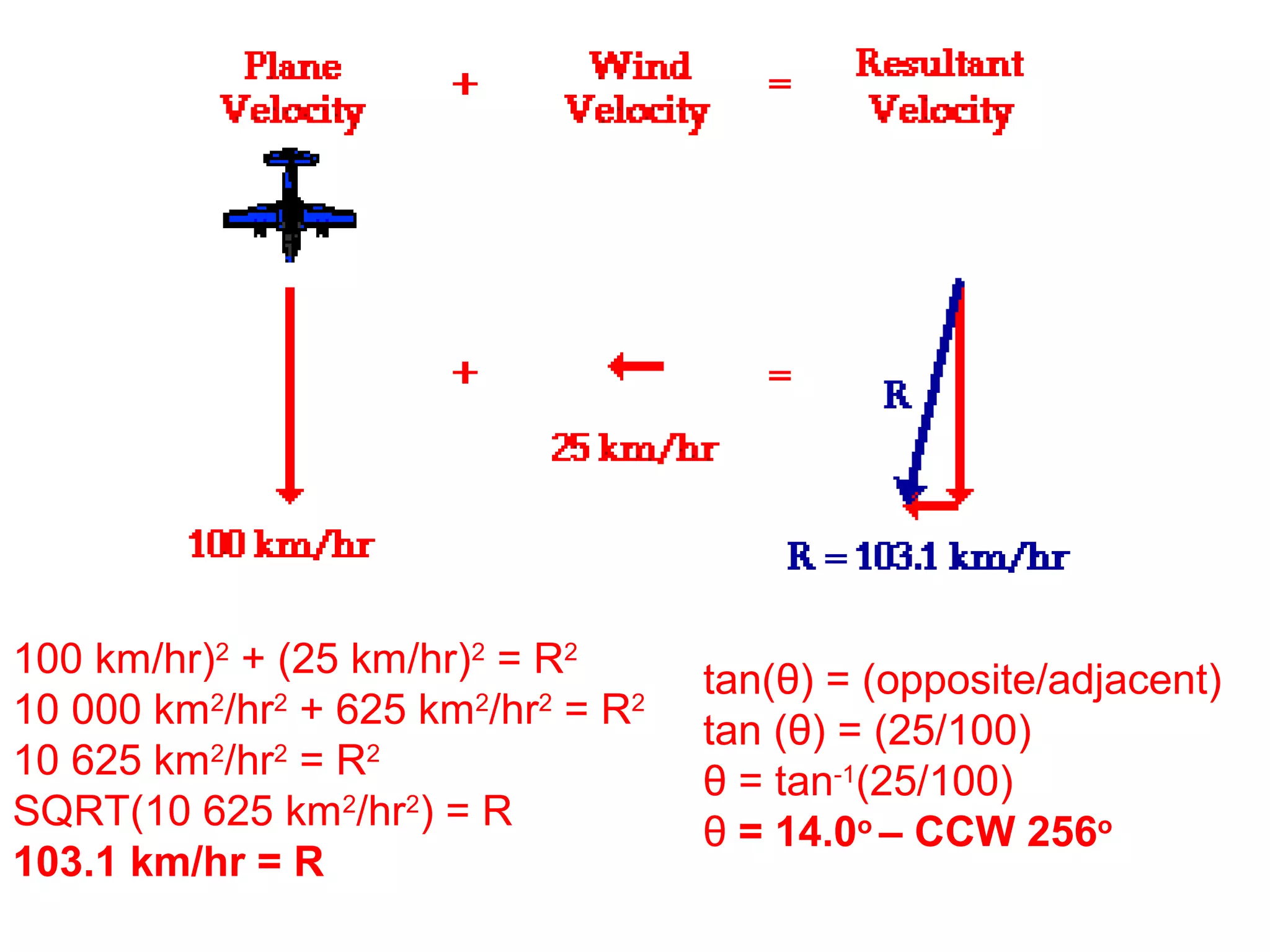
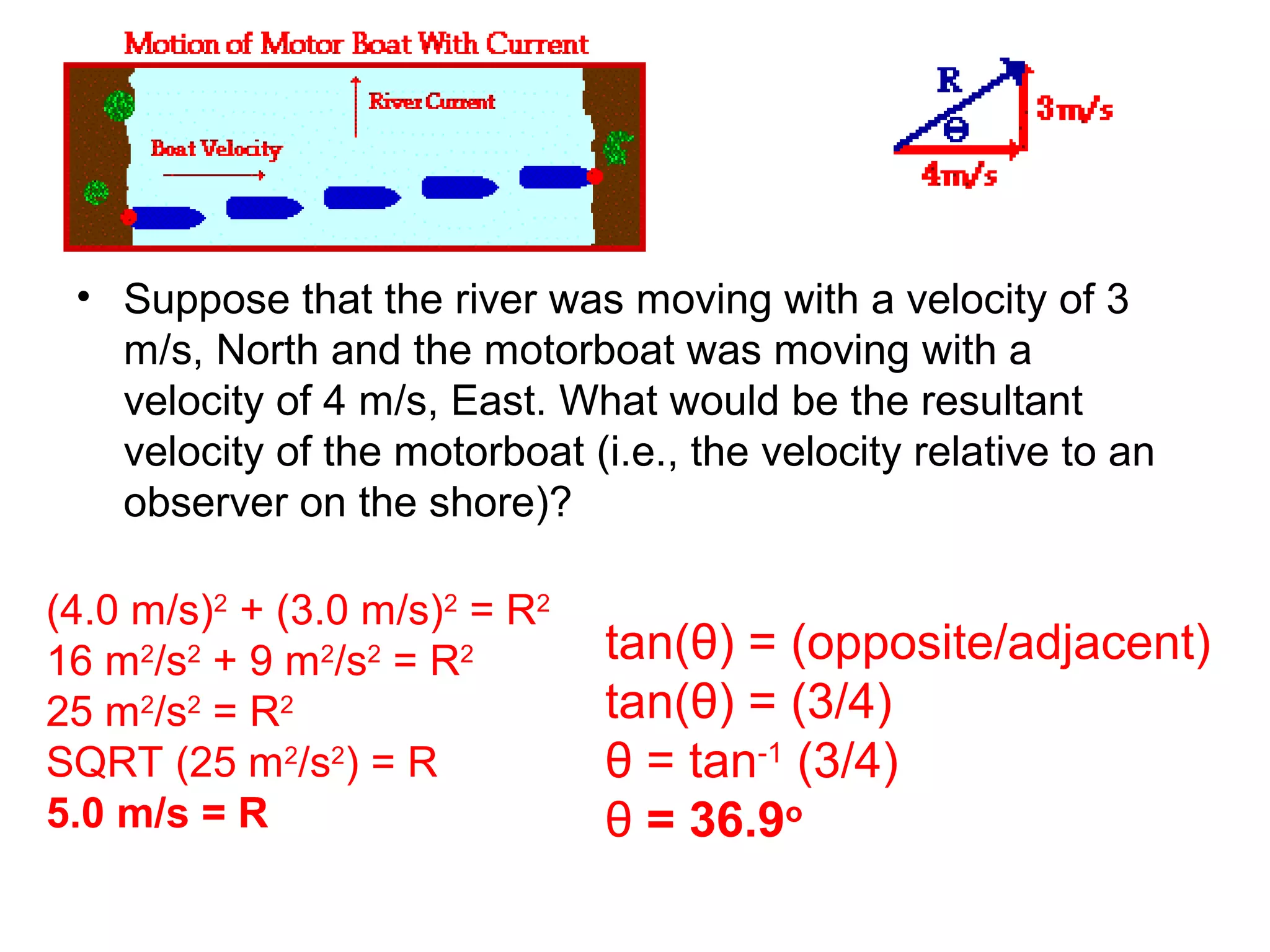
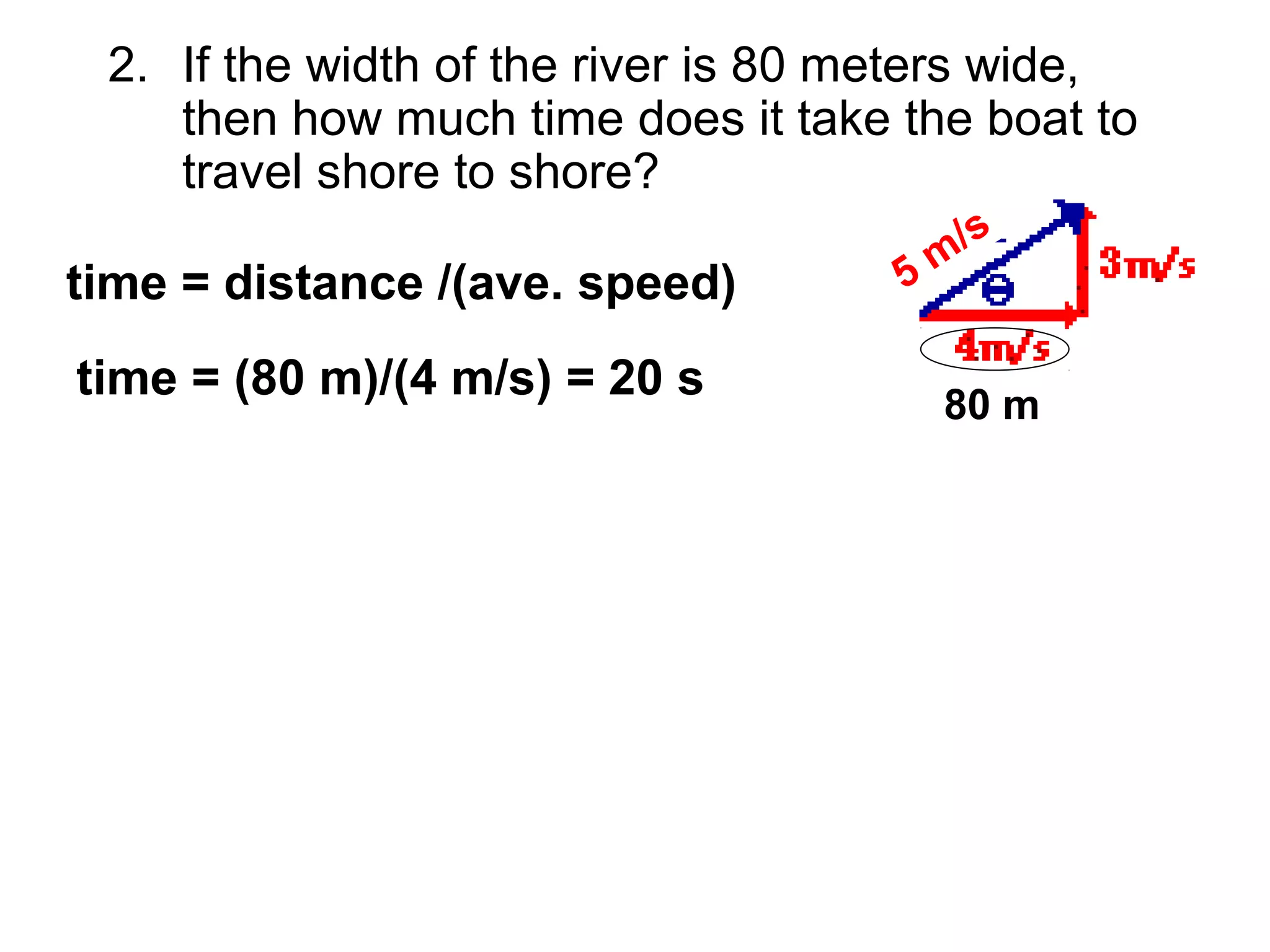
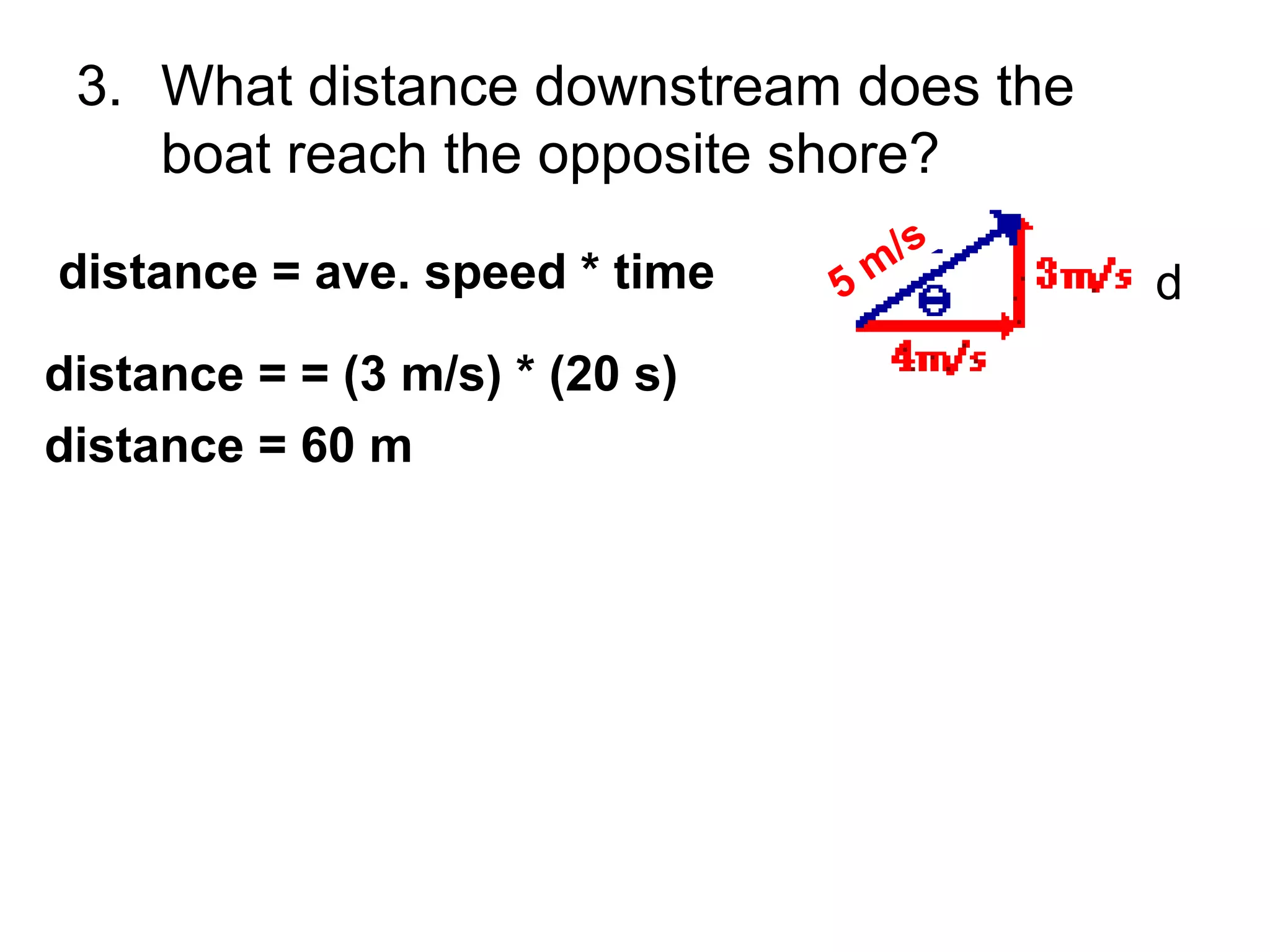
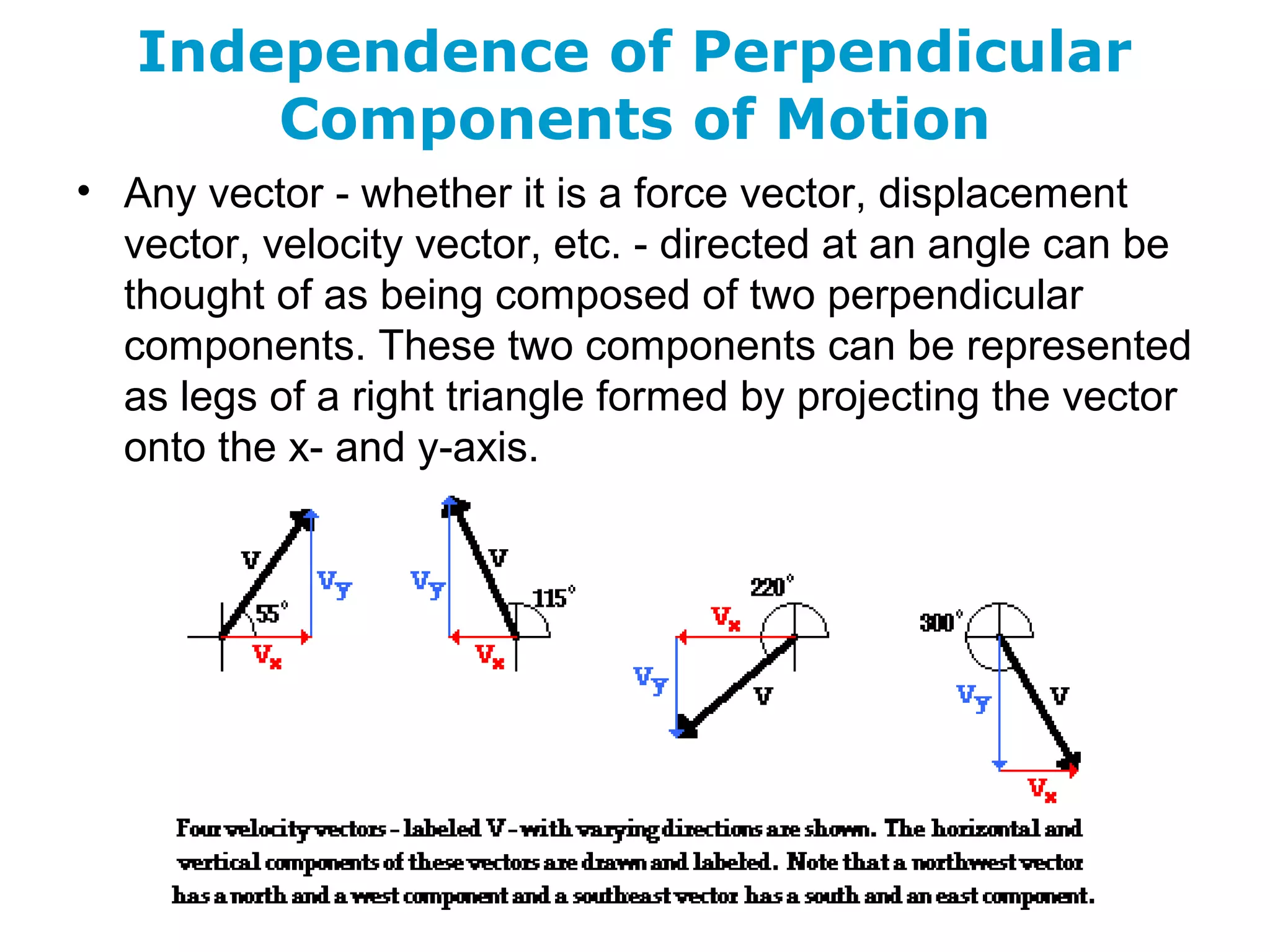
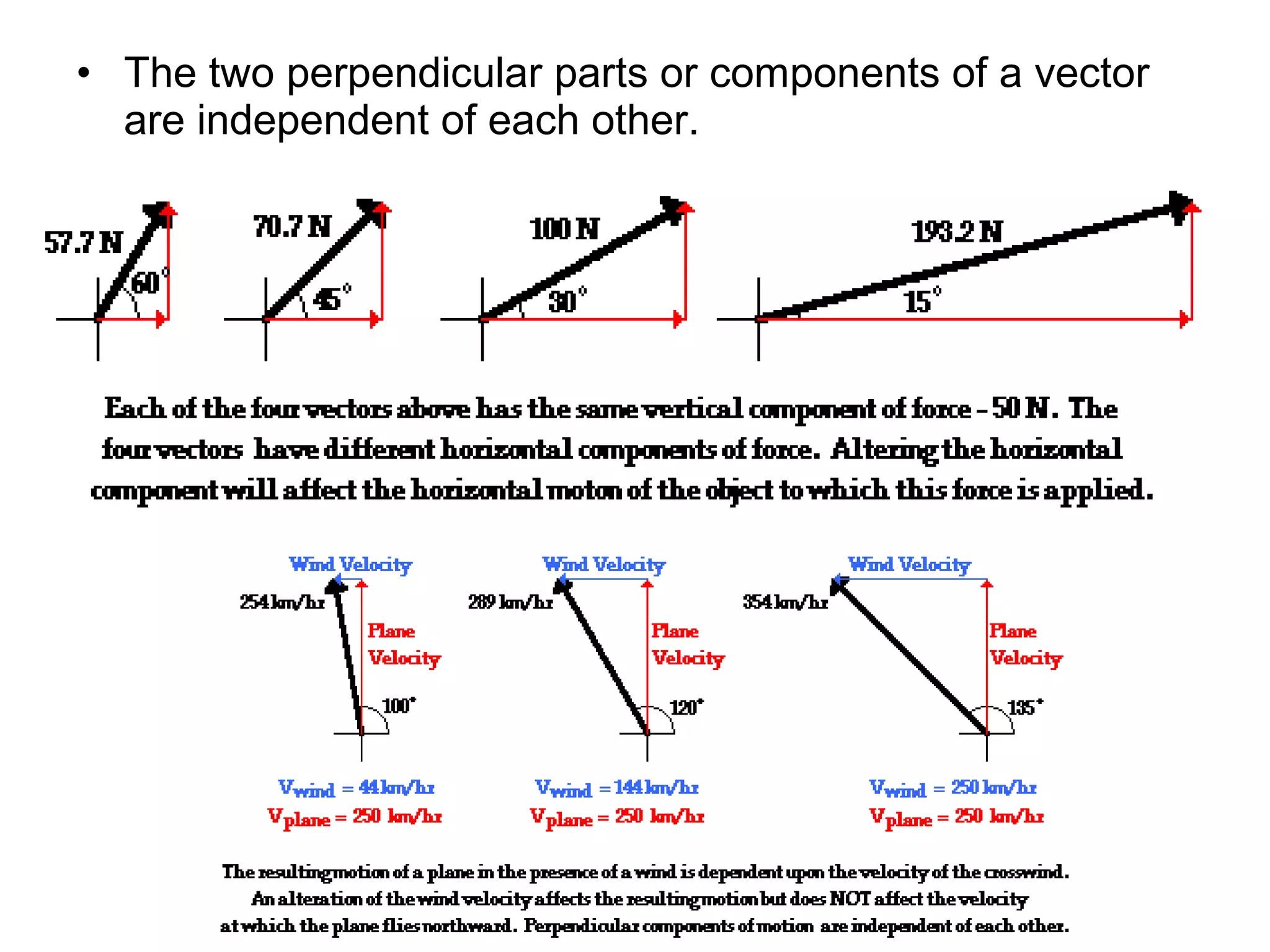
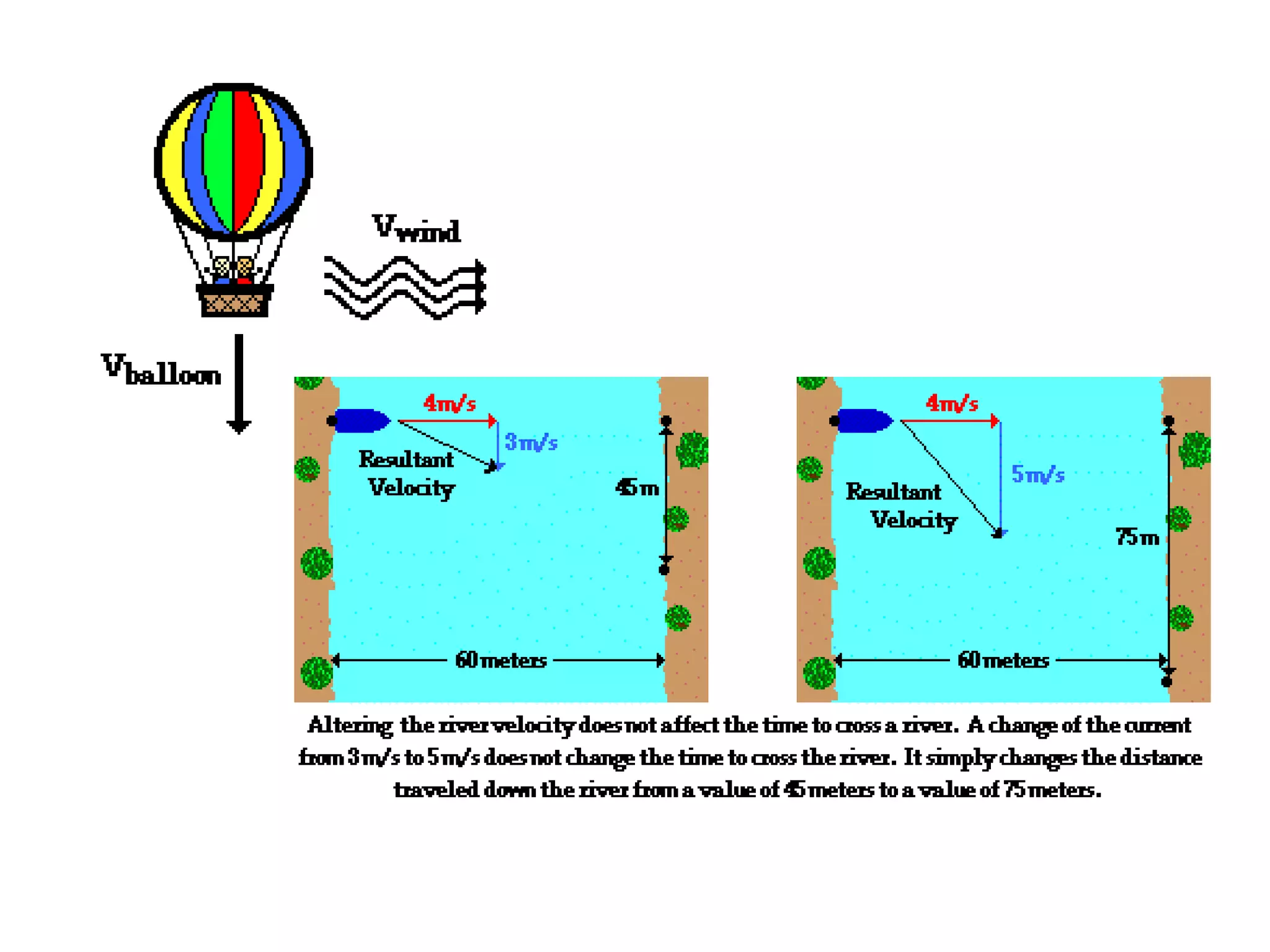
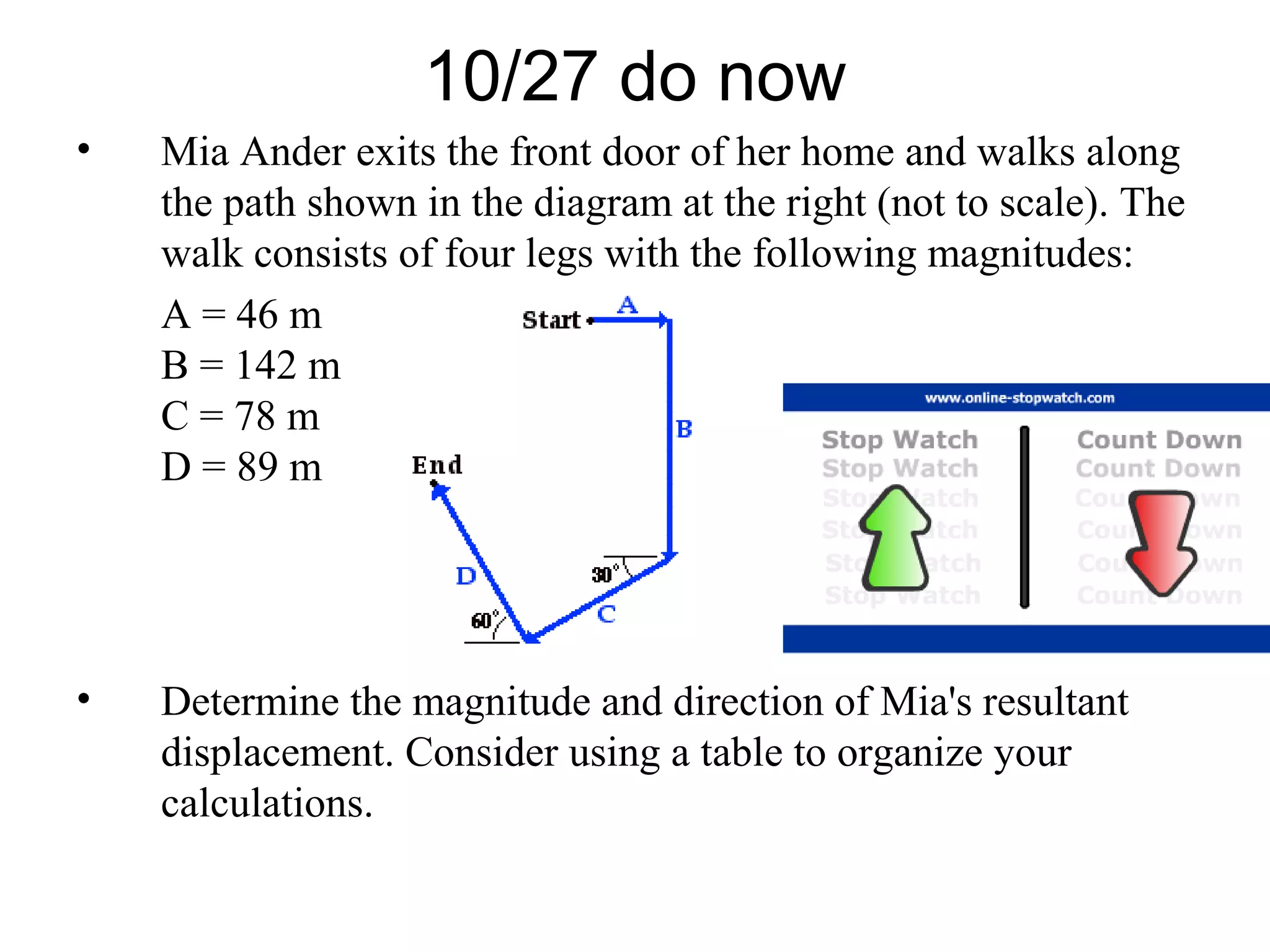
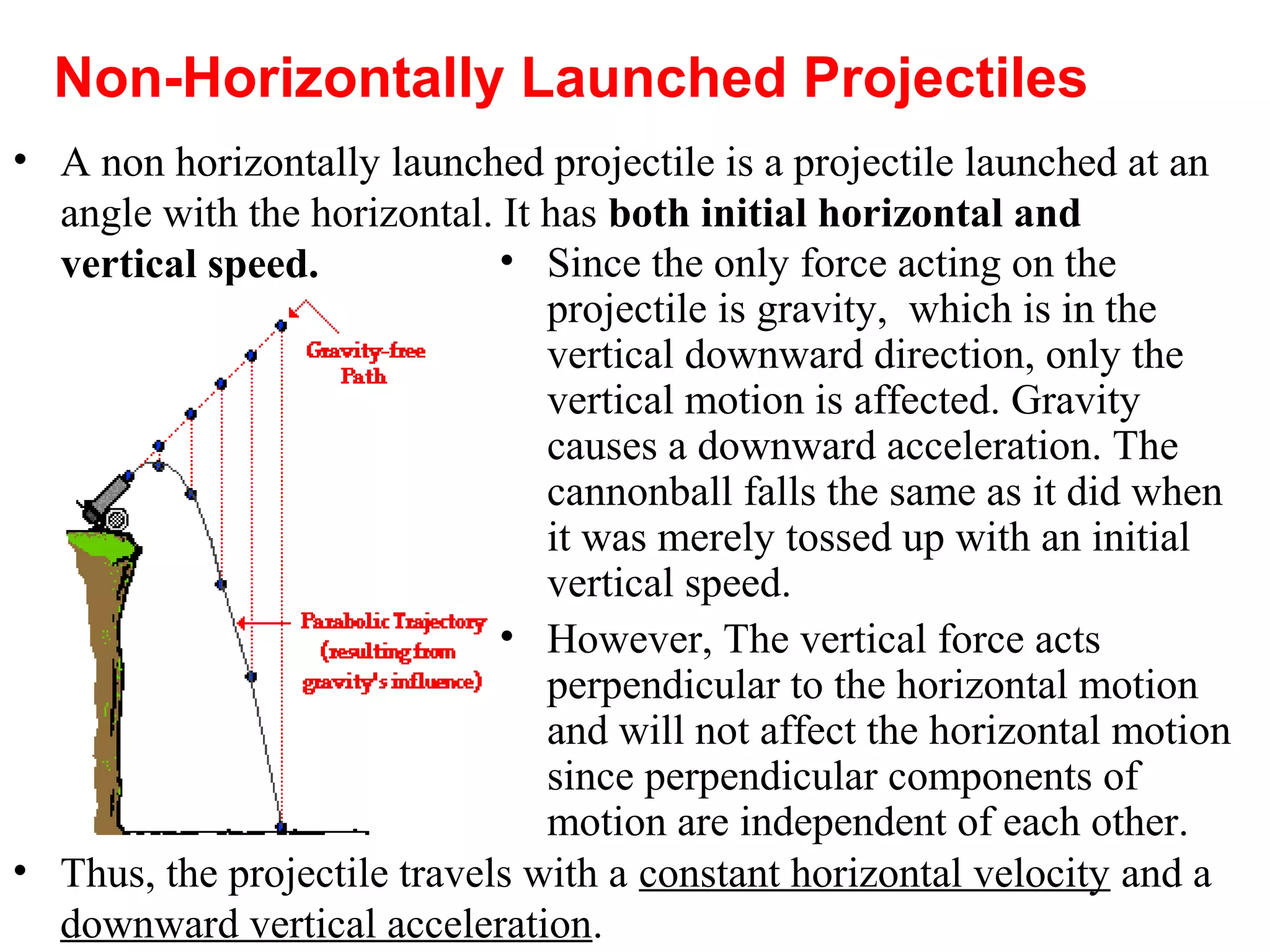
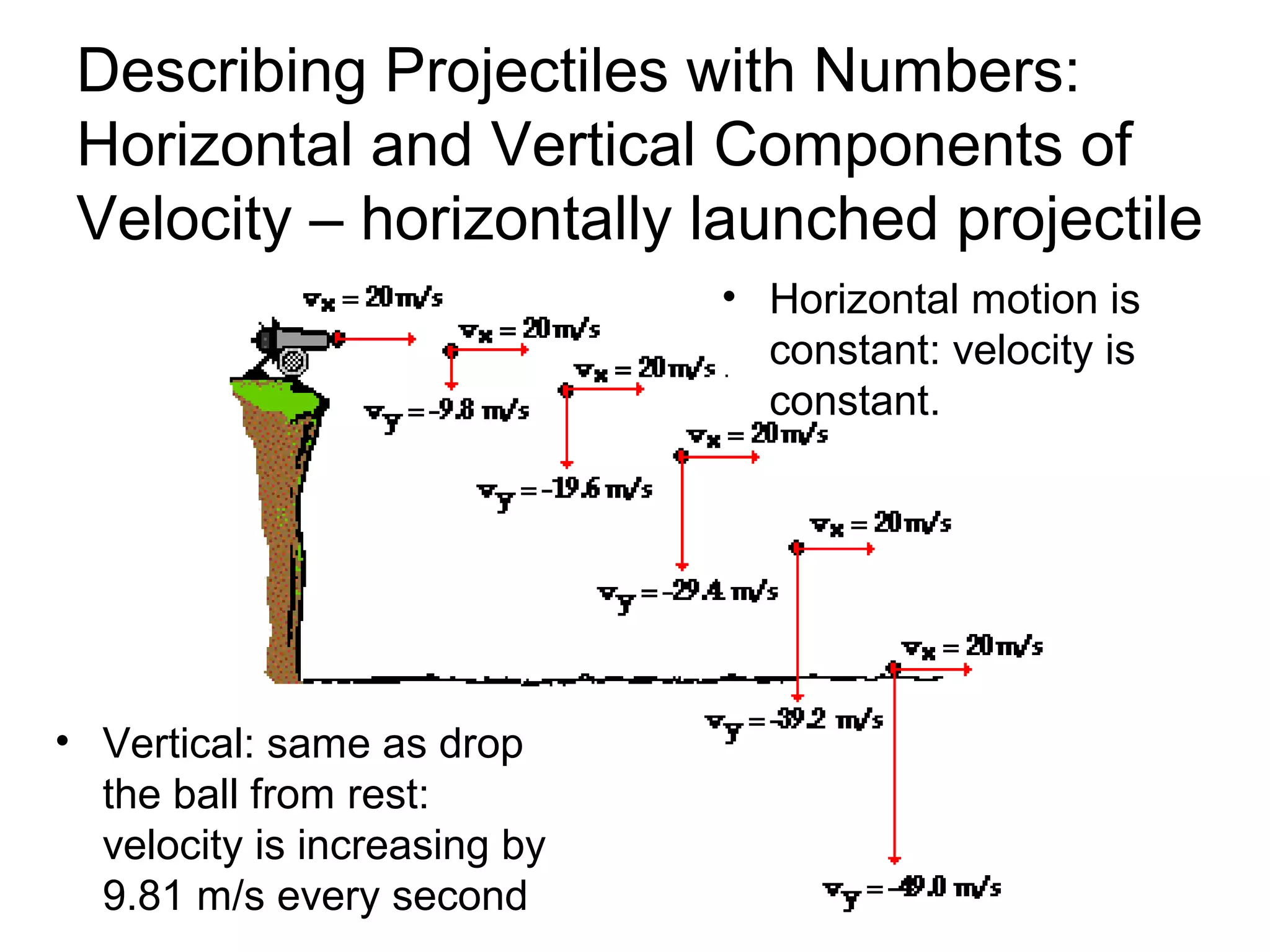
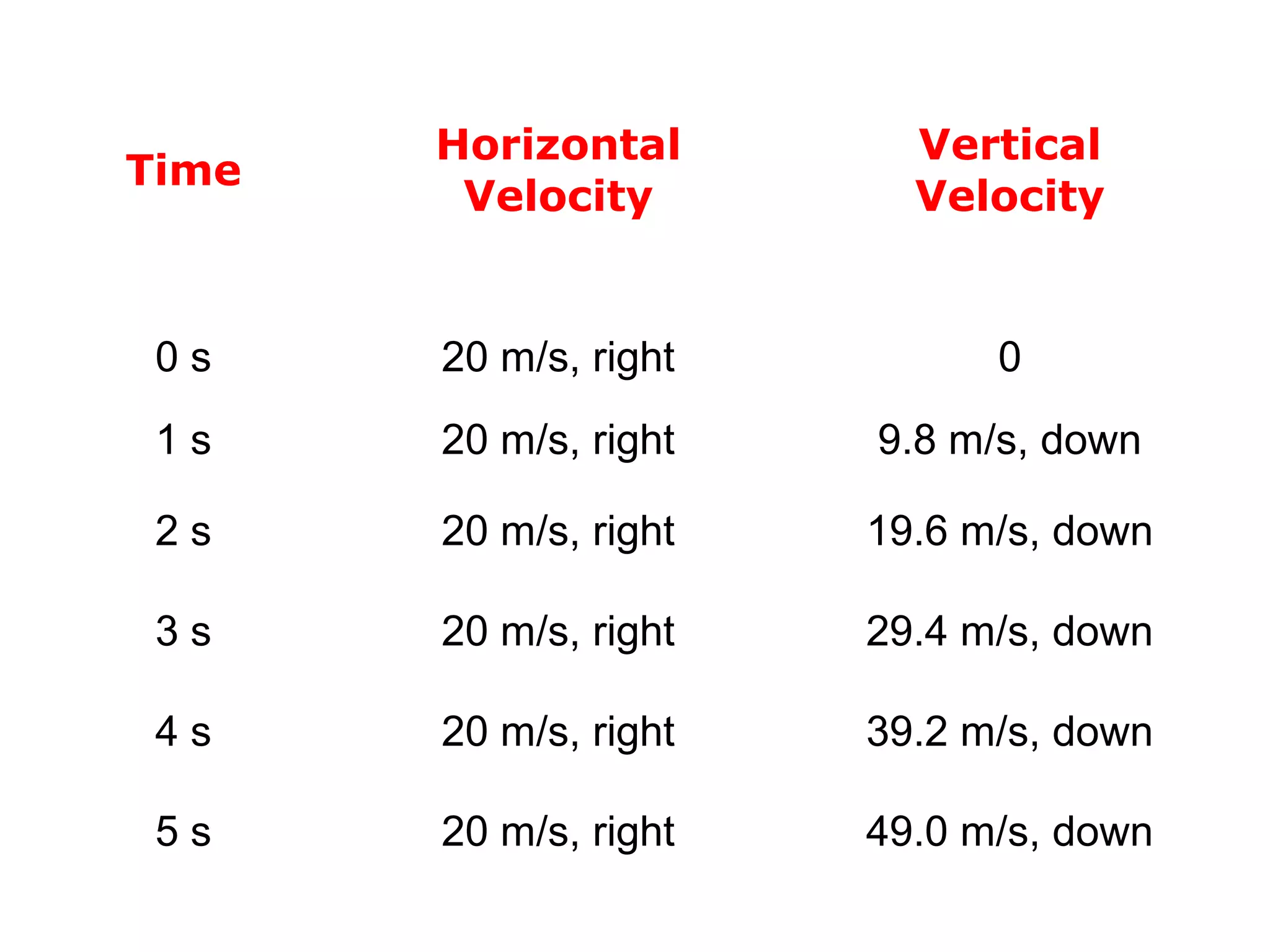
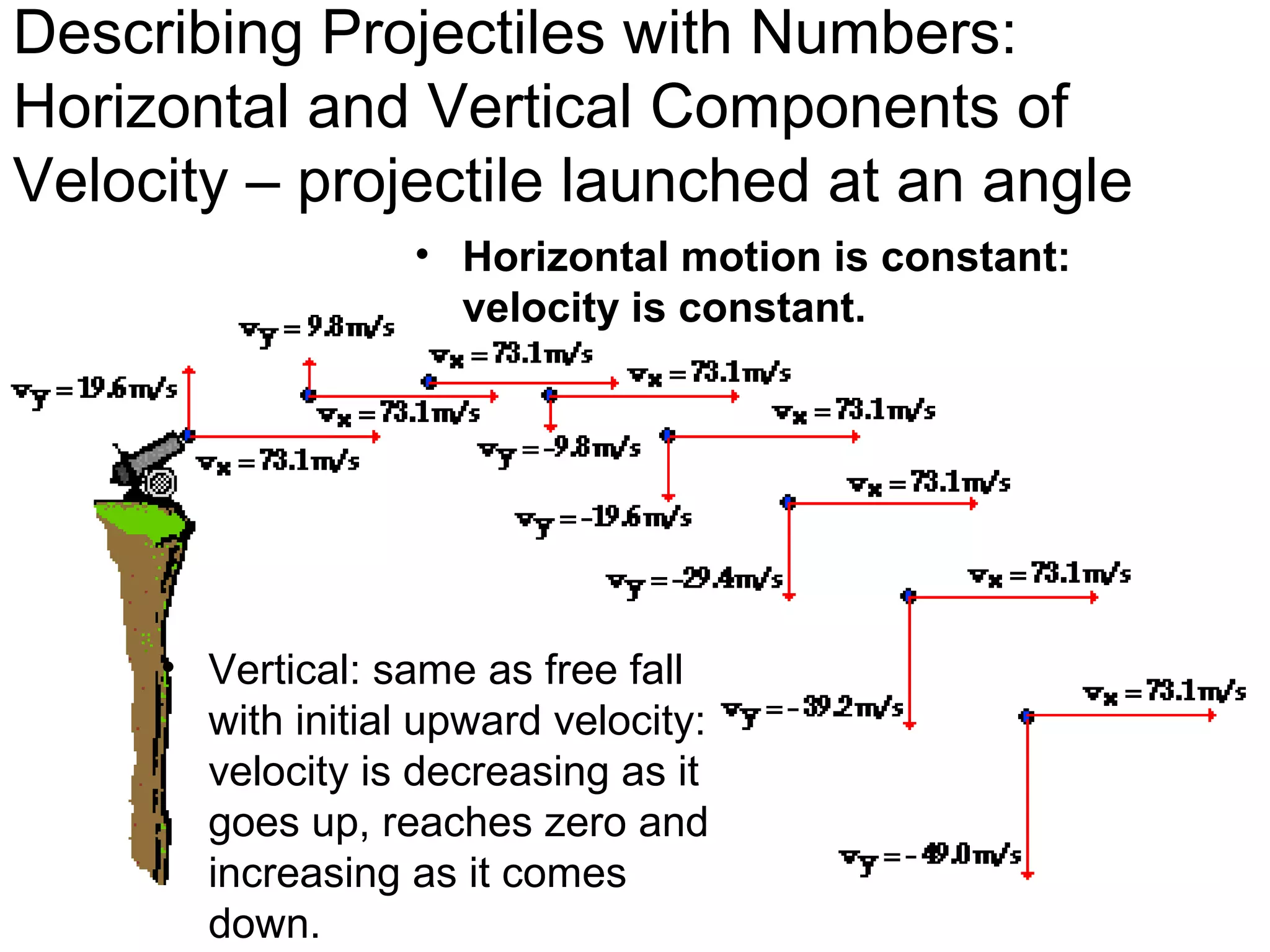
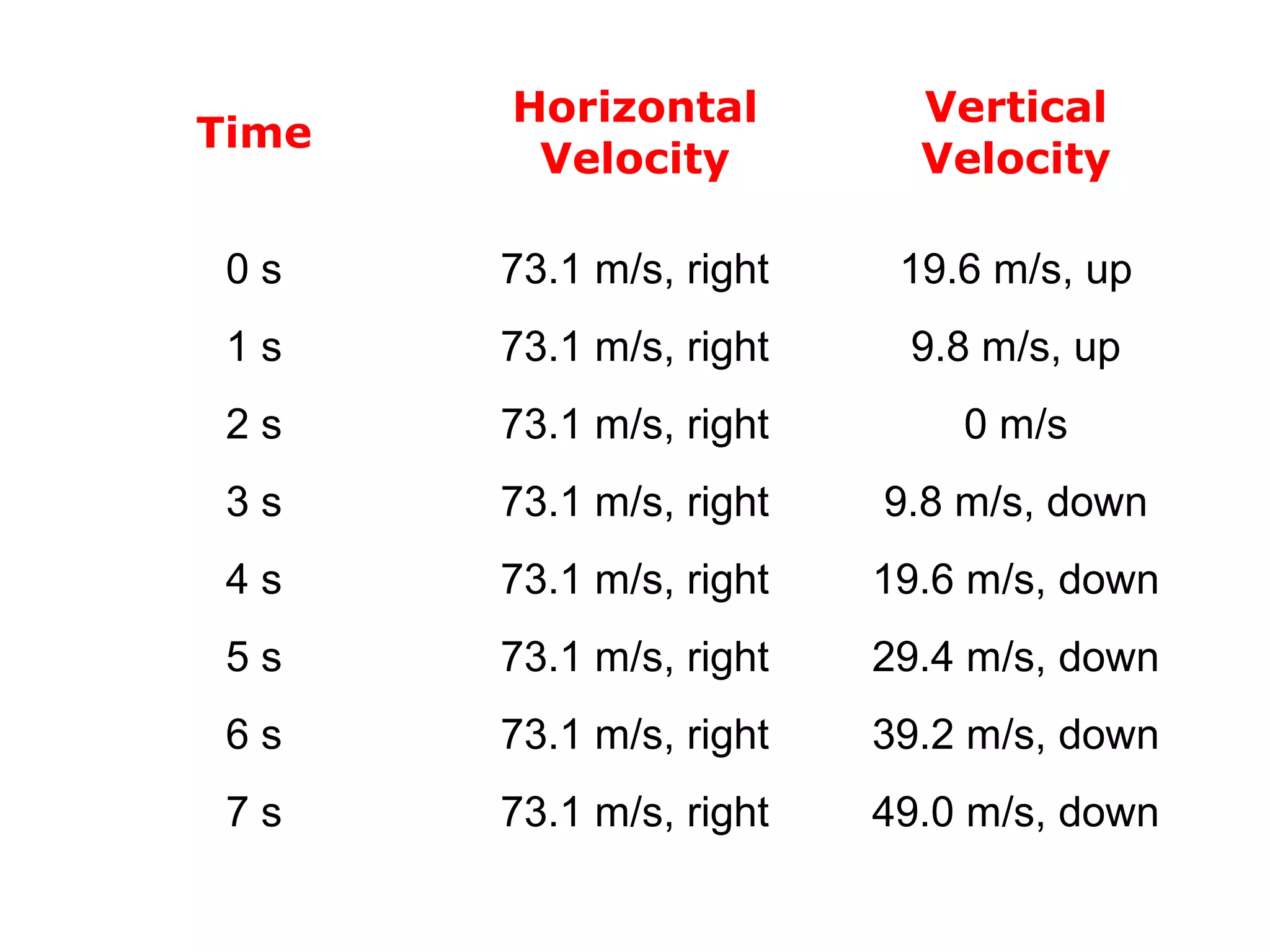
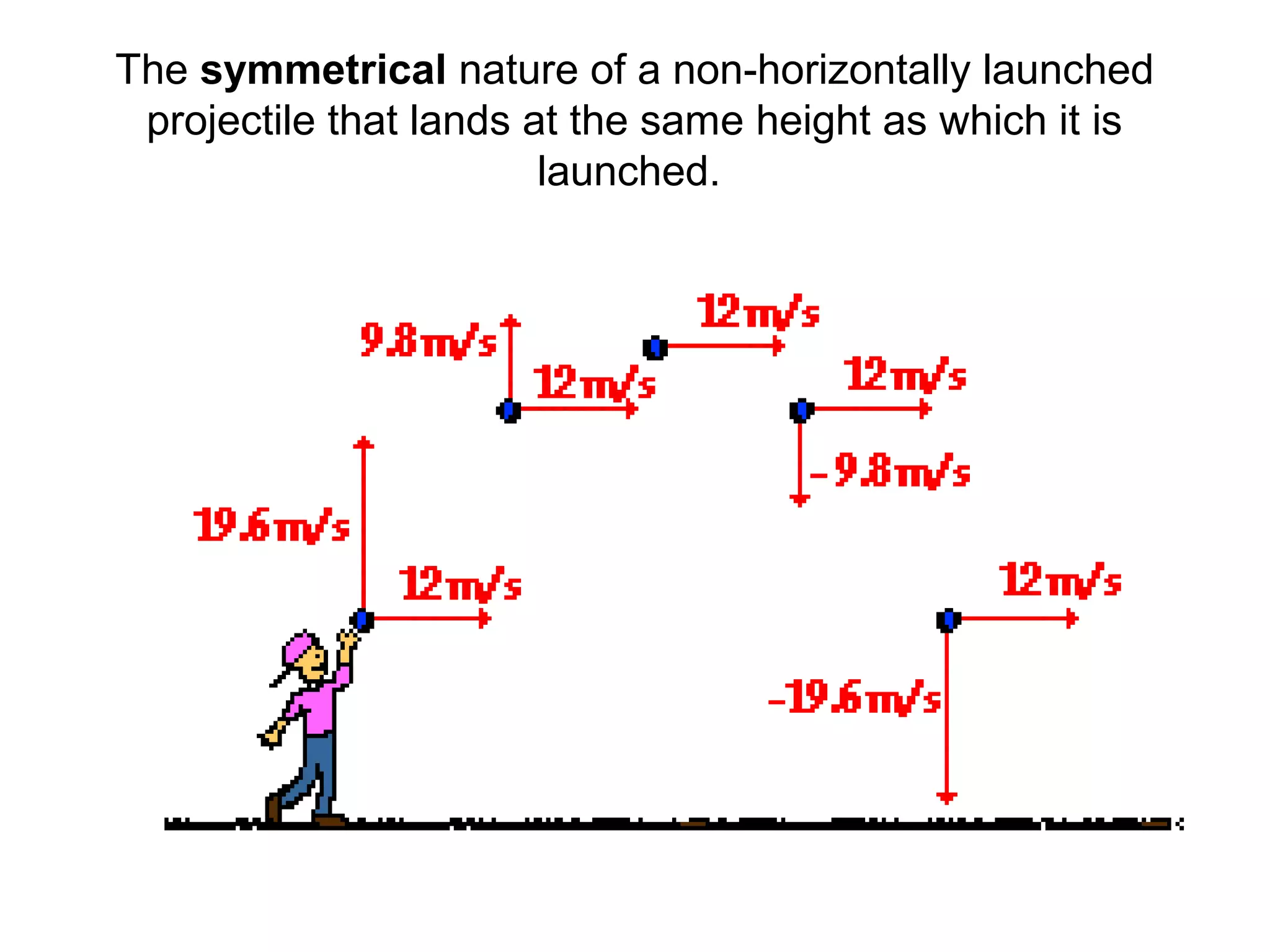
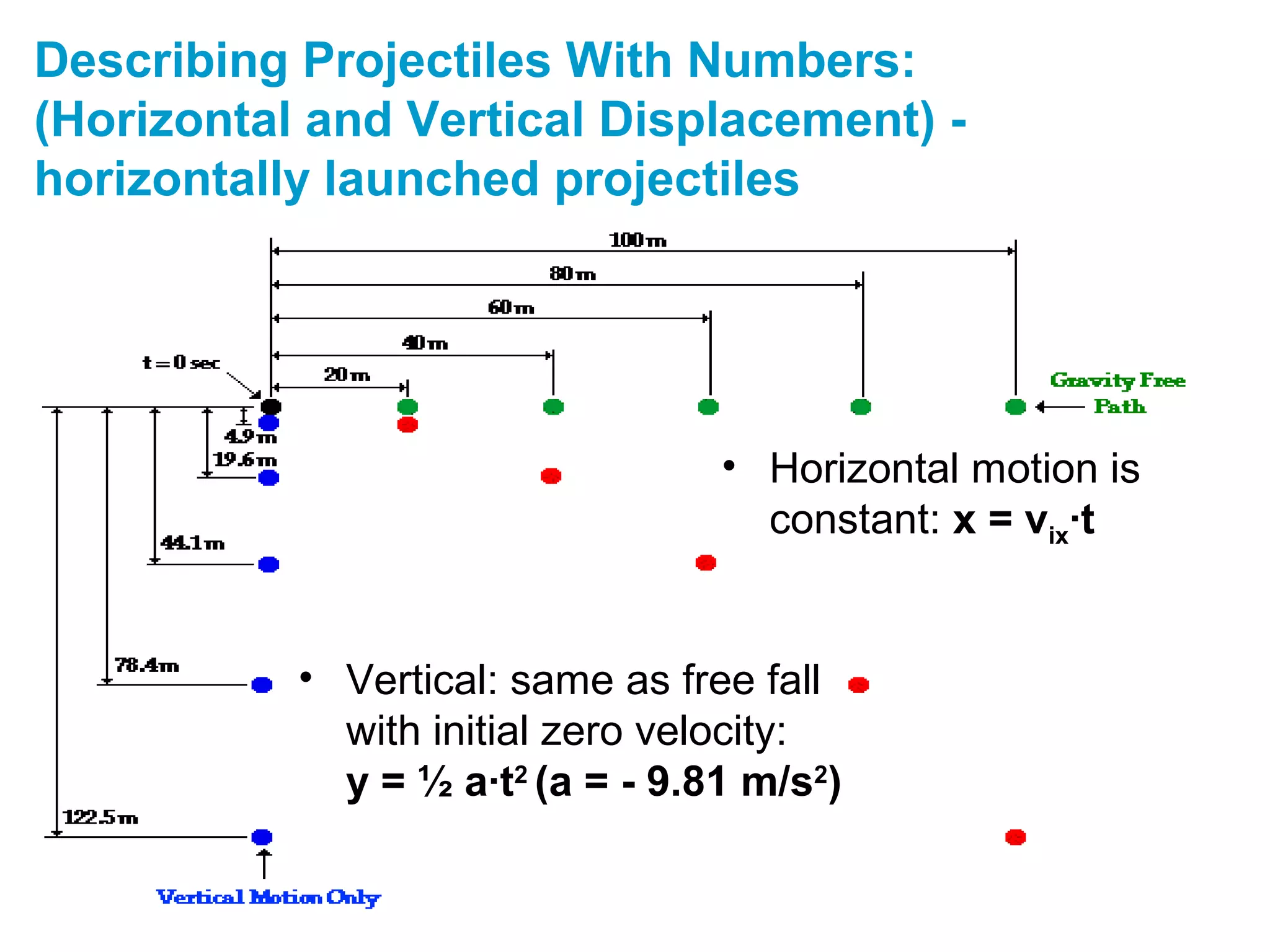
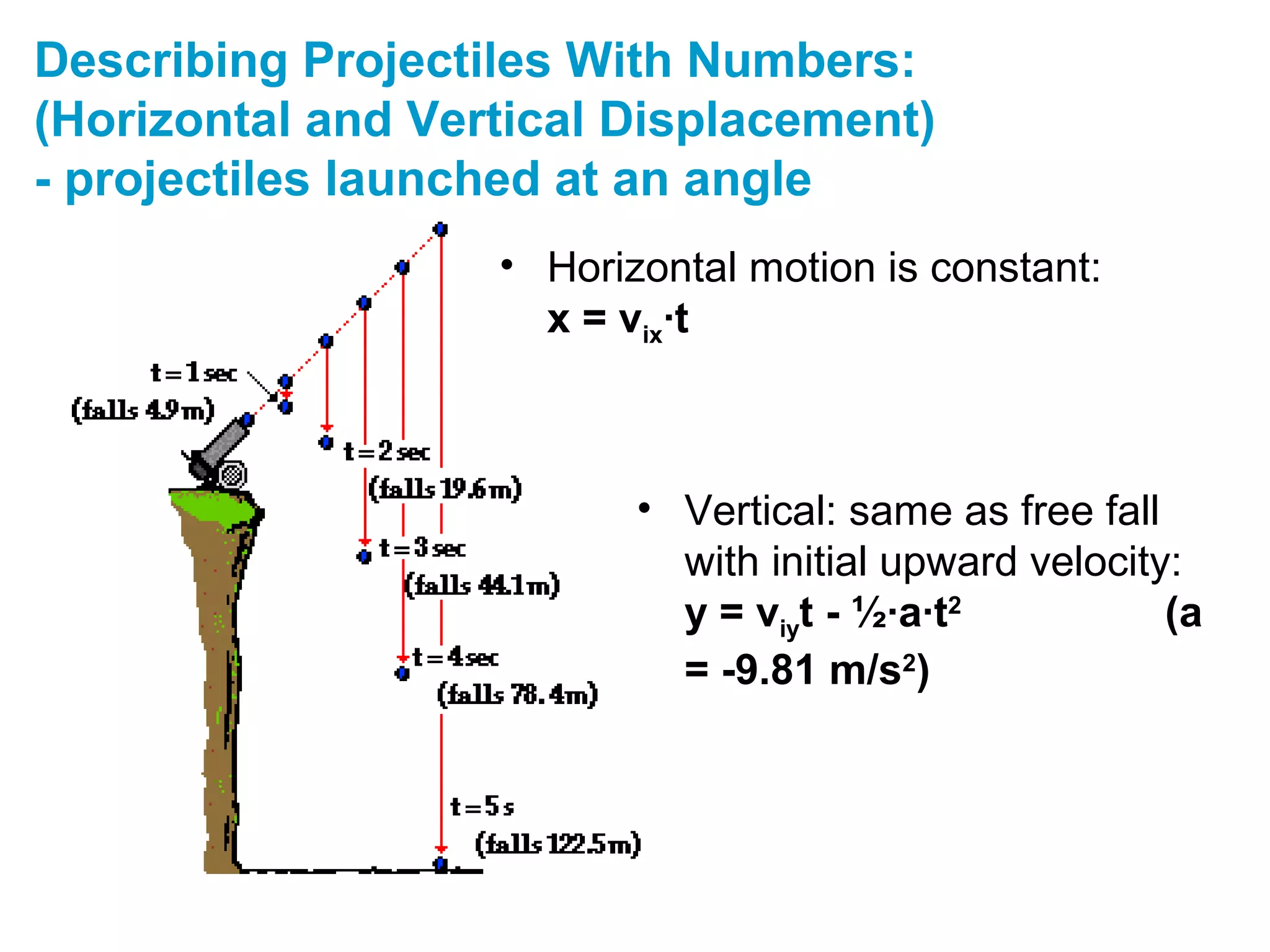
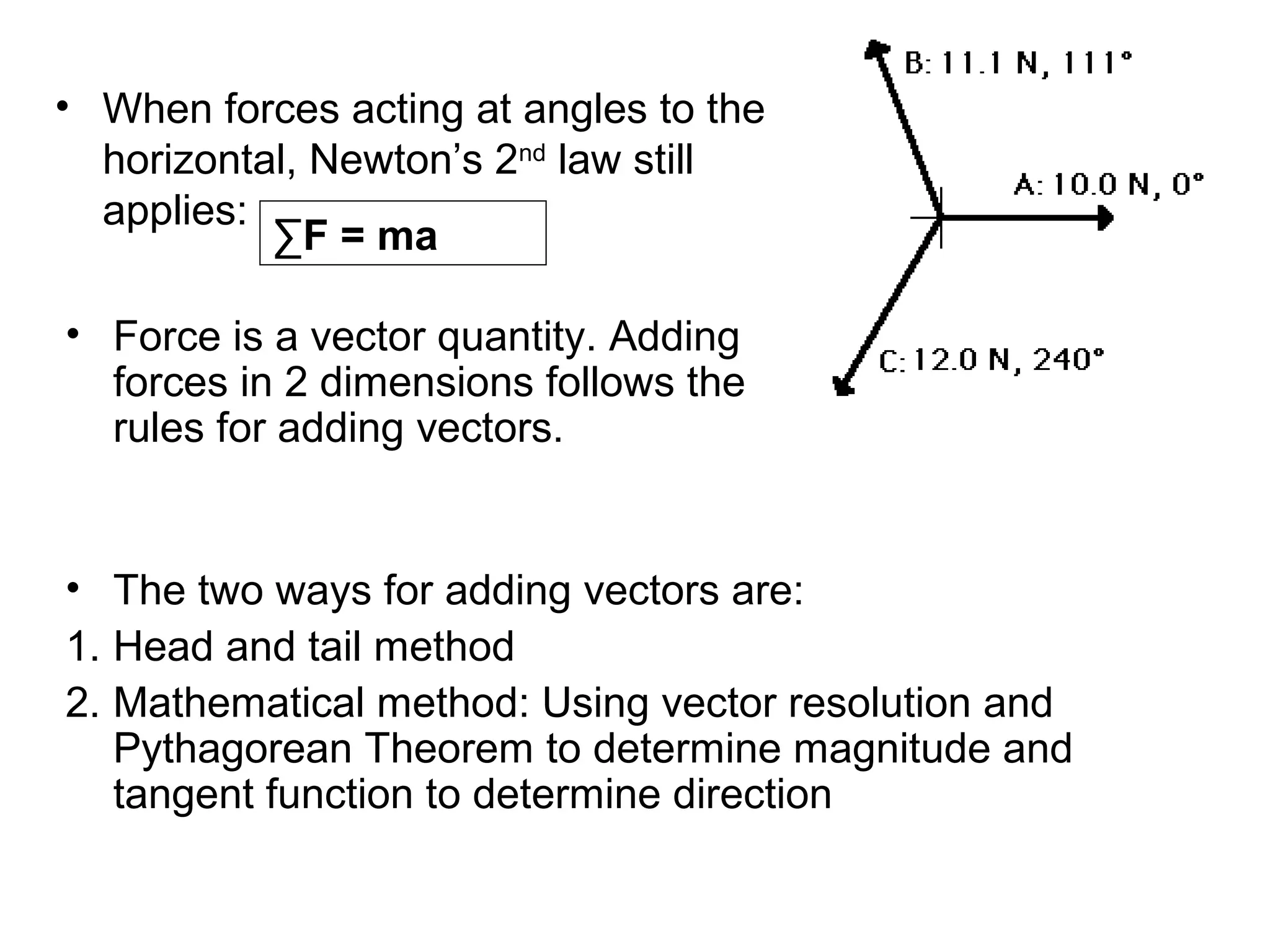
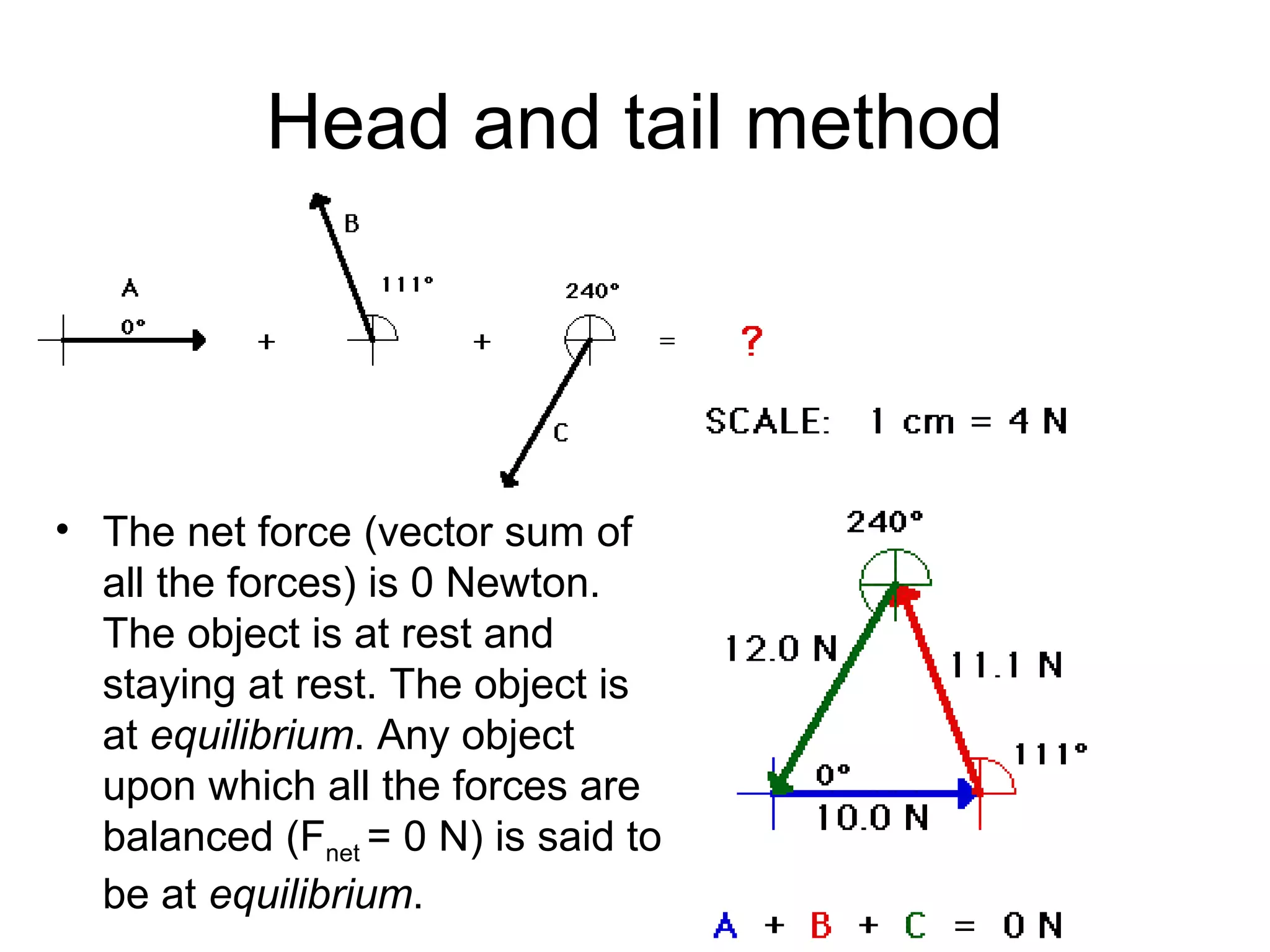
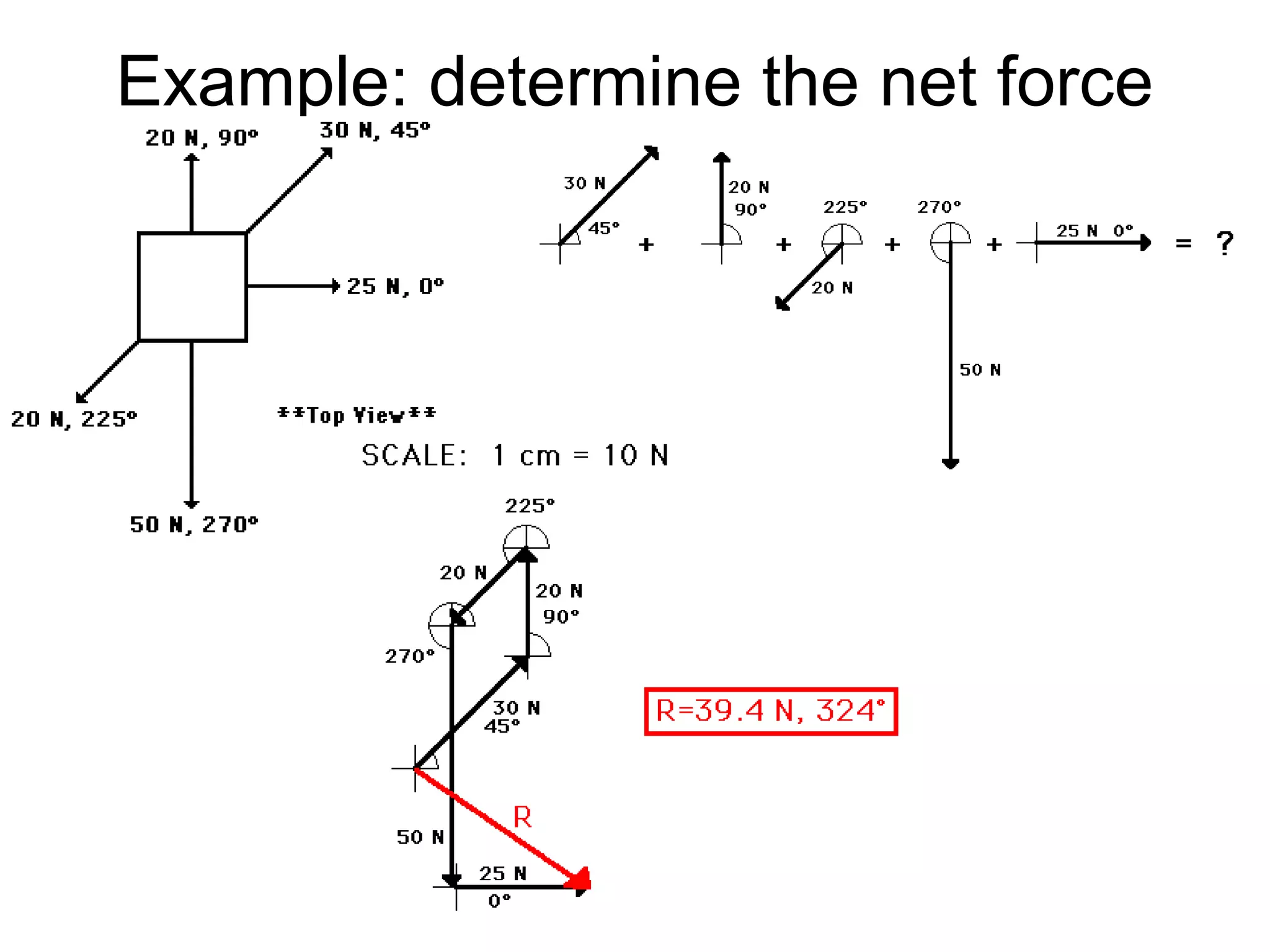
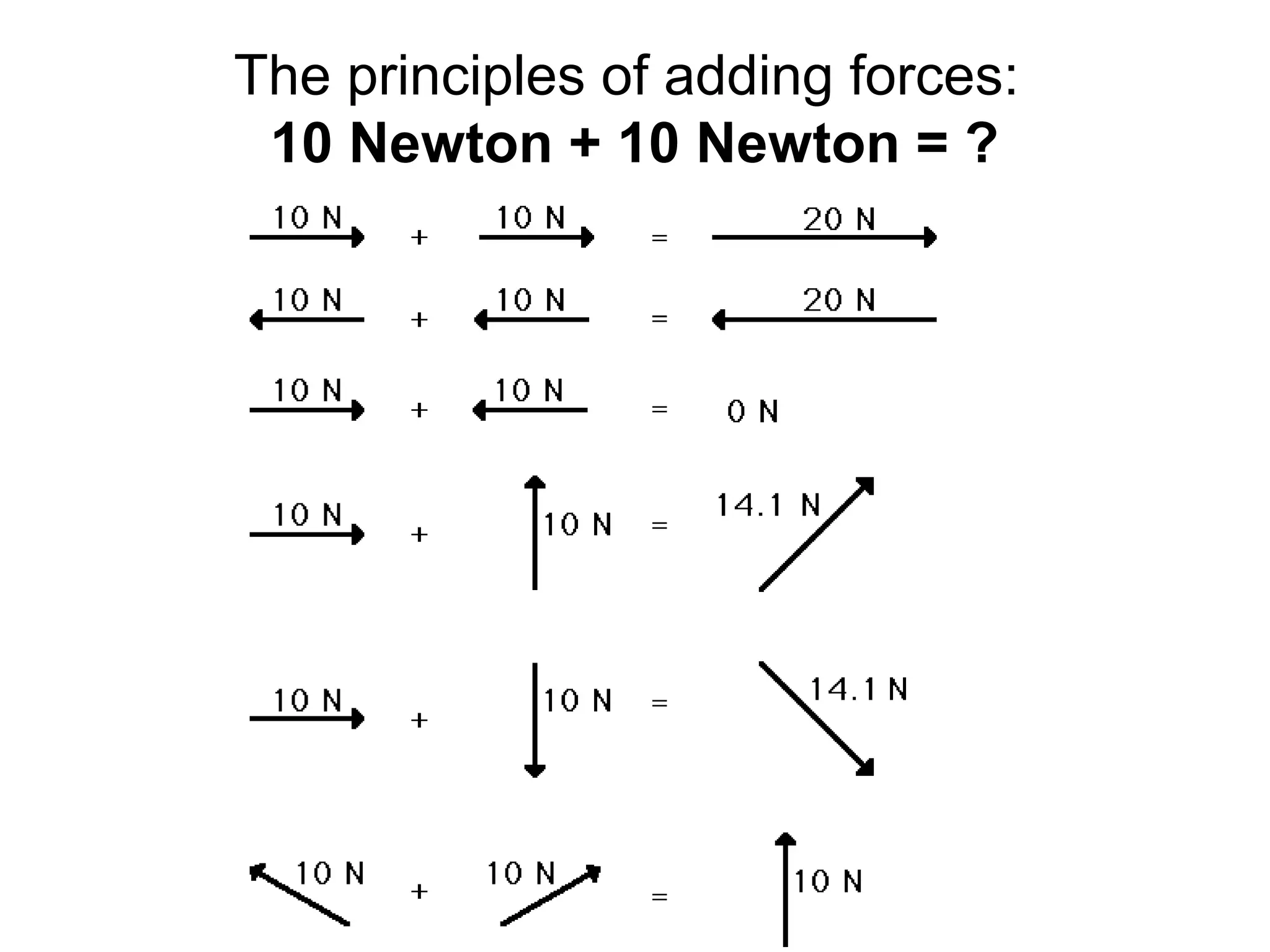
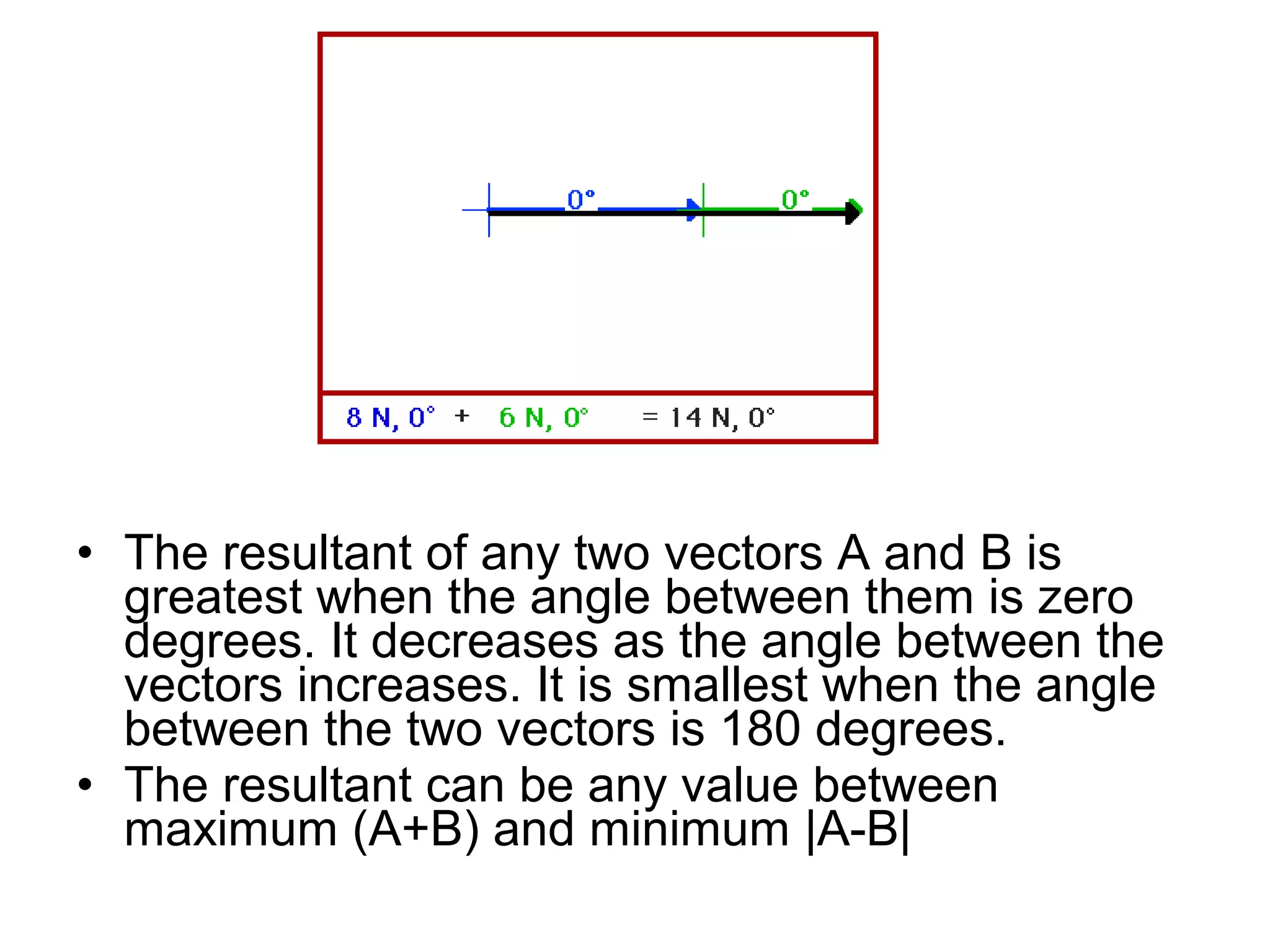
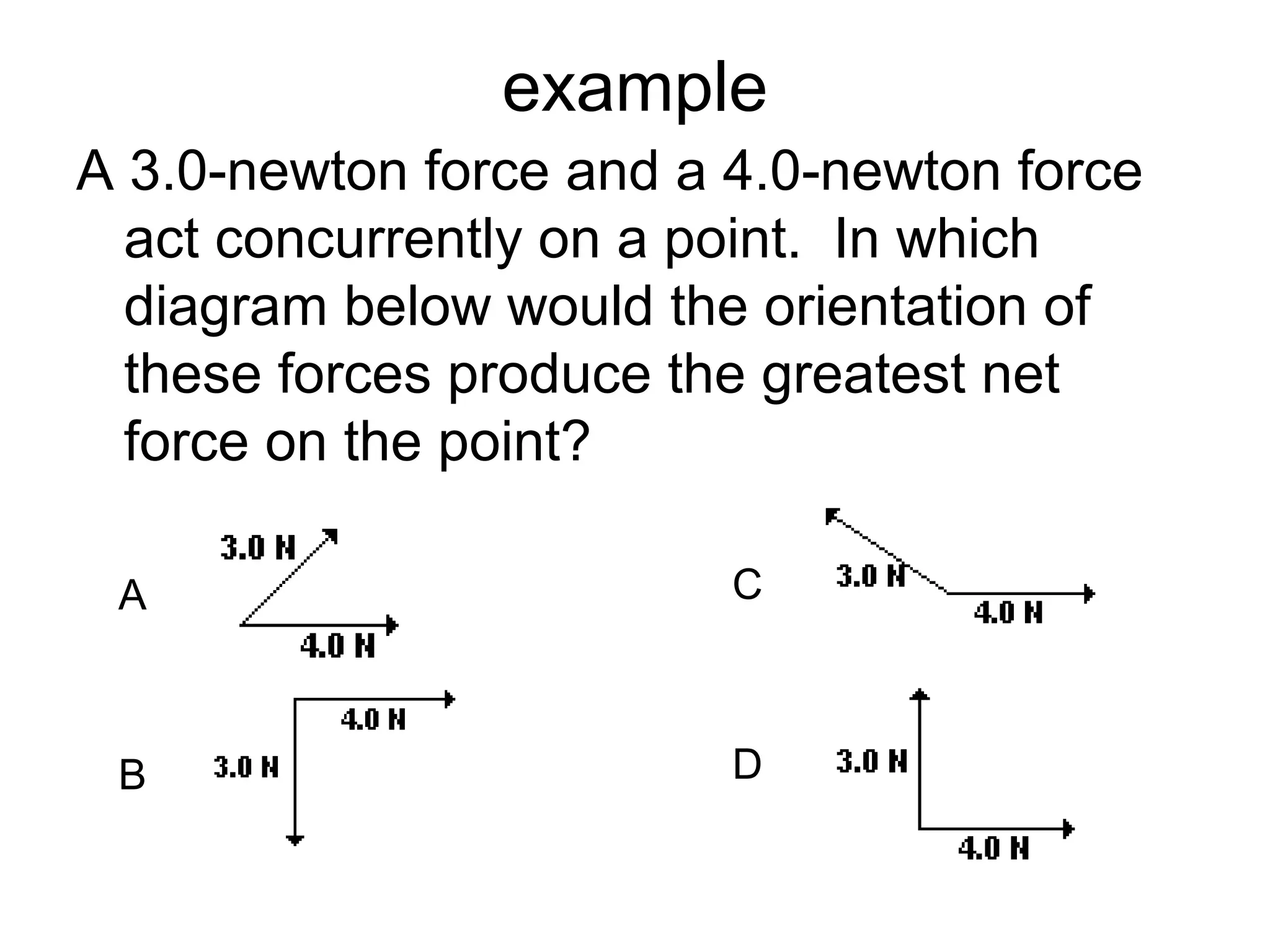
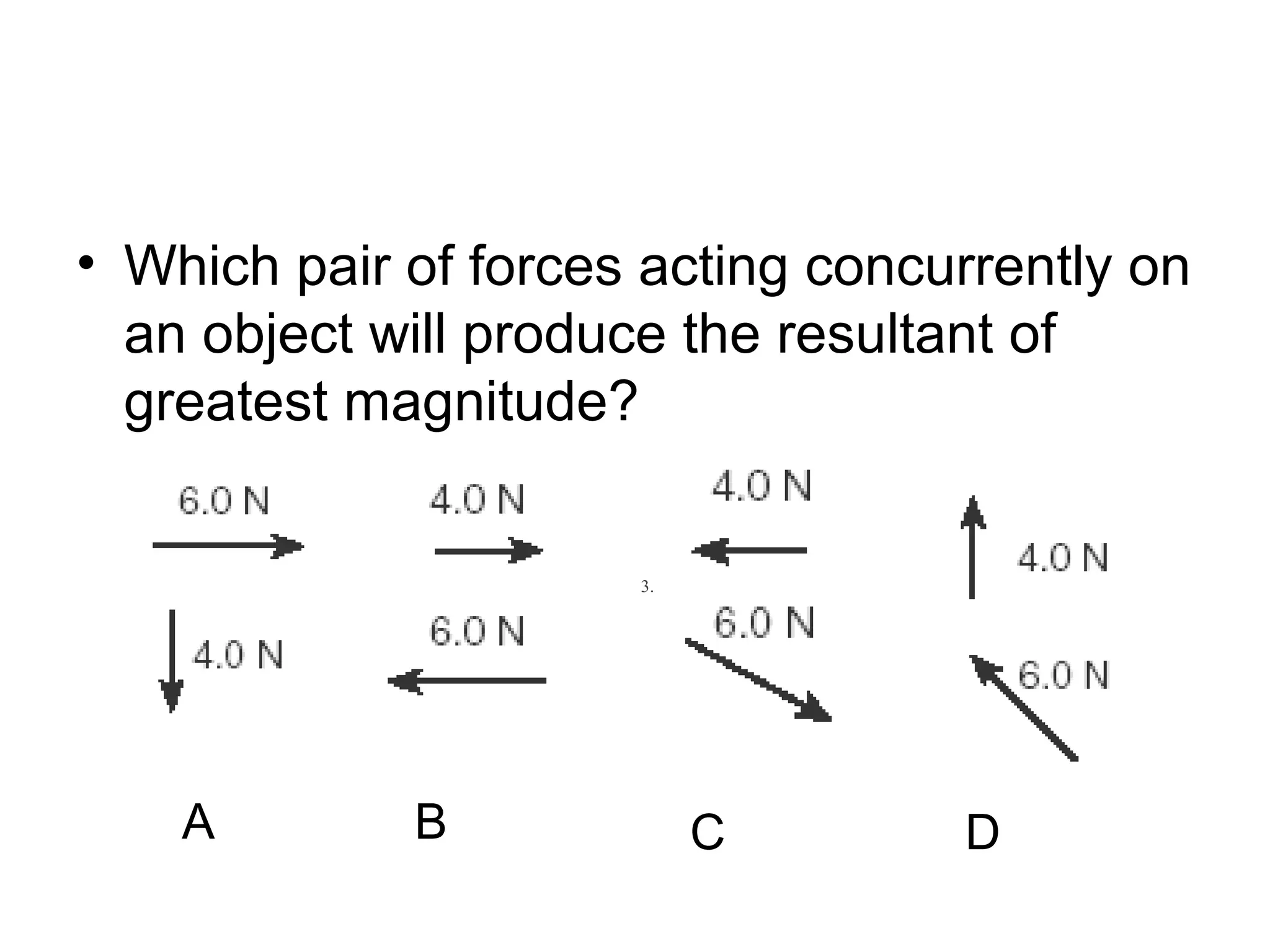
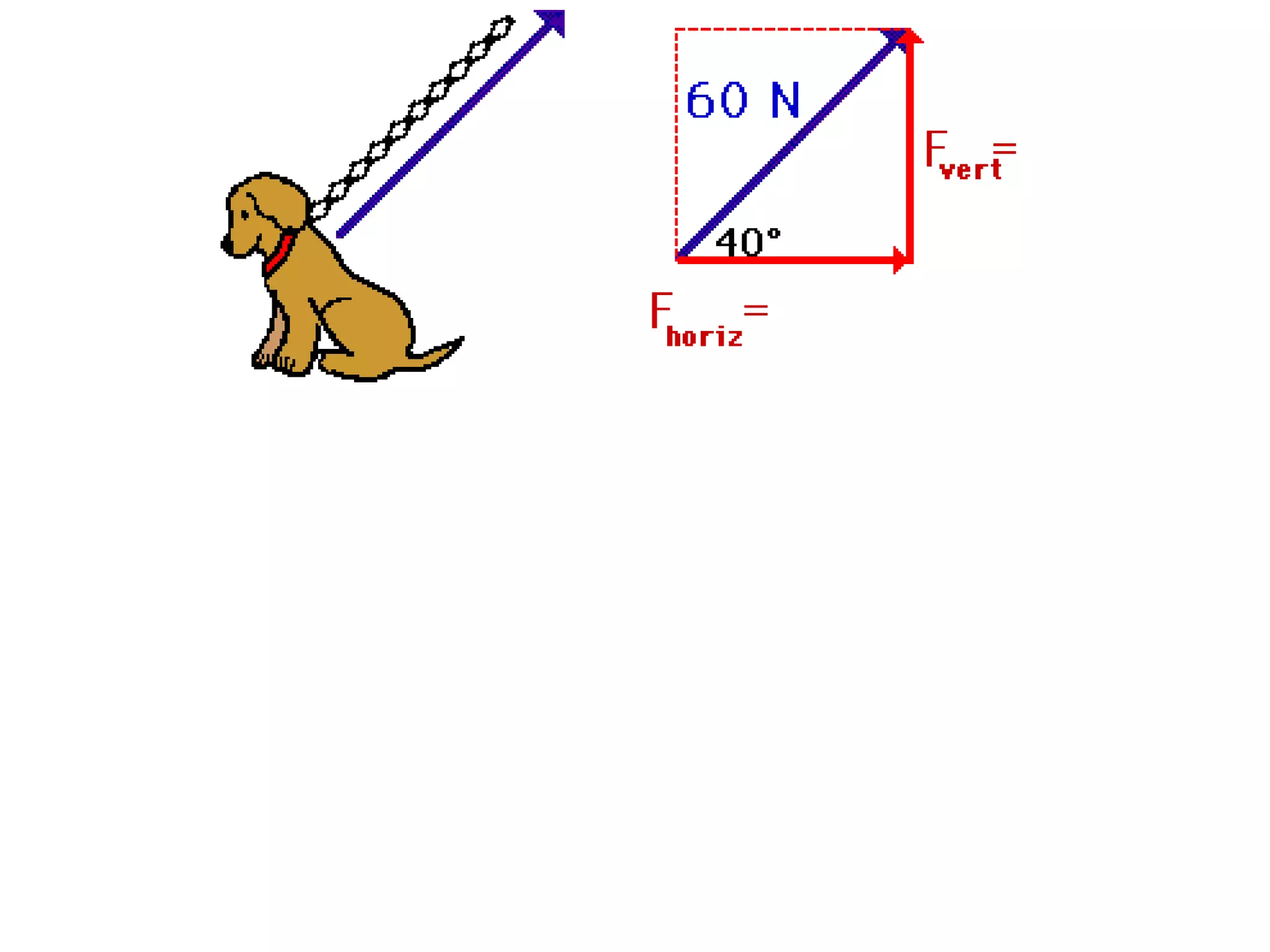
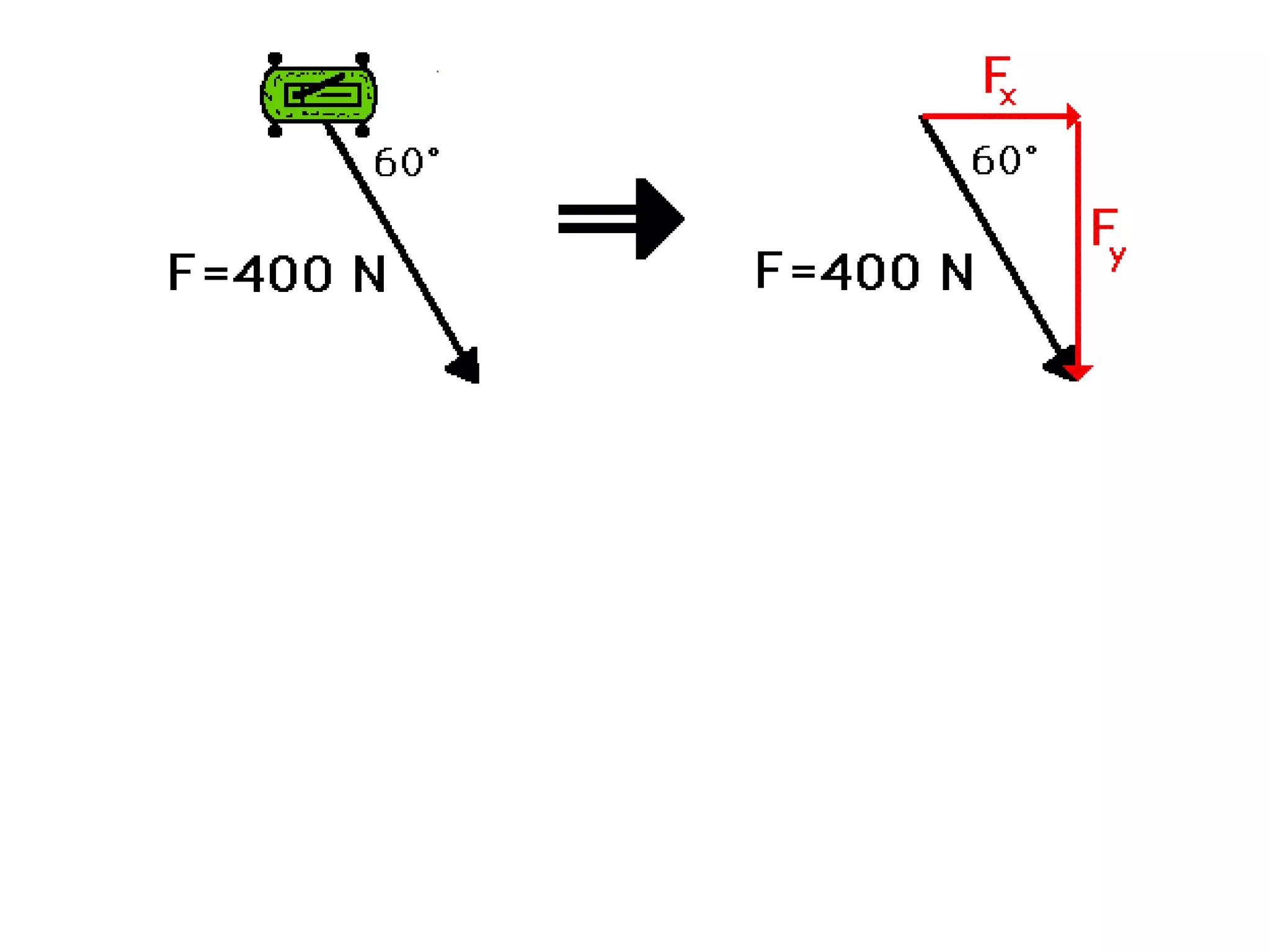
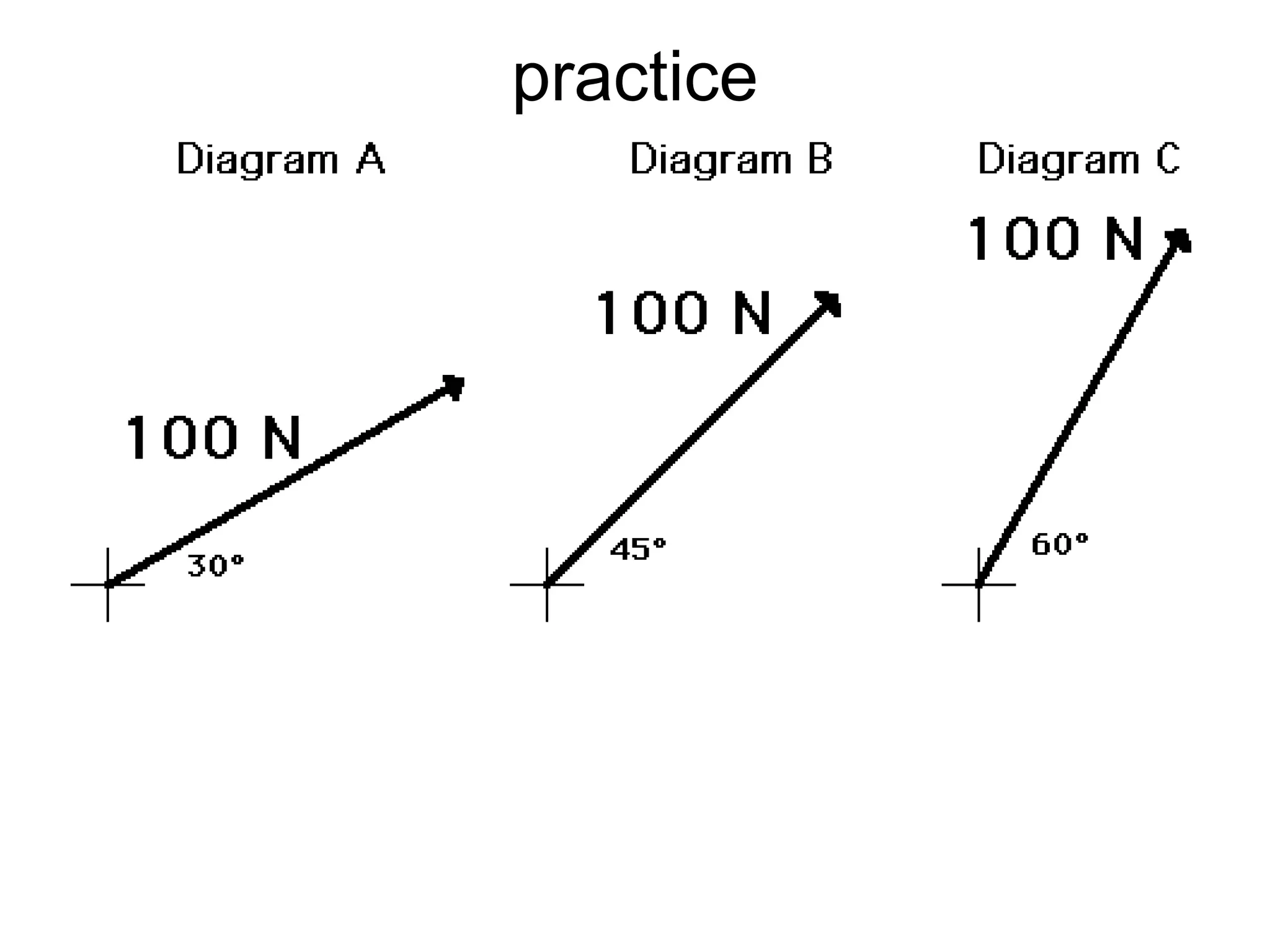
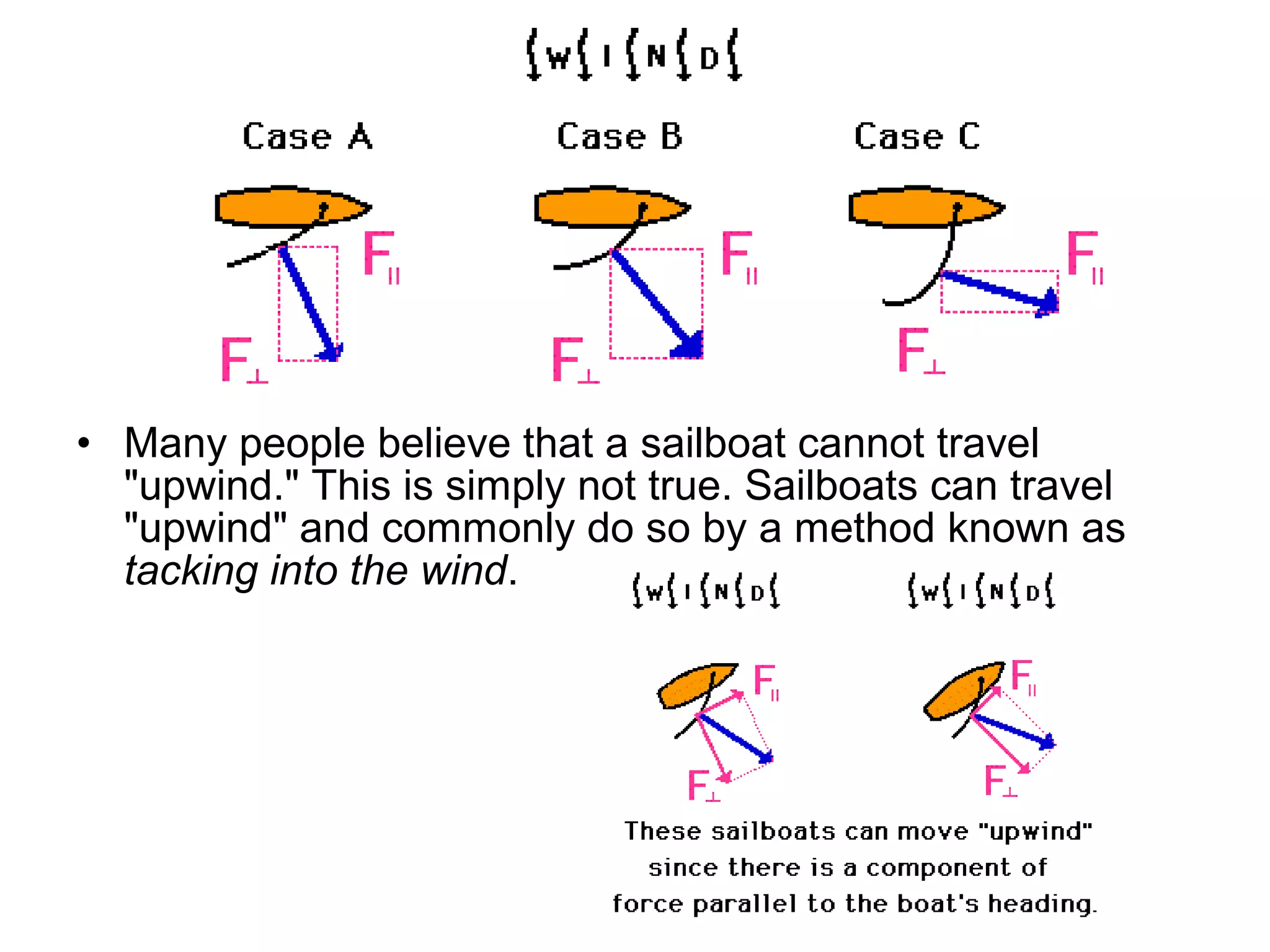
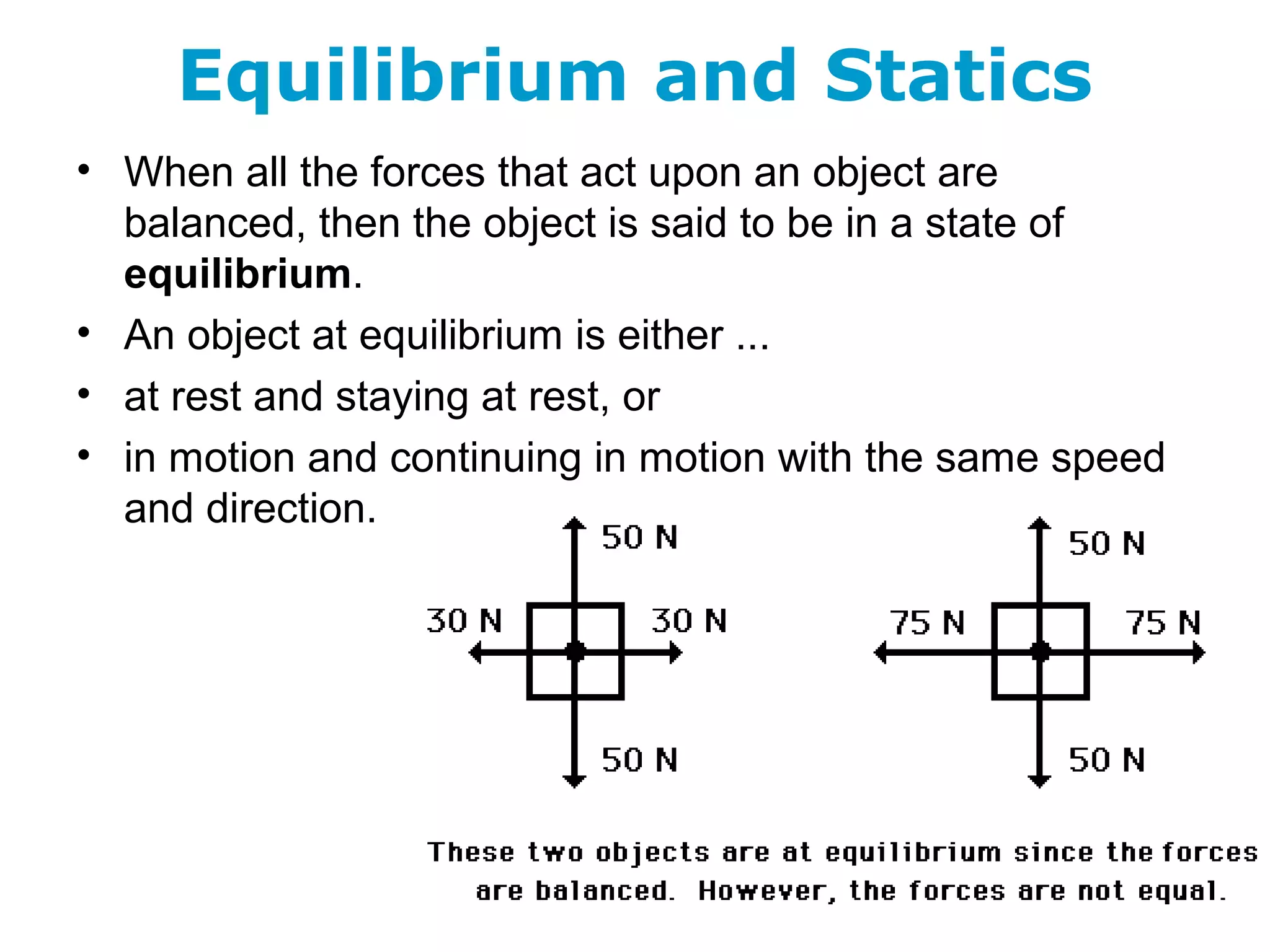
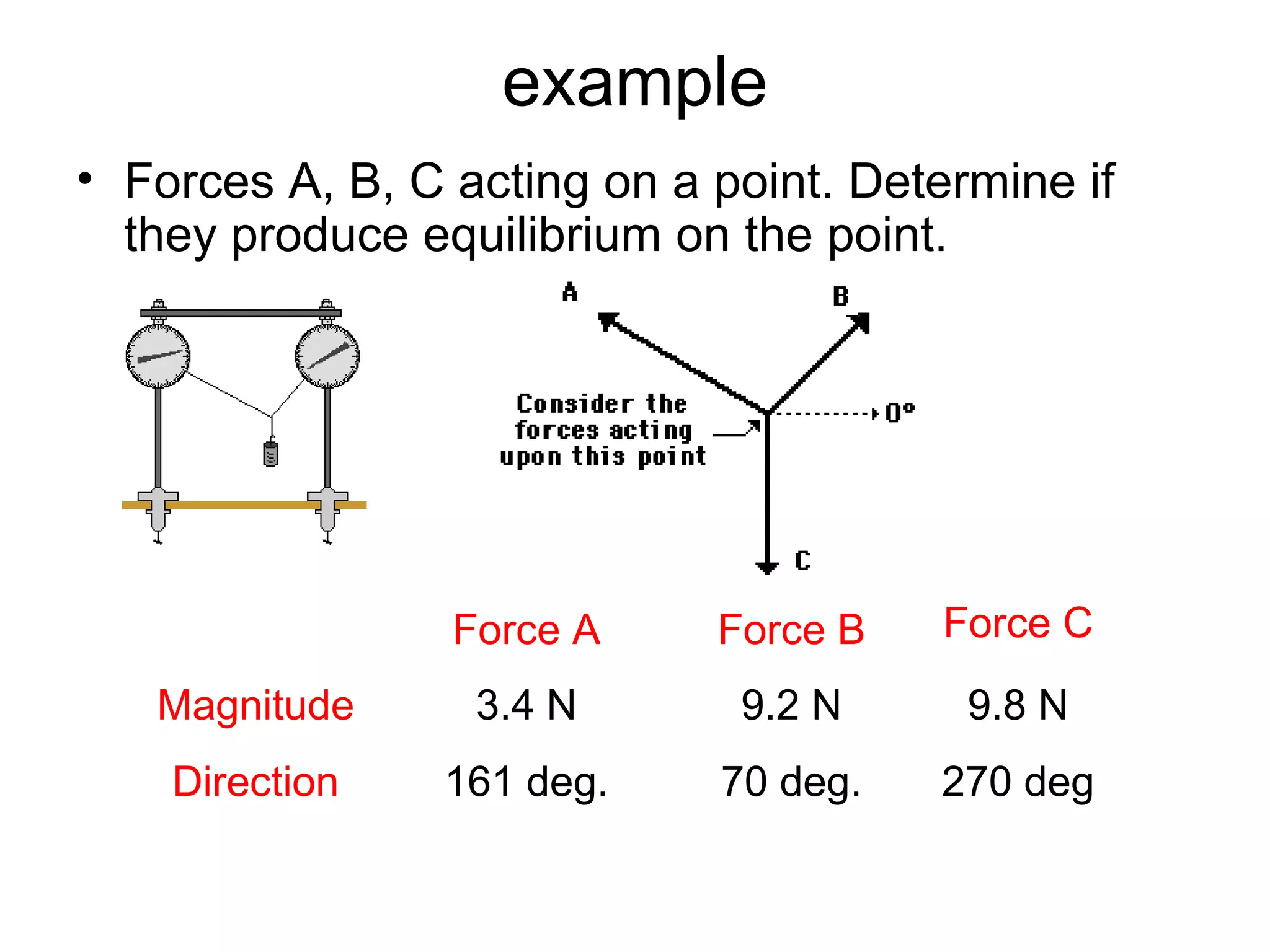
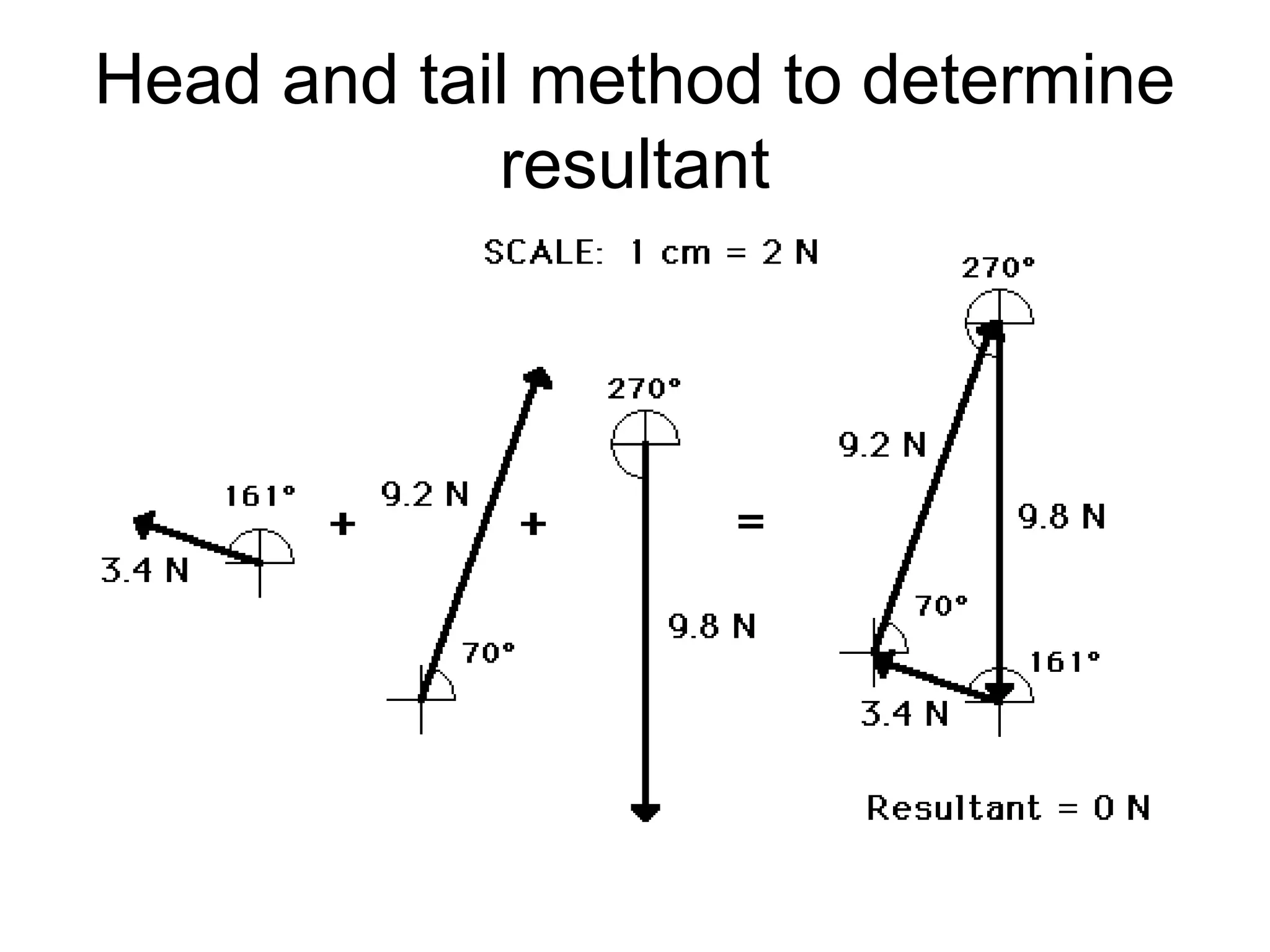
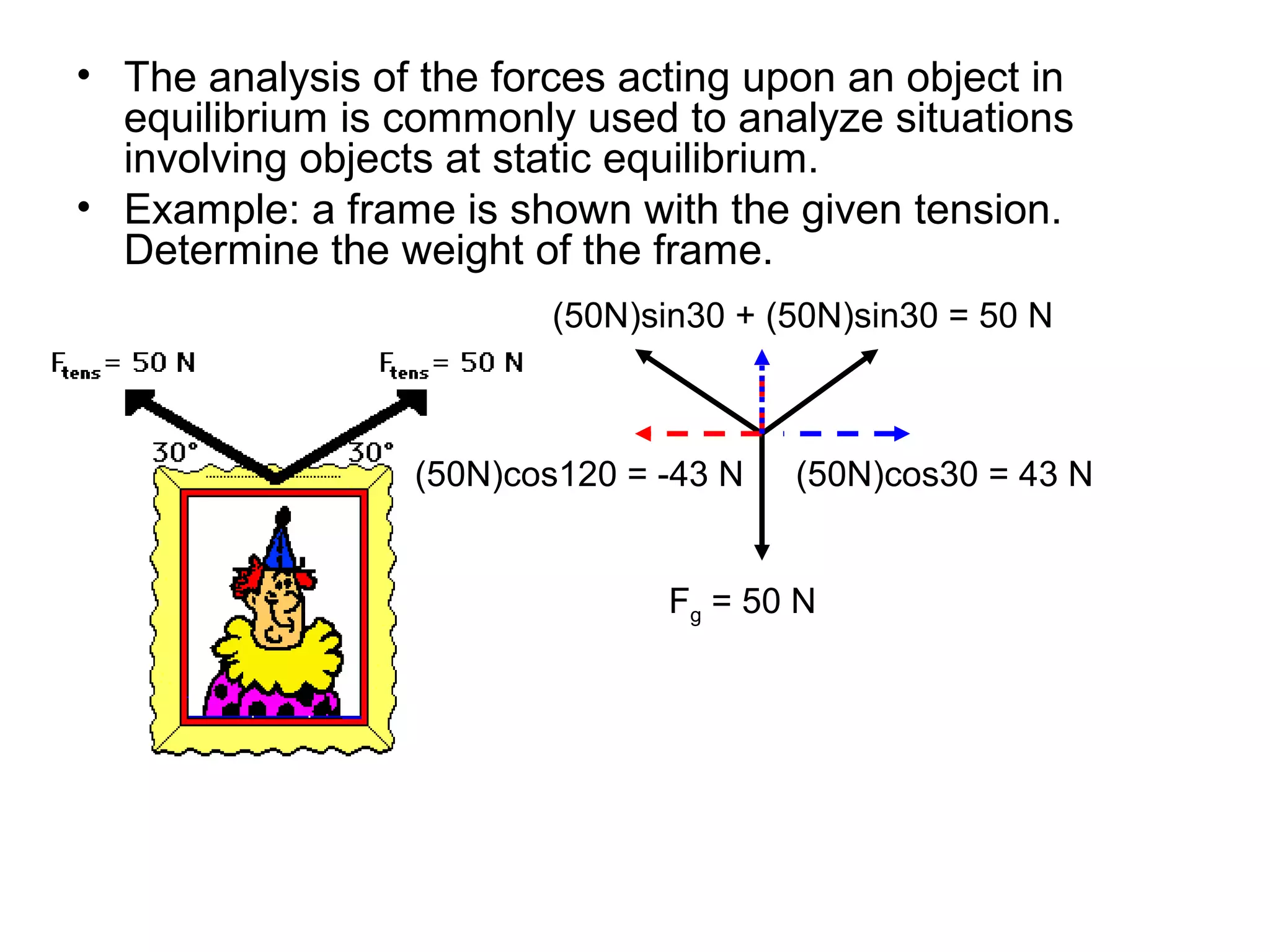
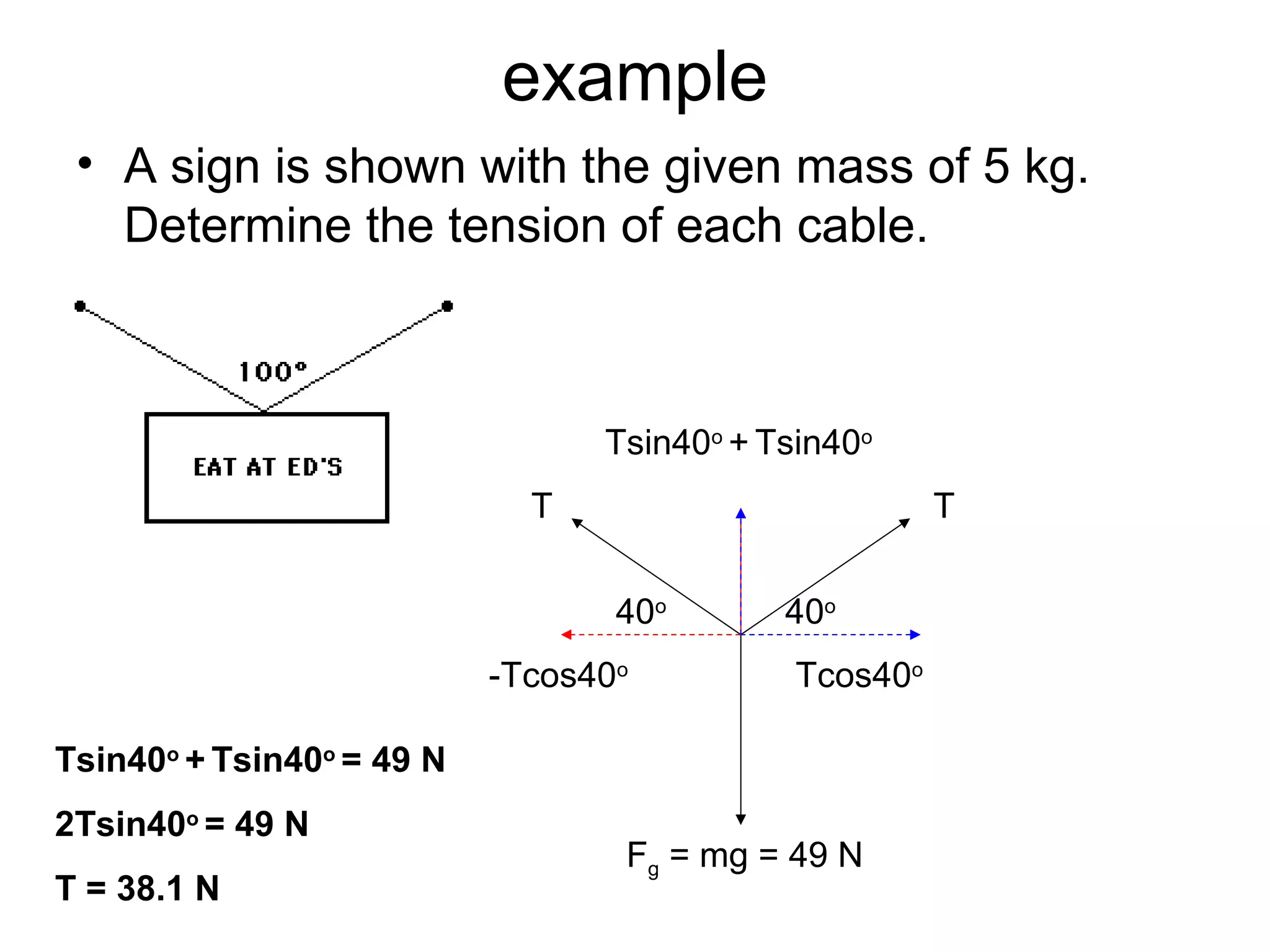
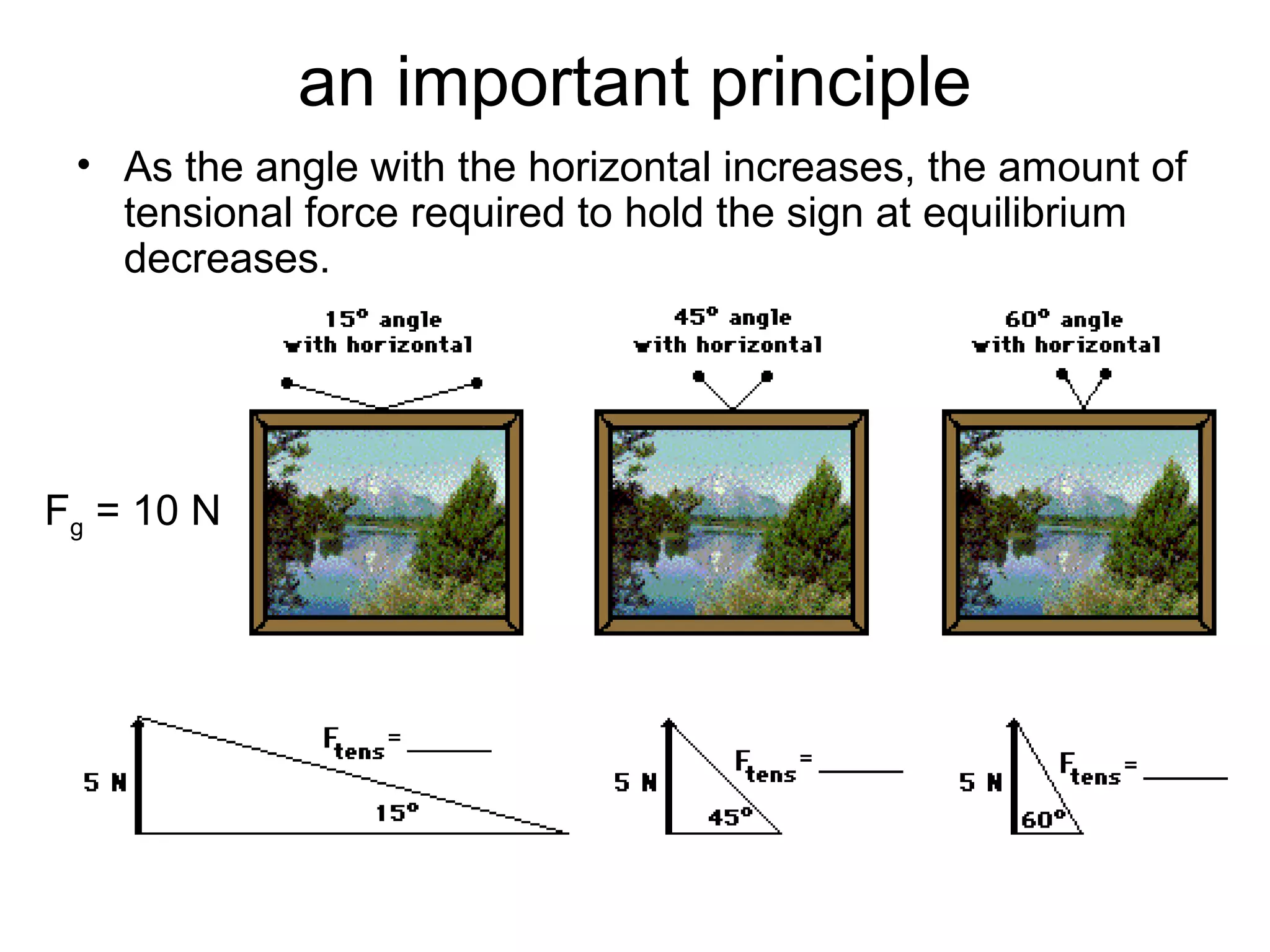
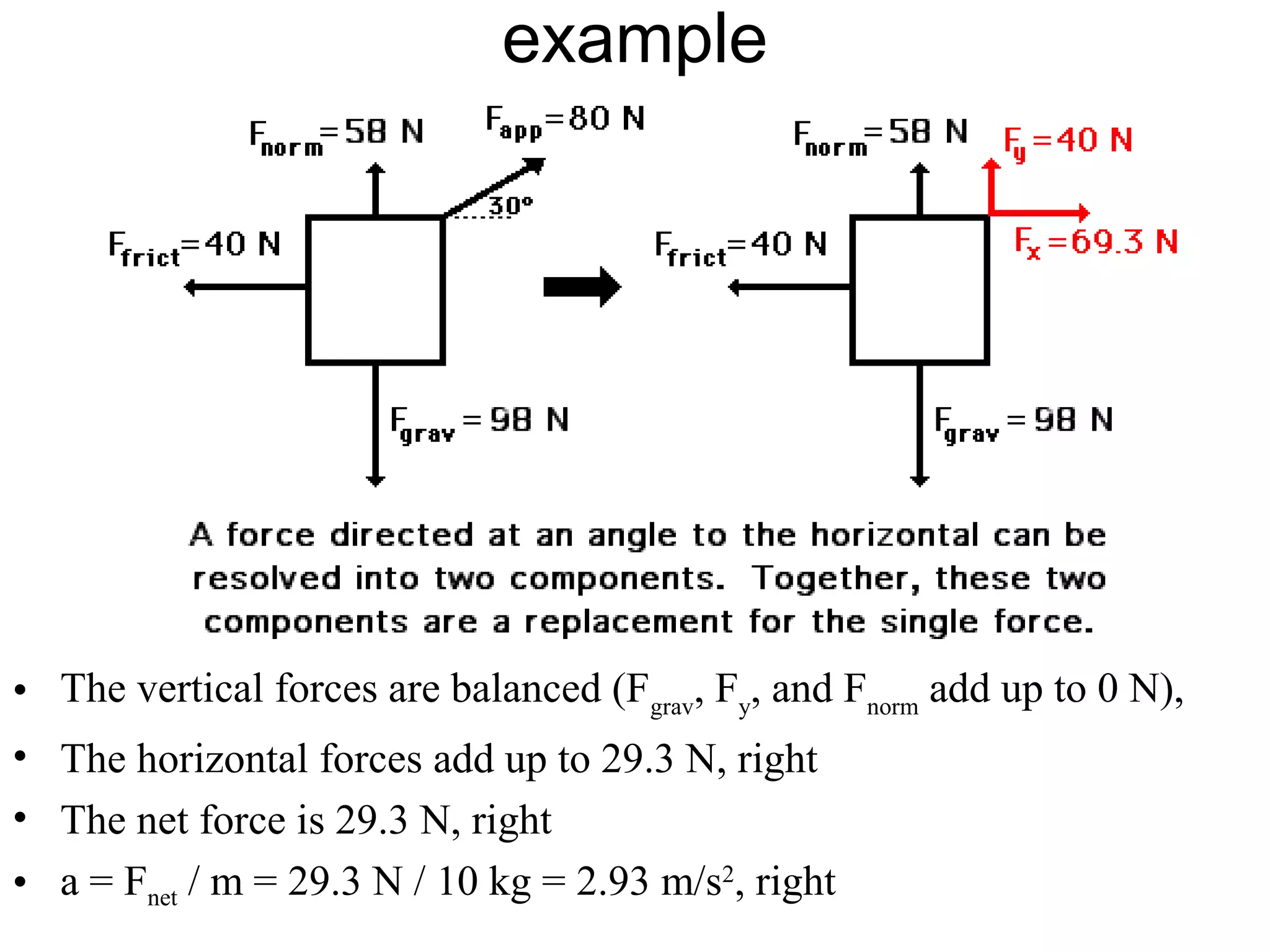
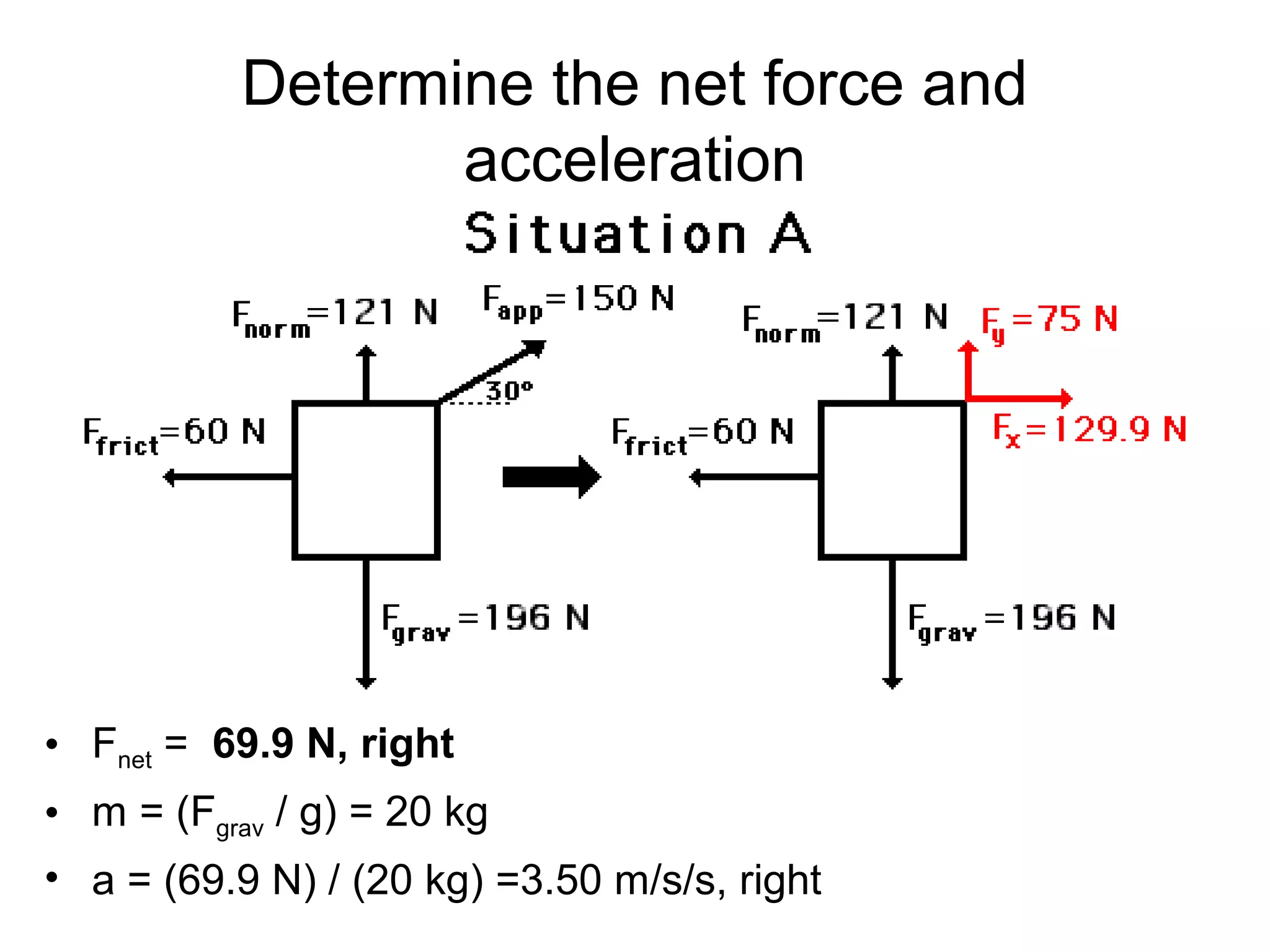
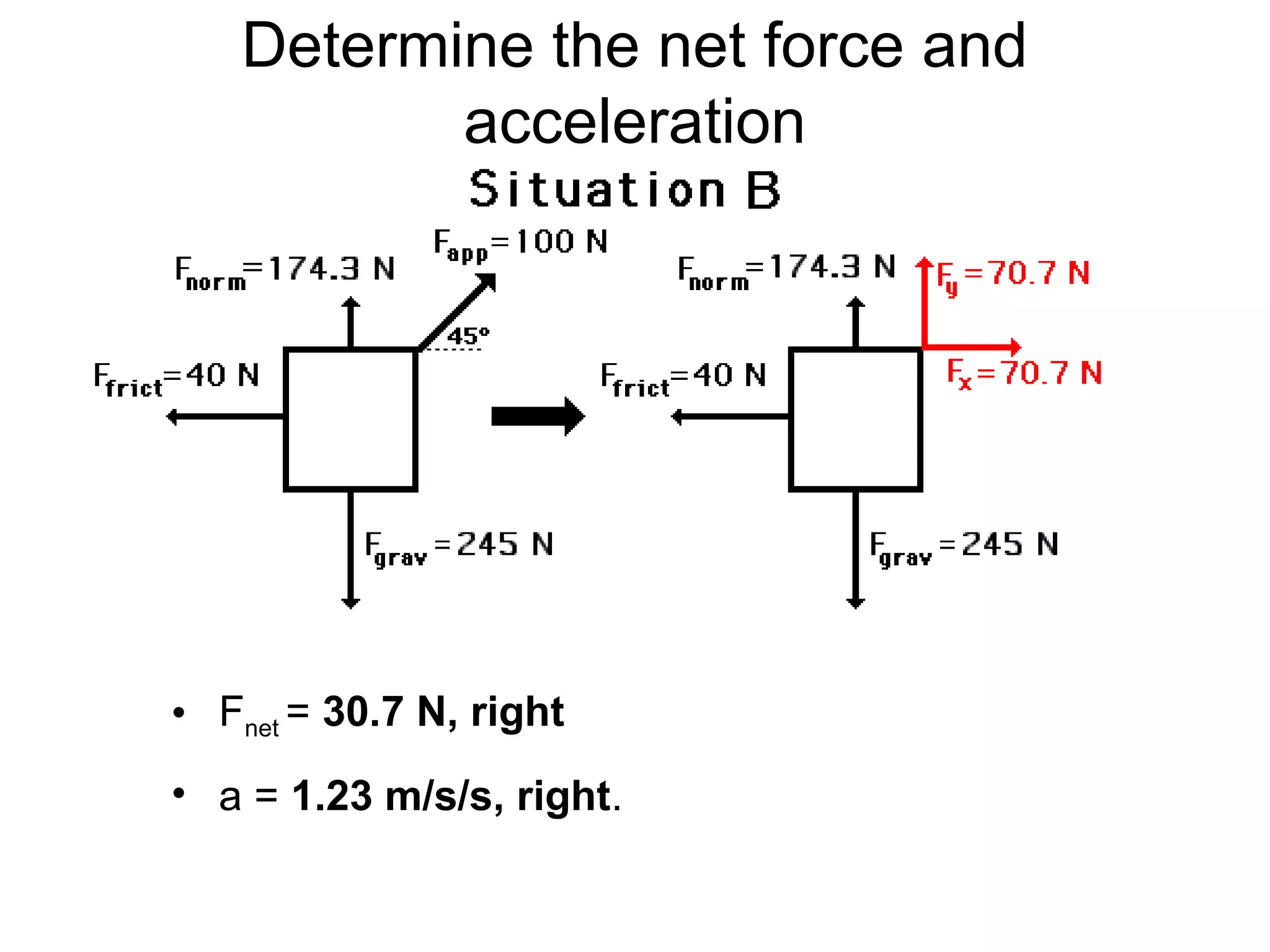
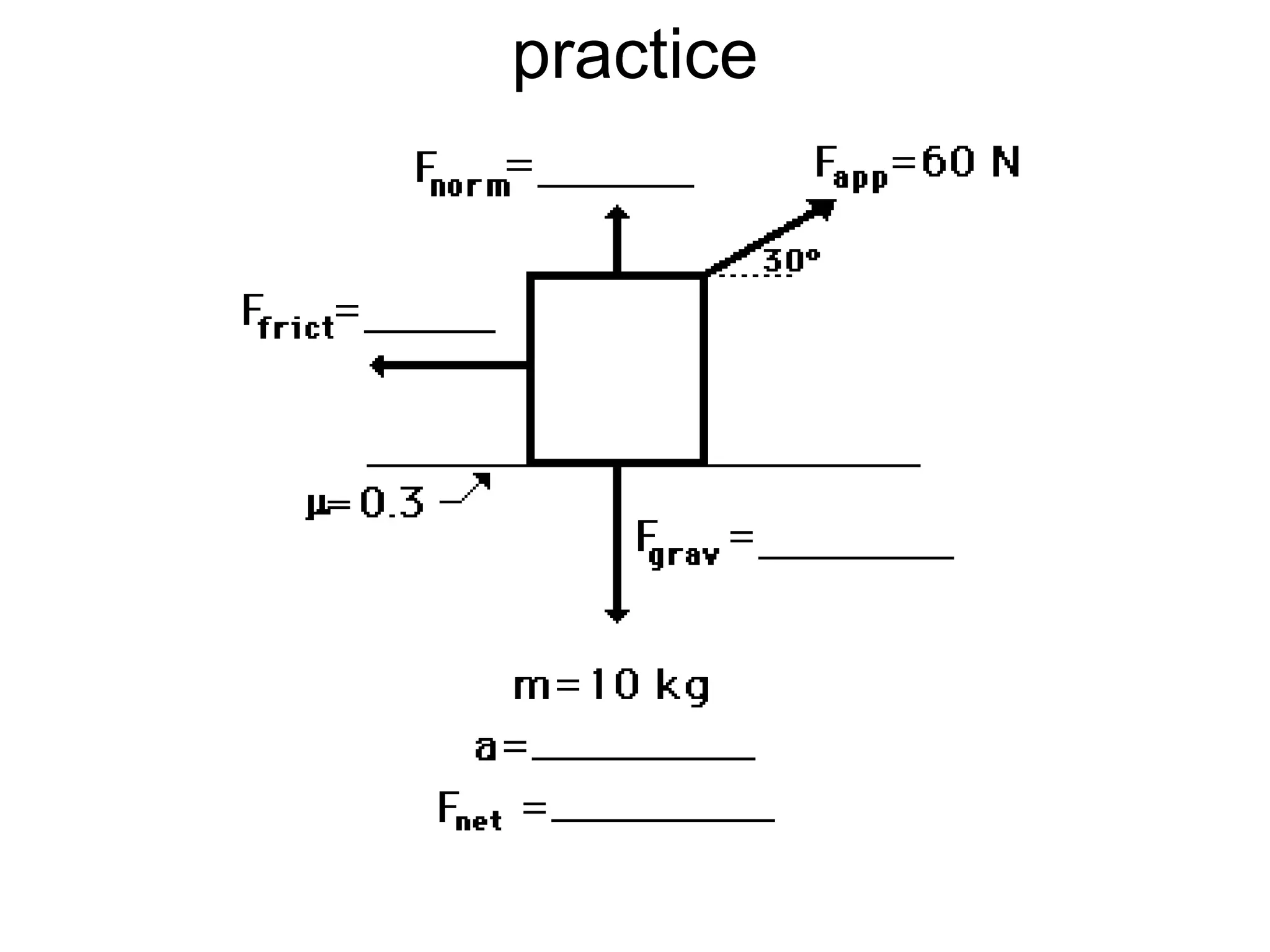
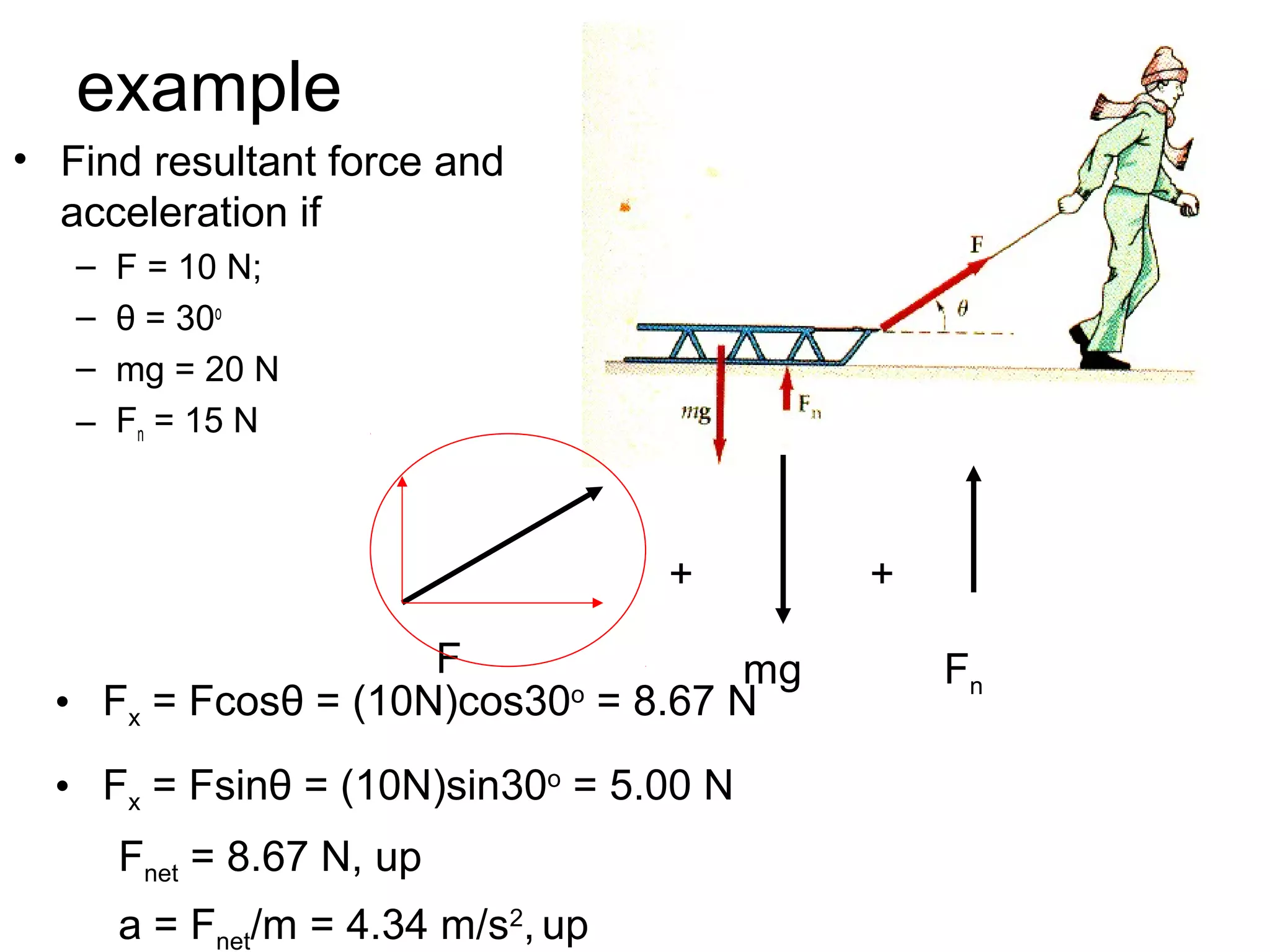
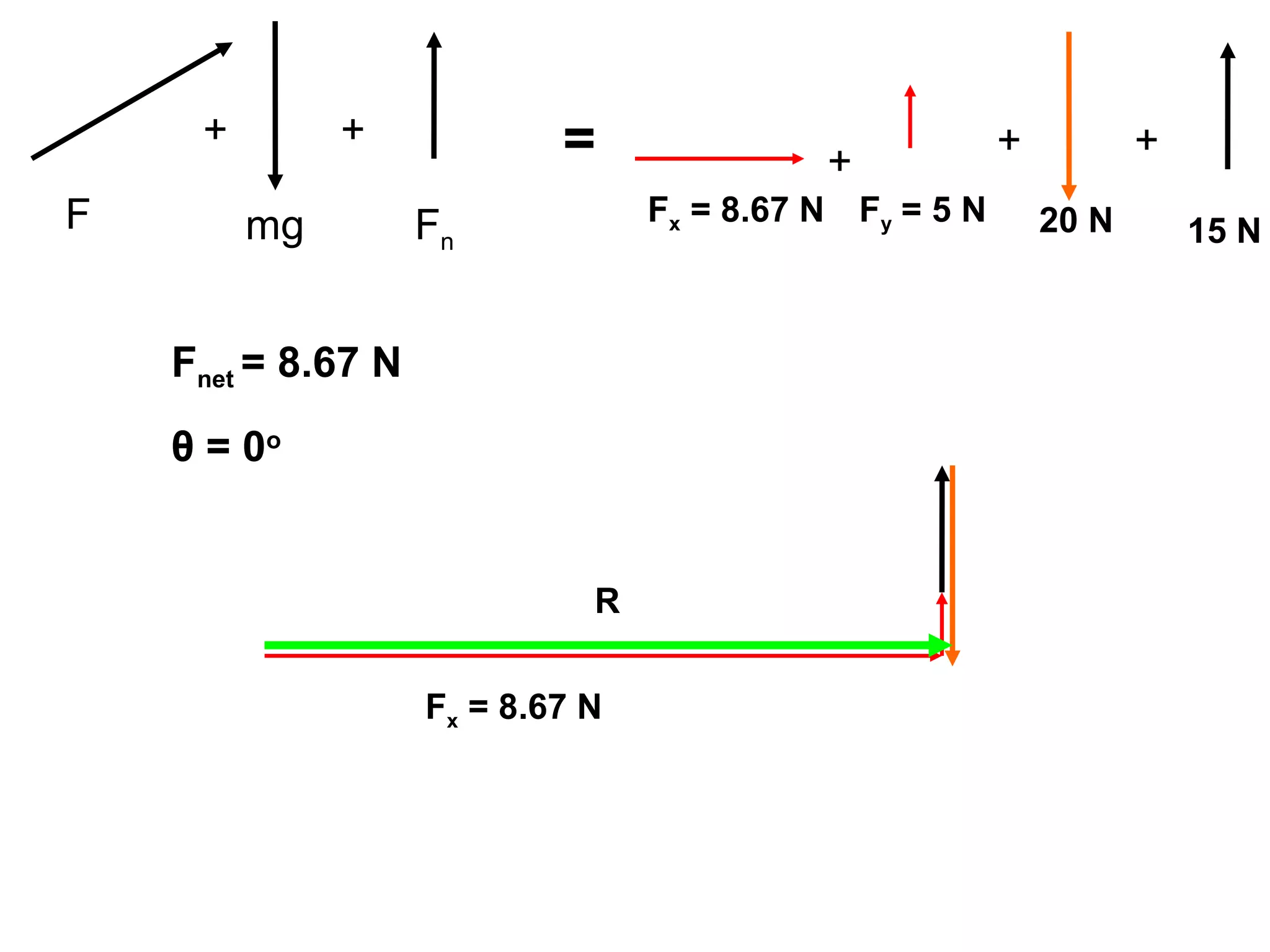
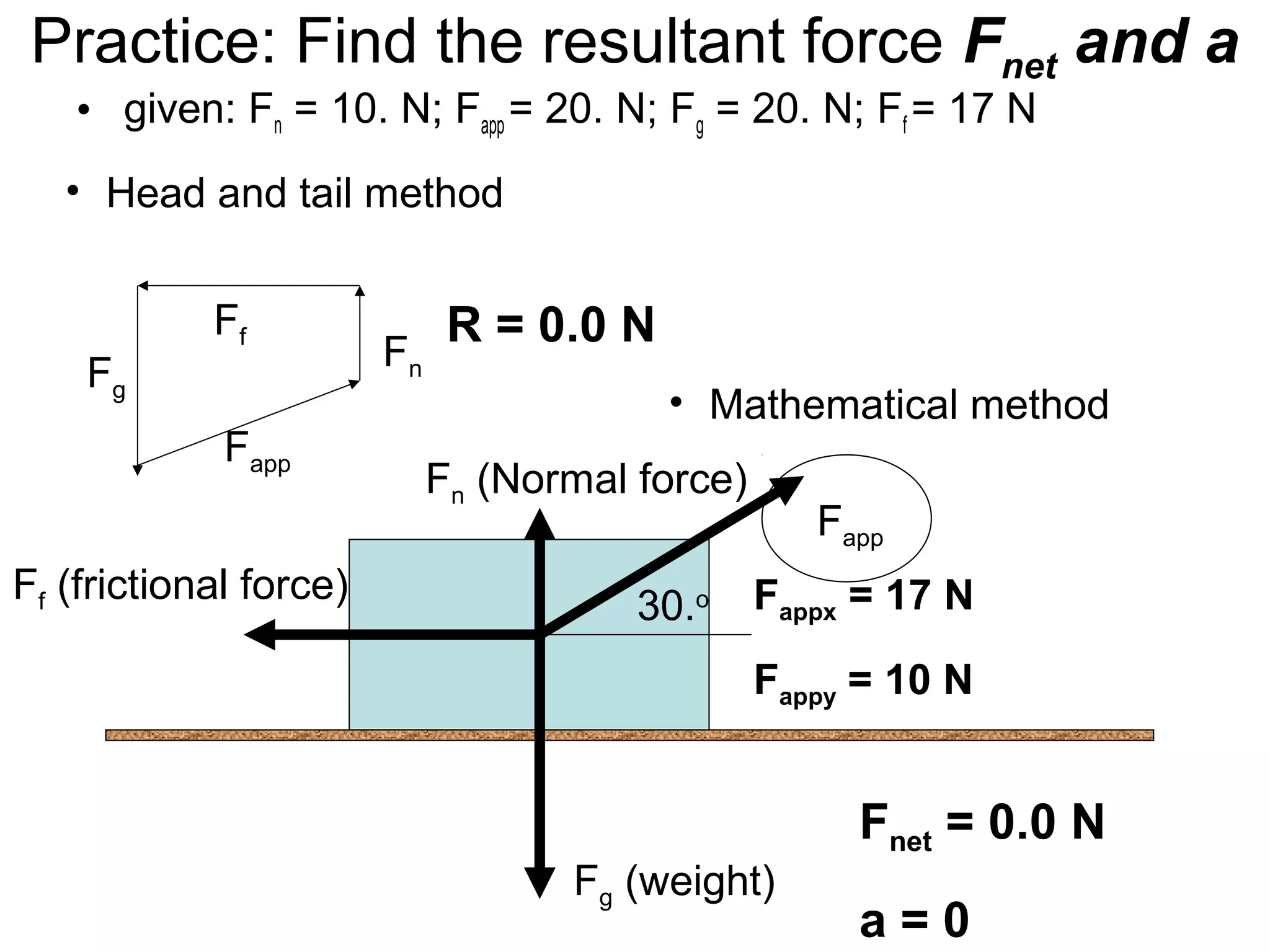
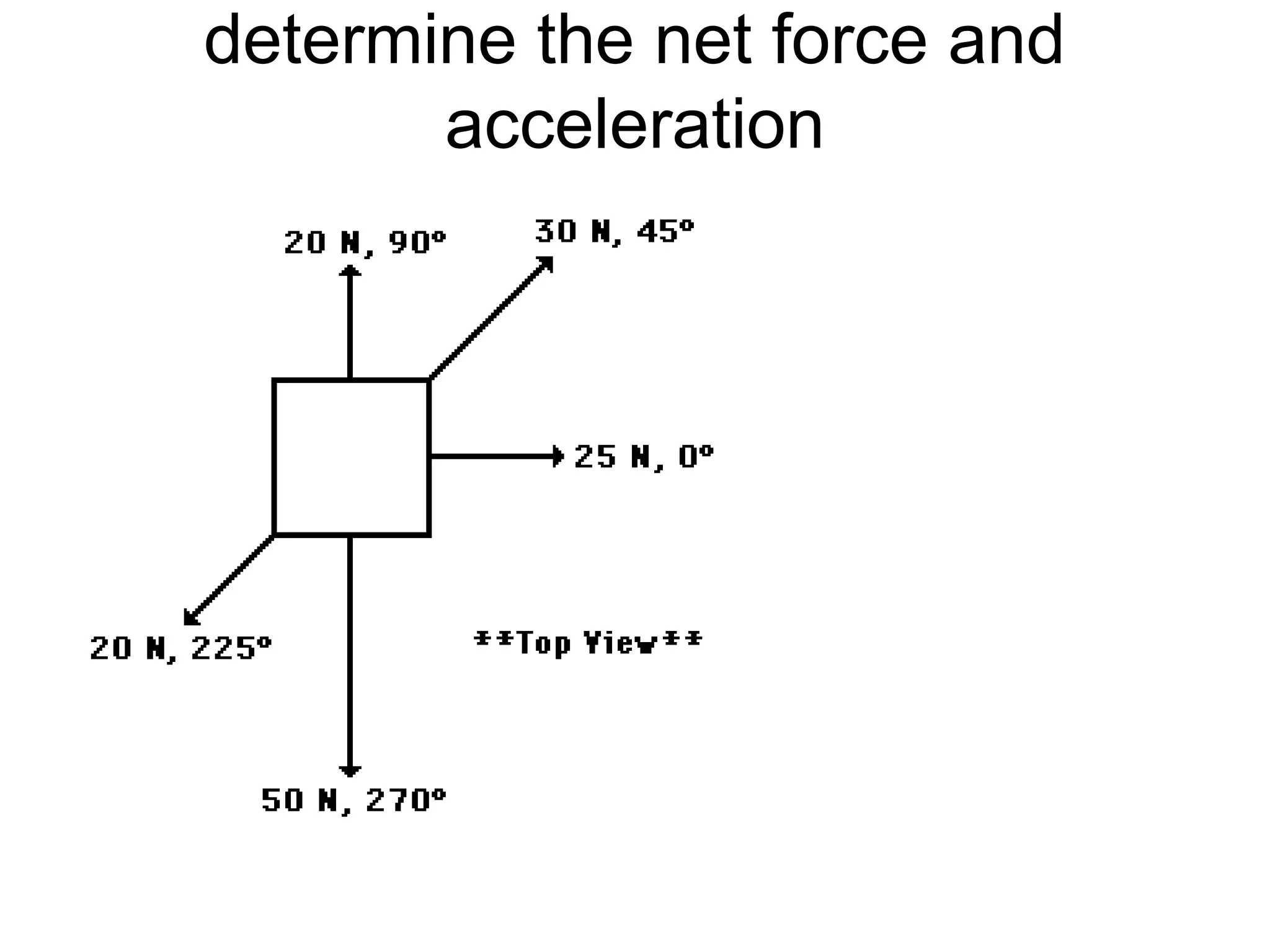
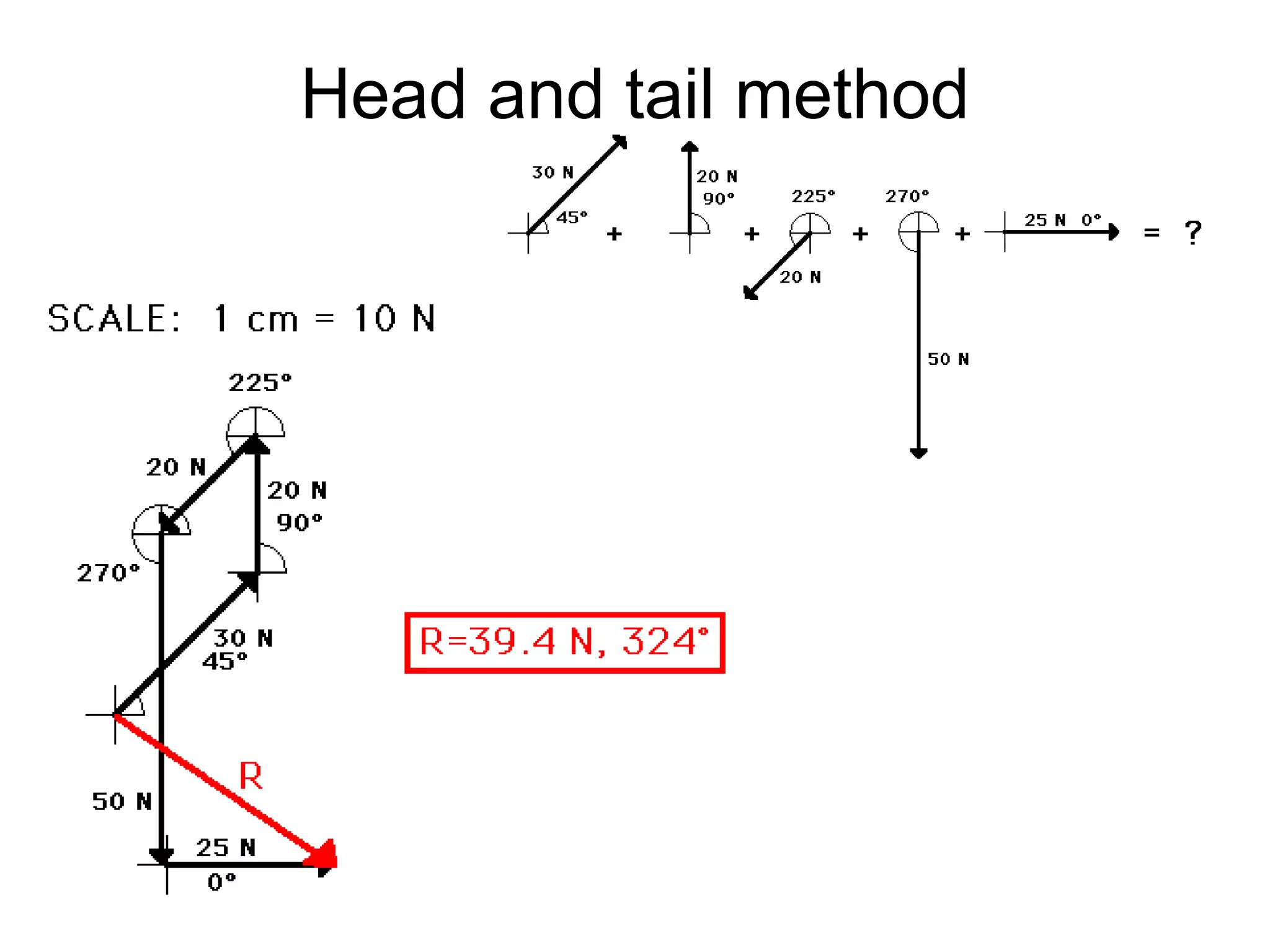
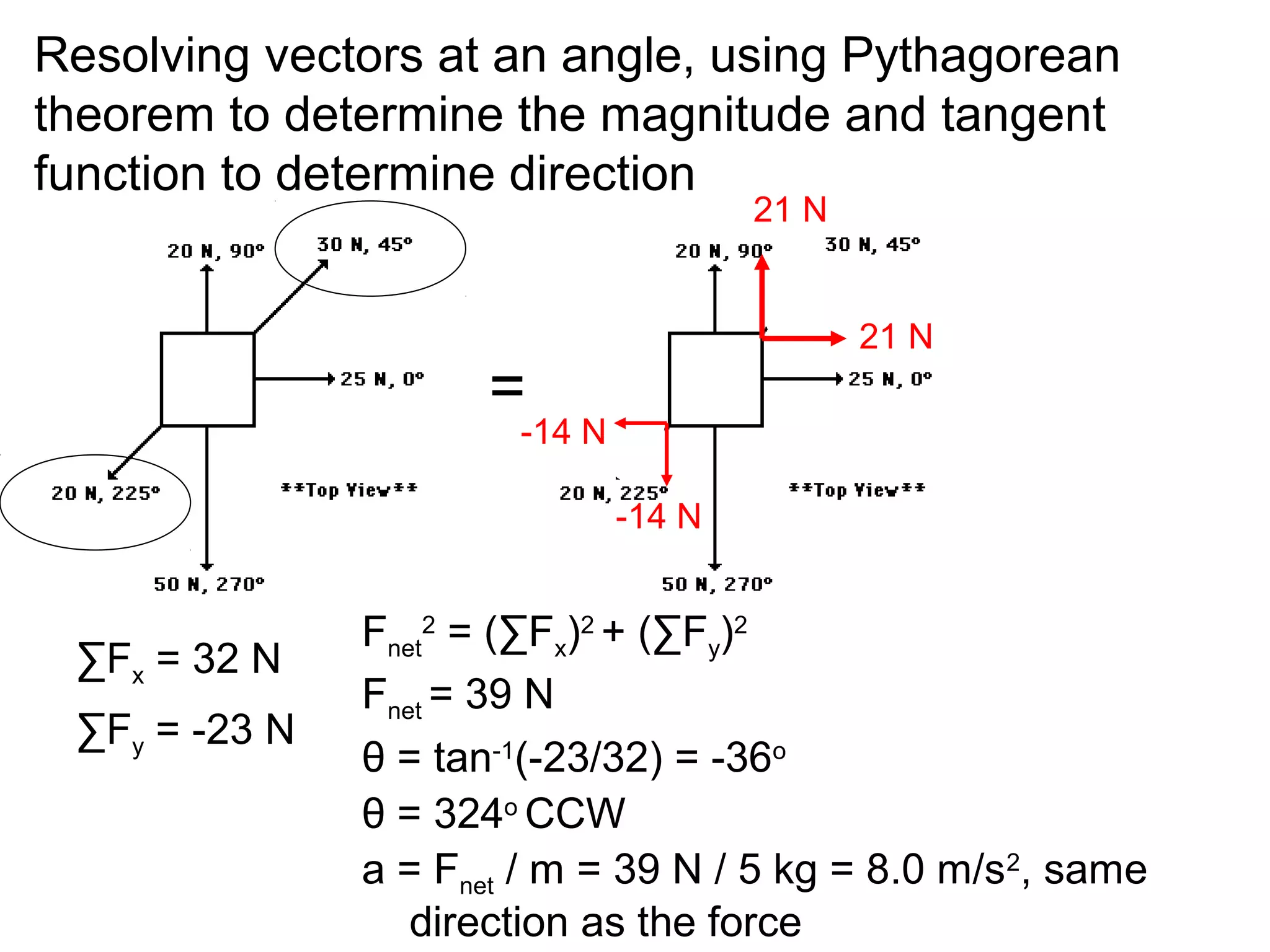
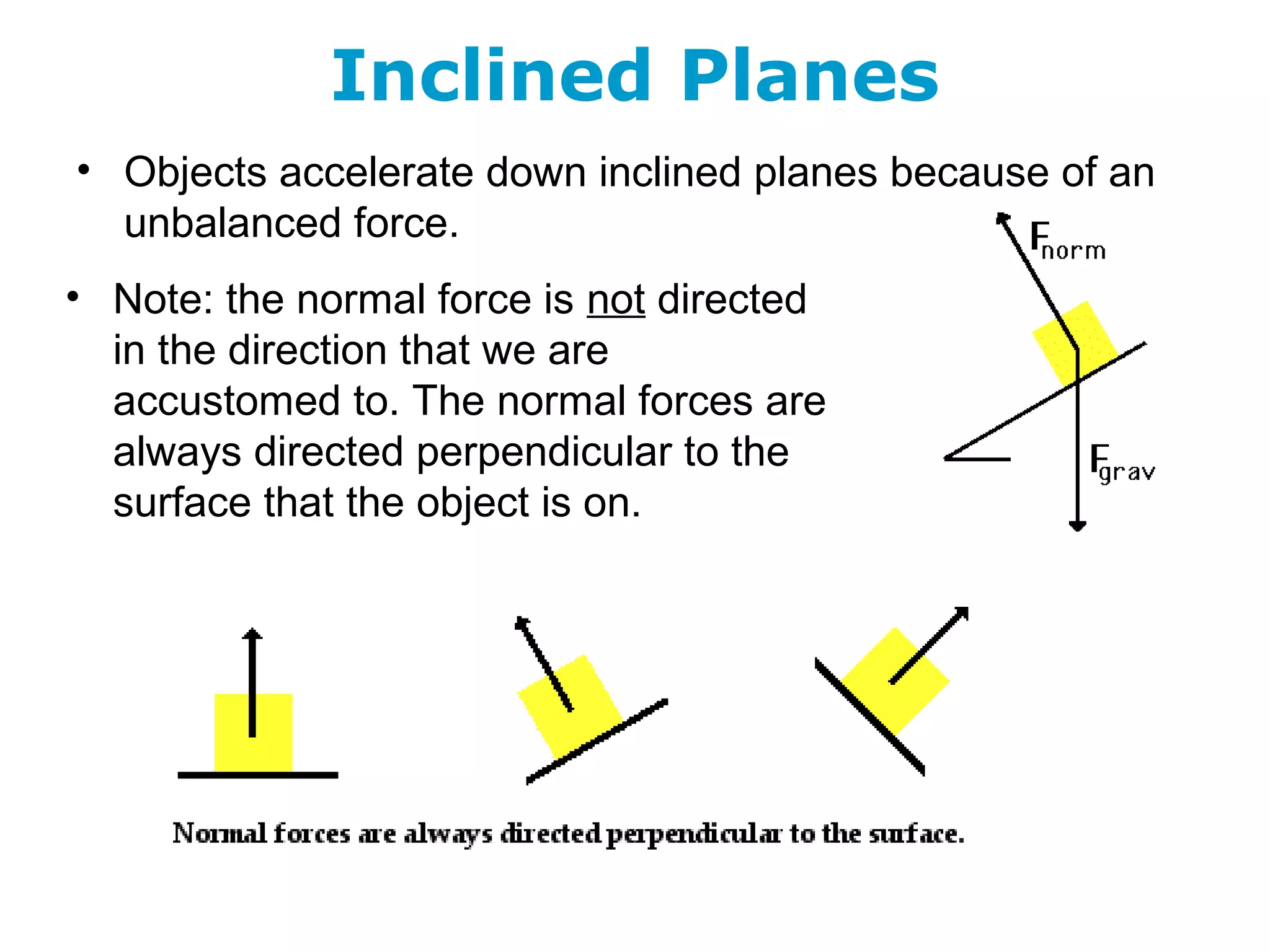
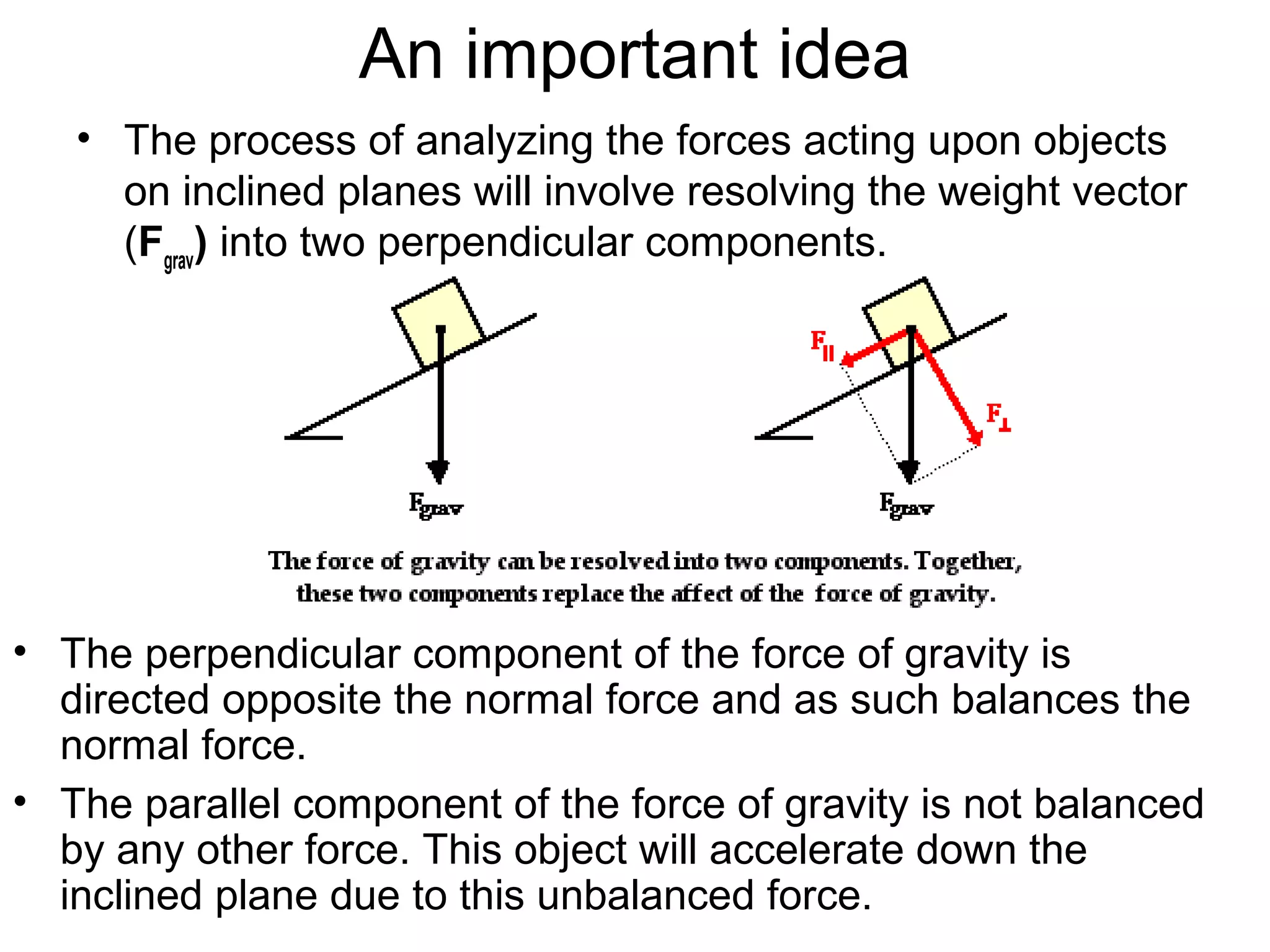
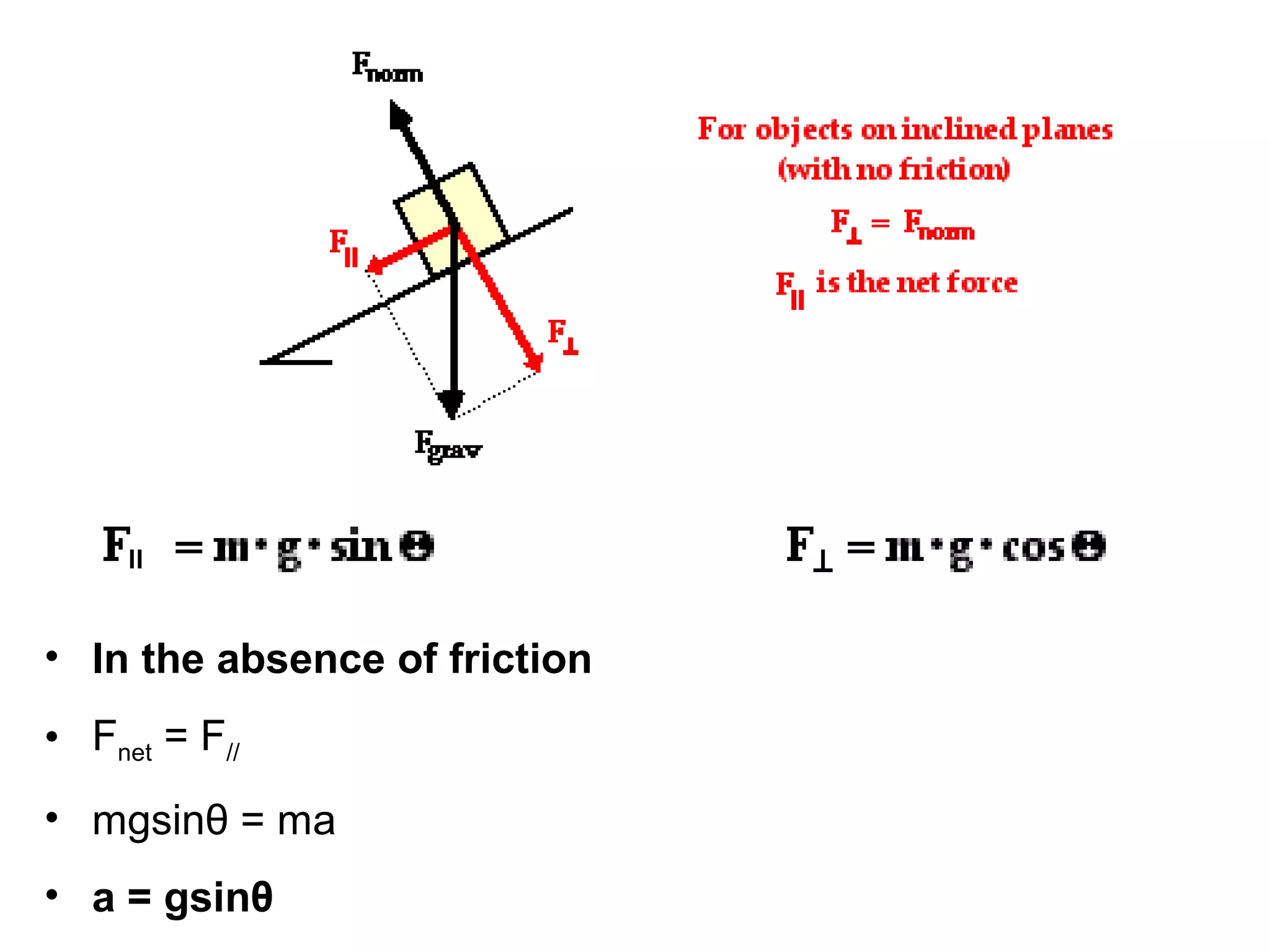
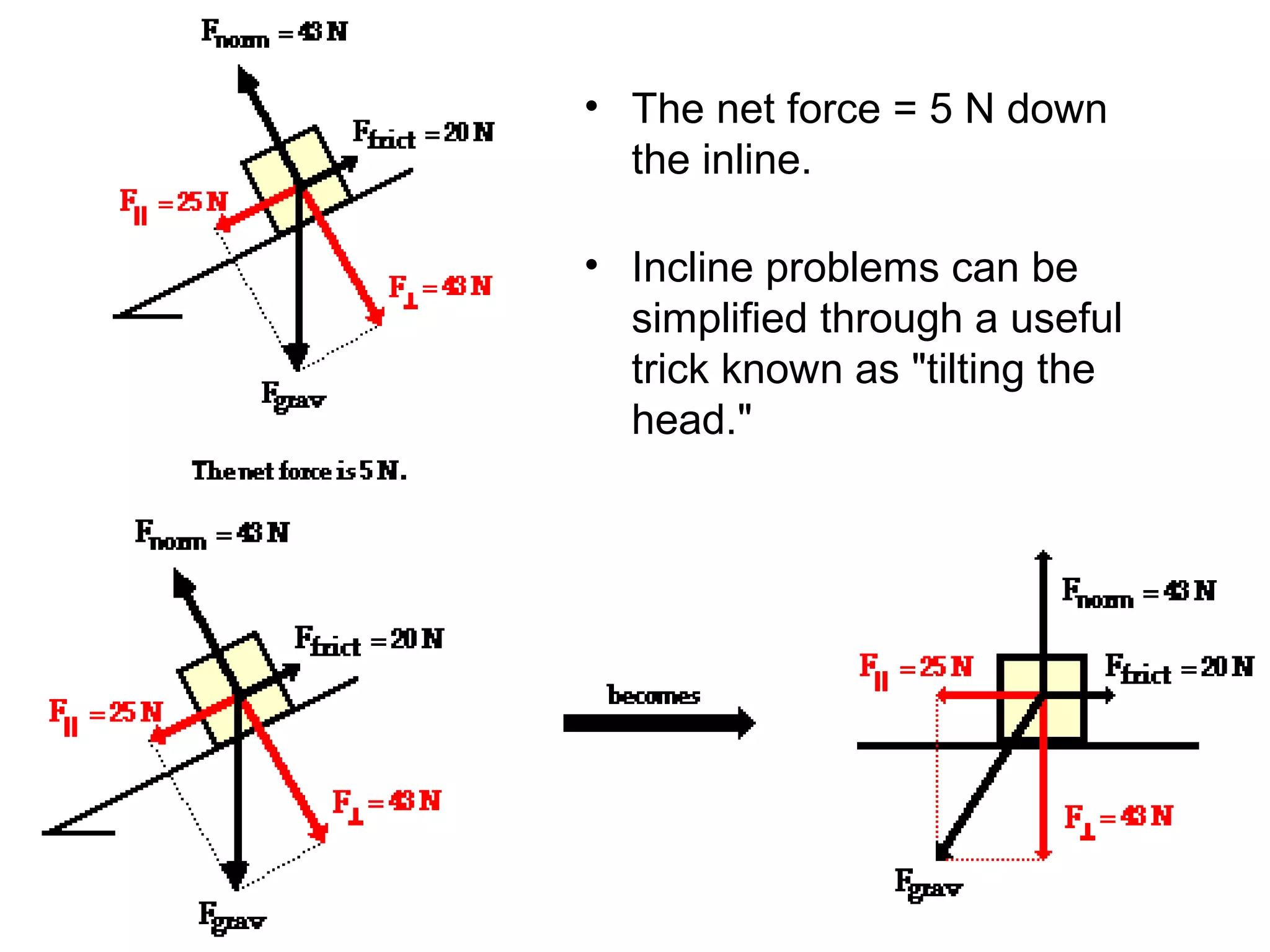
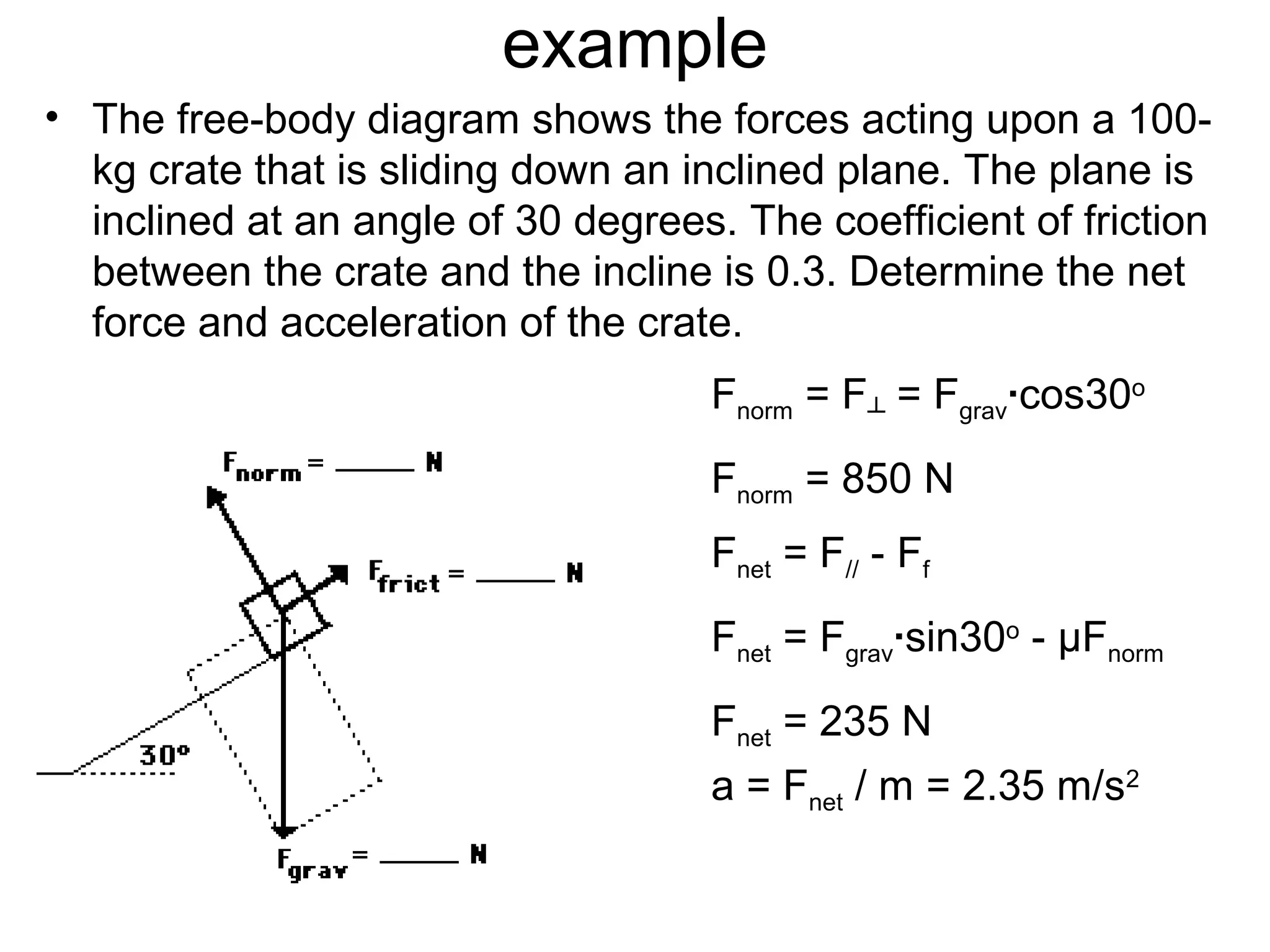
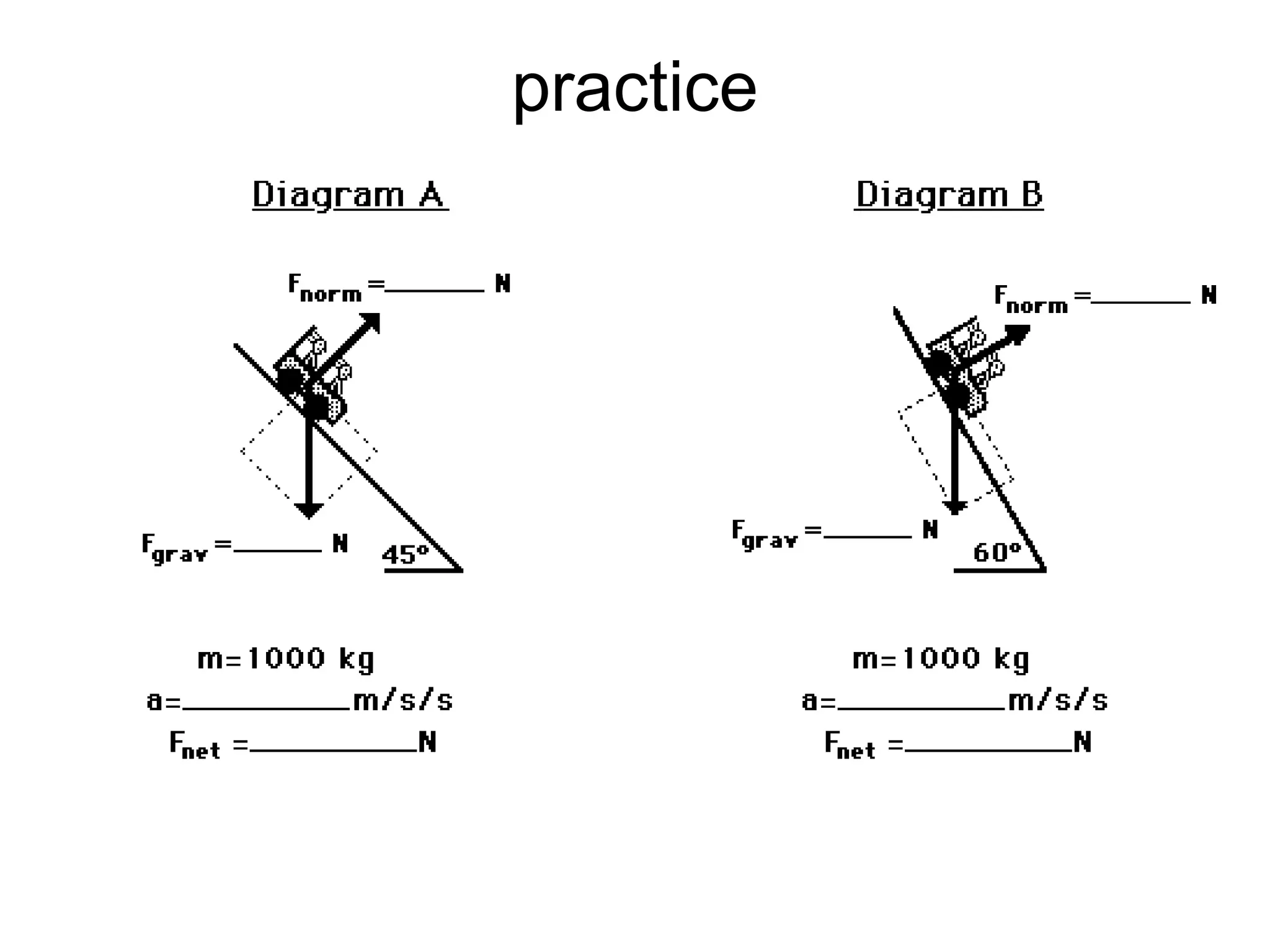
The document discusses vectors and their components, including how to add vectors using trigonometric functions or by resolving vectors into horizontal and vertical components, and it provides examples of using these methods to solve vector addition problems involving displacement, velocity, and forces. It also covers the concept of relative velocity and how to solve riverboat problems using vector addition and trigonometric functions.

1. 10/18 do now
• The mass of a space shuttle is approximately 2.0 × 106
kg. During lift-off, the net force on the shuttle is 1.0 ×
107
newtons directed upward. What is the speed of the
shuttle 10. seconds after lift-off? [Neglect air resistance
and the mass change of the shuttle.]

2. objectives
• Vectors
• Test retake must be taken by 10/28, you must
complete the following in order to retake the test
– Test corrections
– Finish castle learning test retake review
assignment
• Homework – castle learning – vector 1 – due
Wednesday
• Quiz on Friday on vectors

3. Vectors: Motion and Forces in Two
Dimensions - Chapter Outline
• Lesson 1: Vectors - Fundamentals and
Operations
• Lesson 2: Projectile Motion
• Lesson 3: Forces in Two Dimensions

4. Lesson 1: Vectors -
Fundamentals and Operations
1. Vectors and Direction
2. Vector Addition
3. Resultants
4. Vector Components
5. Vector Resolution
6. Component Method of Vector Addition
7. Relative Velocity and Riverboat Problems
8. Independence of Perpendicular Components of Mot

5. Vectors and Direction
• All quantities can by divided into two categories -
vectors and scalars.
• A vector quantity is fully described by both magnitude
and direction.
• A scalar quantity is fully described by its magnitude.
• Examples of vector include displacement, velocity,
acceleration, and force. Each of these quantities
demands both a magnitude and a direction are listed

6. • Vector quantities are often represented by scaled
vector diagrams.
• There are several characteristics of
this diagram that make it an
appropriately drawn vector diagram.
1. a scale is clearly listed
2. a vector arrow (with arrowhead) is
drawn in a specified direction. The
vector arrow has a head and a tail.
3. the magnitude and direction of the
vector is clearly labeled. In this case,
the diagram shows the magnitude is
20 m and the direction is (30 degrees
West of North).

7. Conventions for Describing
Directions of Vectors
1. The direction of a vector is often expressed as an angle of
rotation of the vector about its "tail" from east, west, north,
or south.
2. The direction of a vector is often expressed as a
counterclockwise angle of rotation of the vector about
its "tail" from due East.

8. Representing the Magnitude of a Vector
• The magnitude of a vector in a scaled
vector diagram is depicted by the length of
the arrow. The arrow is drawn a precise
length in accordance with a chosen scale.

9. practice
• Determine the magnitudes and directions
of vectors

10. 10/19 do now
• Vector practice packet
• Page 1 #4, 5, 6
• Page 2 #8, 9

11. 10/20 do now
• What is the magnitude of the force needed to keep a
60.-newton rubber block moving across level, dry
asphalt in a straight line at a constant speed of 2.0
meters per second?

12. objectives
1. Vector Addition
2. Resultants
3. Vector Components
4. Vector Resolution
• Test retake must be taken by 10/28, you must complete
the following in order to retake the test
•Test corrections
•Finish castle learning test retake review
assignment
• Homework – castle learning – vector 2

13. Vector Addition
• Two vectors can be added together to determine
the result (or resultant).
• The two methods
used throughout
the entire unit are:
1. the Pythagorean
theorem and
trigonometric
methods
2. the head-to-tail
method using a
scaled vector
diagram

14. The Pythagorean Theorem
• Example: Eric leaves the base camp and hikes 11 km,
north and then hikes 11 km east. Determine Eric's
resulting displacement.
• The procedure is restricted to
the addition of two vectors that
make right angles to each
other.

16. Using Trigonometry to Determine
a Vector's Direction
• Example: Eric leaves the base
camp and hikes 11 km, north and
then hikes 11 km east. Determine
Eric's overall resulting
displacement.

17. • Note: The measure of an angle as determined through
use of SOH CAH TOA is not always the direction of the
vector.

19. Use of Scaled Vector Diagrams to
Determine a Resultant
• The magnitude and direction of the sum of two or more
vectors can also be determined by use of an accurately
drawn scaled vector diagram. Using a scaled diagram,
the head-to-tail method is employed to determine the
vector sum or resultant.

20. • applying the head-to-tail method to determine the sum of two
or more vectors:
1. Choose a scale and indicate it on a sheet of paper. The best
choice of scale is one that will result in a diagram that is as
large as possible, yet fits on the sheet of paper.
2. Pick a starting location and draw the first vector to scale in the
indicated direction. Label the magnitude and direction of the
scale on the diagram (e.g., SCALE: 1 cm = 20 m).
3. Starting from where the head of the first vector ends, draw the
second vector to scale in the indicated direction. Label the
magnitude and direction of this vector on the diagram.
4. Repeat steps 2 and 3 for all vectors that are to be added
5. Draw the resultant from the tail of the first vector to the head
of the last vector. Label this vector as Resultant or simply R.
6. Using a ruler, measure the length of the resultant and
determine its magnitude by converting to real units using the
scale (4.4 cm x 20 m/1 cm = 88 m).
7. Measure the direction of the resultant using the
counterclockwise convention.

21. • Note: the order in which
three vectors are added has
no affect upon either the
magnitude or the direction
of the resultant. The
resultant will still have the
same magnitude and
direction.

22. Resultants
• The resultant is the vector sum of two or
more vectors. It is the result of adding two
or more vectors together.

23. practice
• Vector addition – head and tail method

24. 10/20 do now
• What is the magnitude of the force needed to keep a
60.-newton rubber block moving across level, dry
asphalt in a straight line at a constant speed of 2.0
meters per second?

25. objectives
1. Vector Components
2. Vector Resolution
• Test retake must be taken by 10/28, you must complete
the following in order to retake the test
•Test corrections
•Finish castle learning test retake review
assignment
• Homework – castle learning – vector 3

26. Vector addition

27. Practice: determine resultant

28. Determine resultant
A
B
B
A
B
A
90o
0o
180o
The sum of any two vectors A & B can have a
maximum value of (|A| + |B|) and minimum
value of | |A| - |B| |.

29. example
• A 5.0-newton force and a 7.0-newton force
act concurrently on a point. As the angle
between the forces is increased from 0° to
180°, the magnitude of the resultant of the
two forces changes from
1. 0.0 N to 12.0 N
2. 2.0 N to 12.0 N
3. 12.0 N to 2.0 N
4. 12.0 N to 0.0 N

30. example
• A 3-newton force and a 4-newton force are
acting concurrently on a point. Which force
could not produce equilibrium with these two
forces?
1. 1 N
2. 7 N
3. 9 N
4. 4 N

31. example
• As the angle between two concurrent
forces decreases, the magnitude of the
force required to produce equilibrium
1. decreases
2. increases
3. remains the same

32. Vector Components
• In situations in which vectors are directed at angles to
the customary coordinate axes, a useful mathematical
trick will be employed to transform the vector into two
parts with each part being directed along the coordinate
axes.

33. • Any vector directed in two dimensions can be thought of as
having an influence in two different directions.
• Each part of a two-dimensional vector is known as a
component.
• The components of a vector depict the influence of that
vector in a given direction.
• The combined influence of the two components is
equivalent to the influence of the single two-dimensional
vector.
• The single two-dimensional vector could be replaced by the
two components.

34. 10/21 do now
• A horizontal force is used to pull a 5.0-kilogram cart at a
constant speed of 5.0 meters per second across the
floor, as shown in the diagram. If the force of friction
between the cart and the floor is 10. newtons, what is
the magnitude of the horizontal force along the handle of
the cart?

35. objectives
• Vector resolution
• Component Method of Vector
Addition
• quiz
• Lab
• Newton’s laws practice packet
• Homework – castle learning – vector 4

36. Vector Resolution
• Any vector directed in two dimensions
can be thought of as having two
components.
• The two basic methods for determining
the magnitudes of the components of a
vector directed in two dimensions are
1. the parallelogram method
2. the trigonometric method

37. Parallelogram Method of Vector
Resolution
• The parallelogram method of vector resolution
involves:
1. drawing the vector to scale in the indicated
direction,
2. sketching a parallelogram around the vector
such that the vector is the diagonal of the
rectangle,
3. determining the magnitude of the components
(the sides of the rectangle) using the scale.

39. Trigonometric Method of Vector
Resolution
• The method of employing trigonometric functions to
determine the components of a vector are as follows:
1. Construct a rough sketch (no scale needed) of the
vector in the indicated direction. Draw a rectangle about
the vector such that the vector is the diagonal of the
rectangle.
2. Label the components of the vectors with symbols to
indicate which component represents which side.
3. To determine the length of the side opposite the
indicated angle, use the sine function. Substitute the
magnitude of the vector for the length of the hypotenuse.
4. Repeat the above step using the cosine function to
determine the length of the side adjacent to the indicated
angle.

40. Fvert = (60 N)·sin40o
= 38.6 N
Fhoriz = (60 N)·cos40o
= 45.9 N

41. 10/24 do now
• Vector practice packet - Page 5, 6

42. 10/25 do now
• A hockey player accelerates a puck (m = 0.167 kg) from
rest to a velocity of 50 m/s in 0.0121 sec.
1. Determine the acceleration of the puck
2. Determine the force applied by the hockey stick to the
puck.
4132 m/s/s
690 N

43. objectives
• Component Method of Vector
Addition
Vector addition
homework

44. Component Method of
Vector Addition
• In order to solve more complex vector addition problems,
we need to combine the concept of vector components
and the principles of vector resolution with the use of the
Pythagorean theorem.

45. Addition of Three or More Right
Angle Vectors
R2
= (8.0 km)2
+ (6.0 km)2
R2
= 64.0 km2
+ 36.0 km2
R2
= 100.0 km2
R = SQRT (100.0 km2
)
R = 10.0 km
• Add
horizontal
components
• Add vertical
components

46. SOH CAH TOA and the Direction of
Vectors
• The tangent function will be used to
calculate the angle measure of theta (Θ).
Tangent(Θ) = Opposite/Adjacent
Tangent(Θ) = 8.0/6.0
Θ =53°
• Since the angle that the resultant makes
with east is the complement of the angle
that it makes with north, we could express
the direction as 53° CCW.

47. R2
= (22.0 m)2
+ (52.0 m)2
R2
= 484.0 m2
+ 2704.0 m2
R2
= 3188.0 m2
R = SQRT (3188.0 m2
)
R = 56.5 m
• The resultant of the
addition of three or
more right angle
vectors can be easily
determined using the
Pythagorean theorem
2 m
16 m 24 m 36 m

48. • The CCW direction is 157.1° CCW.

49. Addition of Non-Perpendicular
Vectors
Vector A has two components - Ax
and Ay
.

50. Procedures for adding vectors at an
angle with horizontal
1. Resolve the vectors at an angle into x
and y components.
2. Add all the x components together
3. Add all the y components together
4. Use Pythagorean Theorem to find the
resultant (hypotenuse)
5. Resultant2
= x2
+ y2
6. Use trigonometric function to determine
the direction: tanθ = opp / adj

51. example
A bus heads 6.00 km east, then 3.5 km north, then
1.50 km at 45o
south of west. What is the total
displacement?
A: 6.0 km, 0° CCW
B: 3.5 km, 90° CCW
C: 1.5 km, 225° CCW
BA
+
C
+
Cx = Ccos225o
= -1.06 km
Cy = Csin225o
= - 1.06 km

52. =
BA
+
C
+
BA
+
C
+ +
A+Cx = 4.94 km
B+Cy = 2.44 km
R
R = 5.5 km
tanθ = 2.44 km/4.92 km
θ=26.4o
CCW
θ

53. 10/25 do now
Add the following vectors and determine the resultant.
5.0 m/s, 45 deg and 2.0 m/s, 180 deg

54. objectives
• Hand in homework
• Relative velocity and river boat problem
• Homework – hand out – due tomorrow

55. Example
• Cameron and Baxter are on a hike. Starting from home
base, they make the following movements.
A: 2.65 km, 140° CCW
B: 4.77 km, 252° CCW
C: 3.18 km, 332° CCW
• Determine the magnitude and direction of their overall
displacement.

56. Vector X Component (km) Y Component
A
2.65 km
140° CCW
(2.65 km)•cos(140°)
= -2.030
(2.65 km)•sin(140°)
= 1.703
B
4.77 km
252° CCW
(4.77 km)•cos(252°)
= -1.474
(4.77 km)•sin(252°)
= -4.536
C
3.18 km
332° CCW
(3.18 km)•cos(332°)
= 2.808
(3.18 km)•sin(332°)
= -1.493
Sum of
A + B + C
-0.696 -4.326

57. R2
= (-0.696 km)2
+ (-4.326 km)2
R2
= 0.484 km2
+ 18.714 km2
R2
= 19.199 km2
R = SQRT(19.199 km2
)
R = 4.38 km
Tangent(Θ) = opposite/adjacent
Tangent(Θ) = (-4.326 km)/(-0.696 km)
Tangent(Θ) = 6.216
Θ = tan-1
(6.216)
Θ = 80.9°
direction of 260.9° (CCW).

58. Relative Velocity and
Riverboat Problems
• On occasion objects move
within a medium that is
moving with respect to an
observer.

61. 100 km/hr)2
+ (25 km/hr)2
= R2
10 000 km2
/hr2
+ 625 km2
/hr2
= R2
10 625 km2
/hr2
= R2
SQRT(10 625 km2
/hr2
) = R
103.1 km/hr = R
tan(θ) = (opposite/adjacent)
tan (θ) = (25/100)
θ = tan-1
(25/100)
θ = 14.0o
– CCW 256o

62. Analysis of a Riverboat's Motion
• The affect of the wind upon the plane is similar to the
affect of the river current upon the motorboat.

63. • Suppose that the river was moving with a velocity of 3
m/s, North and the motorboat was moving with a
velocity of 4 m/s, East. What would be the resultant
velocity of the motorboat (i.e., the velocity relative to an
observer on the shore)?
(4.0 m/s)2
+ (3.0 m/s)2
= R2
16 m2
/s2
+ 9 m2
/s2
= R2
25 m2
/s2
= R2
SQRT (25 m2
/s2
) = R
5.0 m/s = R
tan(θ) = (opposite/adjacent)
tan(θ) = (3/4)
θ = tan-1
(3/4)
θ = 36.9o

64. • Motorboat problems such as these are typically
accompanied by three separate questions:
1.What is the resultant velocity (both magnitude
and direction) of the boat?
2.If the width of the river is X meters wide, then
how much time does it take the boat to travel
shore to shore?
3.What distance downstream does the boat
reach the opposite shore?

65. Example 1
• A motorboat traveling 4 m/s, East
encounters a current traveling 3.0 m/s,
North.
1. What is the resultant velocity of the
motorboat?
2. If the width of the river is 80 meters wide,
then how much time does it take the boat to
travel shore to shore?
3. What distance downstream does the boat
reach the opposite shore?
5 m/s at 36.9 degrees

66. 2. If the width of the river is 80 meters wide,
then how much time does it take the boat to
travel shore to shore?
time = distance /(ave. speed) 5 m
/s
80 m
time = (80 m)/(4 m/s) = 20 s

67. 3. What distance downstream does the
boat reach the opposite shore?
distance = ave. speed * time
distance = = (3 m/s) * (20 s)
distance = 60 m
5 m
/s
d

68. Example 2
• A motorboat traveling 4 m/s, East encounters a current
traveling 7.0 m/s, North.
1. What is the resultant velocity of the motorboat?
2. If the width of the river is 80 meters wide, then how much
time does it take the boat to travel shore to shore?
3. What distance downstream does the boat reach the
opposite shore?
a. R = 8.06 m/s; θ = 60°
b. t = d / v = (80 m) / (4 m/s) = 20 s
c. d = v • t = (7 m/s) • (20 s) = 140 m

69. Independence of Perpendicular
Components of Motion
• Any vector - whether it is a force vector, displacement
vector, velocity vector, etc. - directed at an angle can be
thought of as being composed of two perpendicular
components. These two components can be represented
as legs of a right triangle formed by projecting the vector
onto the x- and y-axis.

70. • The two perpendicular parts or components of a vector
are independent of each other.

72. Class work
• Practice packet

73. 10/27 do now
• Mia Ander exits the front door of her home and walks along
the path shown in the diagram at the right (not to scale). The
walk consists of four legs with the following magnitudes:
A = 46 m
B = 142 m
C = 78 m
D = 89 m
• Determine the magnitude and direction of Mia's resultant
displacement. Consider using a table to organize your
calculations.

74. objective
• Practice packet
• Go over homework
• Finish labs
• Vector practices packet

75. 10/28 do now
Vector quiz 2

76. Lesson 2: Projectile Motion
1. What is a Projectile?
2. Characteristics of a Projectile's Trajectory
3. Describing Projectiles with Numbers
a. Horizontal and Vertical Components of Velocity
b. Horizontal and Vertical Components of
Displacement
4. Initial Velocity Components
5. Horizontally Launched Projectiles - Problem-
Solving
6. Non-Horizontally Launched Projectiles -
Problem-Solving

77. objectives
1. What is a Projectile?
2. Characteristics of a Projectile's Trajectory
homework
1. Castle learning – projectile 1
2. Quarter ends 11/3 – next Thursday.
Please finish all your castle learning
assignment

78. What is a Projectile?
• A projectile is an object upon which the
only force acting is gravity.

80. Projectile Motion and Inertia
• Many people think that if an object is moving upward,
then there must be an upward force. And if an object is
moving upward and rightward, there must be both an
upward and rightward force. Their belief is that forces
cause motion;
• Such people do not believe in Newtonian physics: A
force is not required to keep an object in motion. A force
is only required to maintain an acceleration. If not acted
upon by an unbalanced force, "an object in motion will
stay in motion." This is Newton's law of inertia.

81. 10/31 do now

82. • With no gravity the cannon ball
would continue in motion in a
straight line at constant speed.
• What effect will gravity have
upon the motion of the
cannonball?
• Gravity will not affect the
cannonball's horizontal motion.
• Gravity will act downwards
upon the cannonball to affect
its vertical motion. Gravity
causes a vertical acceleration.
The ball will drop vertically
below its otherwise straight-
line, inertial path causes the
parabolic trajectory that is
characteristic of projectiles.

83. • Environment With No Gravity

84. • Environment with Gravity

85. • A projectile is an object upon which the only force is
gravity.
• Gravity acts to influence the vertical motion of the
projectile, thus causing a vertical acceleration.
• The horizontal motion of the projectile is the result of the
tendency of any object in motion to remain in motion at
constant velocity. Due to the absence of horizontal
forces, a projectile remains in motion with a constant
horizontal velocity.
• Horizontal forces are not required to keep a projectile
moving horizontally. The only force acting upon a
projectile is gravity!

86. Characteristics of a
Projectile's Trajectory
• There are the two components
of the projectile's motion -
horizontal and vertical motion.
These two perpendicular
components of motion are
independent of each other.

87. Horizontally Launched Projectiles
• A horizontally launched projectile is a projectile launched with
only horizontal speed. Its initial vertical speed is zero.
• Since the only force acting on the
projectile is gravity, which is in the
vertical downward direction, only
the vertical motion is affected.
Gravity causes a downward
acceleration. The cannonball falls
the same amount of distance as it
did when it was merely dropped
from rest.
• However, the vertical force acts
perpendicular to the horizontal
motion and will not affect the
horizontal motion since
perpendicular components of
motion are independent of each
other.
• Thus, the projectile travels
with a constant horizontal
velocity and a downward
vertical acceleration.

88. Horizontally Launched Projectile

89. • A non horizontally launched projectile is a projectile launched at an
angle with the horizontal. It has both initial horizontal and
vertical speed.
Non-Horizontally Launched Projectiles
• Since the only force acting on the
projectile is gravity, which is in the
vertical downward direction, only the
vertical motion is affected. Gravity
causes a downward acceleration. The
cannonball falls the same as it did when
it was merely tossed up with an initial
vertical speed.
• However, The vertical force acts
perpendicular to the horizontal motion
and will not affect the horizontal motion
since perpendicular components of
motion are independent of each other.
• Thus, the projectile travels with a constant horizontal velocity and a
downward vertical acceleration.

90. Non-Horizontally Launched Projectiles

91. Horizontal
Motion
Vertical
Motion
Forces
(Present? - Yes or No)
(If present, what dir'n?)
No
Yes
The force of gravity
acts downward
Acceleration
(Present? - Yes or No)
(If present, what dir'n?)
No
Yes
"g" is downward at
9.8 m/s/s
Velocity
(Constant or
Changing?)
Constant
Changing
(by 9.8 m/s each
second)
• Horizontal and vertical components are independent of each
other. Change of horizontal speed does not affect vertical
motion. Change of vertical speed does not affect horizontal
motion.

92. Check your understanding
• practice

93. What we know about projectile motion
• A projectile is any object upon which the only force is
gravity,
• Projectiles travel with a parabolic trajectory due to the
influence of gravity,
• There are no horizontal forces acting upon projectiles
and thus no horizontal acceleration,
• The horizontal velocity of a projectile is constant (a
never changing in value),
• There is a vertical acceleration caused by gravity; its
value is 9.81 m/s/s, down,
• The vertical velocity of a projectile changes by 9.81 m/s
each second,
• The horizontal motion of a projectile is independent of
its vertical motion.

94. Describing Projectiles with Numbers:
Horizontal and Vertical Components of
Velocity – horizontally launched projectile

95. Describing Projectiles with Numbers:
Horizontal and Vertical Components of
Velocity – horizontally launched projectile
• Horizontal motion is
constant: velocity is
constant.
• Vertical: same as drop
the ball from rest:
velocity is increasing by
9.81 m/s every second

96. Time
Horizontal
Velocity
Vertical
Velocity
0 s 20 m/s, right 0
1 s 20 m/s, right 9.8 m/s, down
2 s 20 m/s, right 19.6 m/s, down
3 s 20 m/s, right 29.4 m/s, down
4 s 20 m/s, right 39.2 m/s, down
5 s 20 m/s, right 49.0 m/s, down

97. Horizontal and Vertical Components of Velocity
• The horizontal velocity remains constant during the
course of the trajectory
• The vertical motion is the same as free fall from rest.
Its velocity increases by 9.81 m/s every second in
downward direction.
• There is a vertical force acting upon a projectile but
no horizontal force.
• A vertical force causes a vertical acceleration - in this
case, an acceleration of 9.81 m/s/s. There is no
horizontal acceleration.

98. Describing Projectiles with Numbers:
Horizontal and Vertical Components of
Velocity – projectile launched at an angle

99. Describing Projectiles with Numbers:
Horizontal and Vertical Components of
Velocity – projectile launched at an angle
• Horizontal motion is constant:
velocity is constant.
• Vertical: same as free fall
with initial upward velocity:
velocity is decreasing as it
goes up, reaches zero and
increasing as it comes
down.

100. Time
Horizontal
Velocity
Vertical
Velocity
0 s 73.1 m/s, right 19.6 m/s, up
1 s 73.1 m/s, right 9.8 m/s, up
2 s 73.1 m/s, right 0 m/s
3 s 73.1 m/s, right 9.8 m/s, down
4 s 73.1 m/s, right 19.6 m/s, down
5 s 73.1 m/s, right 29.4 m/s, down
6 s 73.1 m/s, right 39.2 m/s, down
7 s 73.1 m/s, right 49.0 m/s, down

101. Horizontal and Vertical Components of Velocity
• The horizontal velocity remains constant during the course of
the trajectory
• The vertical velocity changes by 9.81 m/s every second.
– As the projectile rises towards its peak, it is slowing down
(0 m/s at the very top); and as it falls from its peak, it is
speeding up.
– the projectile's motion is symmetrical: the magnitude of the
vertical velocity (i.e., vertical speed) is the same an equal
interval of time on either side of its peak. At the peak itself,
the vertical velocity is 0 m/s; the velocity vector is entirely
horizontal at this point in the trajectory.
• There is a vertical force acting upon a projectile but no
horizontal force.
• A vertical force causes a vertical acceleration - in this case, an
acceleration of 9.81 m/s/s. There is no horizontal
acceleration.

102. The symmetrical nature of a non-horizontally launched
projectile that lands at the same height as which it is
launched.

103. Describing Projectiles With Numbers:
(Horizontal and Vertical Displacement) -
horizontally launched projectiles
• Horizontal motion is
constant: x = vix∙t
• Vertical: same as free fall
with initial zero velocity:
y = ½ a∙t2
(a = - 9.81 m/s2
)

104. Time
Horizontal
Displacement
Vertical
Displacement
0 s 0 m 0 m
1 s 20 m -4.9 m
2 s 40 m -19.6 m
3 s 60 m -44.1 m
4 s 80m -78.4 m
5 s 100 m -122.5 m
• The vertical distance fallen from rest during each
consecutive second is increasing (i.e., there is a vertical
acceleration).
• The horizontal distance traveled by the projectile each
second is a constant value.

105. Describing Projectiles With Numbers:
(Horizontal and Vertical Displacement)
- projectiles launched at an angle
• Horizontal motion is constant:
x = vix∙t
• Vertical: same as free fall
with initial upward velocity:
y = viyt - ½∙a∙t2
(a
= -9.81 m/s2
)

106. Time
Horizontal
Displacement
Vertical
Displacement
0 s 0 m 0 m
1 s 33.9 m 14.7 m
2 s 67.8 m 19.6 m
3 s 101.7 m 14.7 m
4 s 135.6 m 0 m
• The symmetrical nature of a projectile's trajectory: the
vertical displacement of a projectile t seconds before
reaching the peak is the same as the vertical
displacement of a projectile t seconds after reaching the
peak.
• The horizontal distance traveled by the projectile each
second is a constant value.

107. Check your understanding

108. Initial Velocity Components
• The horizontal and vertical motions of a projectile are
independent of each other. The horizontal velocity of a
projectile does not affect how far (or how fast) a
projectile falls vertically.
• Be careful not to mix horizontal motion information with
vertical motion information.
• Only vertical motion parameters (initial vertical velocity,
final vertical velocity, vertical acceleration) determine the
vertical displacement.
• Only horizontal motion parameters (initial horizontal
velocity, final horizontal velocity, horizontal acceleration).
Determine the horizontal displacement.
• One of the initial steps of a projectile motion problem is
to determine the components of the initial velocity.

109. • Since velocity is a vector quantity, vector
resolution is used to determine the
components of velocity.
θ
vi
vix
viy
SOH CAH TOA
sinθ = viy / vi
viy = visinθ
cosθ = vix / vi
vix = vicosθ
• Special case: horizontally launched projectile:
• θ = 0o
: viy = visinθ = 0; vix = vicosθ = vi

110. • Practice A: A water balloon is launched
with a speed of 40 m/s at an angle of 60
degrees to the horizontal.

111. • Practice B: A motorcycle stunt person
traveling 70 mi/hr jumps off a ramp at an
angle of 35 degrees to the horizontal.

112. • Practice C: A springboard diver jumps
with a velocity of 10 m/s at an angle of
80 degrees to the horizontal.

113. • The point of resolving an initial velocity
vector into its two components is to use
the values of these two components to
analyze a projectile's motion and
determine such parameters as
– the horizontal displacement,
– the vertical displacement,
– the final vertical velocity,
– the time to reach the peak of the trajectory,
– the time to fall to the ground, etc.

114. Determination of the Time of Flight for
projectile launched at an angle, given
initial speed and angle:
For the given projectile, we can determine the initial
horizontal and vertical velocity: viy = visinθ; vix = vicosθ
For a projectile launched at an angle, its vertical motion is
the same as free fall with initial vertical velocity:
• At the very top, vy = 0
• vy = viy + at
• 0 = viy – g∙tup (a = -g)
tup = viy / g
If we know the initial vertical velocity, we can
determine the time to reach the highest the point
and the total time of flight.
ttotal = 2 tup = 2viy / g

115. Determination of Horizontal
Displacement for projectile launched at
an angle, given initial speed and angle
and time of flight
For the given projectile, we can determine the initial
horizontal and vertical velocity: viy = visinθ; vix = vicosθ
For a projectile launched at an angle, its horizontal motion
is constant. To determine its horizontal displacement we
can use
x = vix∙t

116. Determination of Determination of the
Peak Height for projectile launched at an
angle, given initial speed and angle
For the given projectile, we can determine the initial
horizontal and vertical velocity: viy = visinθ; vix = vicosθ
For a projectile launched at an angle, its vertical motion is
the same as free fall with initial vertical velocity:
• At the very top, vy = 0
• vy
2
= viy
2
+ 2a∙y
• 0 = viy
2
– 2g∙ypeak (a = -g)
ypeak = viy
2
/ 2g

117. Check your understanding

118. Horizontally Launched
Projectile Problems
• A projectile is launched with an initial horizontal velocity from an
elevated position and follows a parabolic path to the ground.
Predictable unknowns include the initial speed of the projectile, the
initial height of the projectile, the time of flight, and the horizontal
distance of the projectile.
Example:
• A pool ball leaves a 0.60-meter high table with an initial horizontal
velocity of 2.4 m/s. Predict the time required for the pool ball to fall to
the ground and the horizontal distance between the table's edge and
the ball's landing location.
• A soccer ball is kicked horizontally off a 22.0-meter high hill and lands
a distance of 35.0 meters from the edge of the hill. Determine the
initial horizontal velocity of the soccer ball.

119. • Three common kinematics equations that
will be used for solving projectile
problems:

120. Horizontal
motion
Vertical
motion

121. Example
• A pool ball leaves a 0.60-meter high table with an initial
horizontal velocity of 2.4 m/s. Predict the time required for the
pool ball to fall to the ground and the horizontal distance
between the table's edge and the ball's landing location.
Horizontal
Information
Vertical
Information
vix
= 2.4 m/s
ax
= 0 m/s/s
x = ?
y = -0.60 m
viy
= 0 m/s
ay
= -9.8 m/s/s
• It will almost always be the case that one of the vertical
equations be used to determine the time of flight of the
projectile and then one of the horizontal equations be
used to find the other unknown quantities (or vice versa -
first use the horizontal and then the vertical equation).

122. y = viy
•t + ½ •ay
•t2
• Solve for t – use vertical information:
-0.60 m = (0 m/s)•t + ½ •(-9.8 m/s/s)•t2
-0.60 m = (-4.9 m/s/s)•t2
0.122 s2
= t2
t = 0.350 s
• Solve for x – use horizontal information:
x = vix
•t + ½ •ax
•t2
x = (2.4 m/s)•(0.3499 s) + 0.5•(0 m/s/s)•(0.3499 s)2
x = (2.4 m/s)•(0.3499 s)
x = 0.84 m

123. practice
• A soccer ball is kicked horizontally off a 22.0-meter high
hill and lands a distance of 35.0 meters from the edge of
the hill. Determine the initial horizontal velocity of the
soccer ball.
Horizontal Information Vertical Information
x = 35.0 m
ax
= 0 m/s/s
vix
= ?
y = -22.0 m
viy
= 0 m/s
ay
= -9.8 m/s/s

124. y = viy
•t + ½ •ay
•t2
• Solve for t – use vertical information:
-22.0 m = (0 m/s)•t + ½ •(-9.8 m/s/s)•t2
-22.0 m = (-4.9 m/s/s)•t2
t = 2.12 s
• Solve for vix – use horizontal information:
x = vix
•t + ½ •ax
•t2
35 m = vix•(2.12 s) + 0.5•(0 m/s/s)•(2.12 s)2
35 m = vix•(2.12 s)
vix = 16.5 m/s

125. Non-Horizontally Launched
Projectile Problems
• A projectile is launched at an angle to the horizontal and
rises upwards to a peak while moving horizontally. Upon
reaching the peak, the projectile falls with a motion that is
symmetrical to its path upwards to the peak. Predictable
unknowns include the time of flight, the horizontal range,
and the height of the projectile when it is at its peak.
Examples:
• A football is kicked with an initial velocity of 25 m/s at an
angle of 45-degrees with the horizontal. Determine the time
of flight, the horizontal distance, and the peak height of the
football.

126. Horizontal
motion
Vertical
motion

127. Example
• A football is kicked with an initial velocity of 25 m/s at an
angle of 45-degrees with the horizontal. Determine the
time of flight, the horizontal displacement, and the peak
height of the football.
Horizontal Component Vertical Component
vix
= vi
•cosθ
vix
= 25 m/s•cos45o
vix
= 17.7 m/s
vfx
= 17.7 m/s
ax
= 0 m/s/s
x = ?
viy
= vi
•sinθ
viy
= 25 m/s•sin45o
viy
= 17.7 m/s
vfy
= -17.7 m/s
ay
= -9.8 m/s/s
y = ?
• Due to the symmetrical nature of a projectile's
trajectory: viy = - vfy

128. • Solve for t – use vertical information:
t = 3.61 s
• Solve for x – use horizontal information:
x = vix
•t + ½ •ax
•t2
x = 63.8 m
ttotal = 2 tup = 2viy / g
• Solve for peak height – use vertical information:
ypeak = viy
2
/ 2g
ypeak = 15.9 m

129. example
• A long jumper leaves the ground with an initial velocity of
12 m/s at an angle of 28-degrees above the horizontal.
Determine the time of flight, the horizontal distance, and
the peak height of the long-jumper.
Horizontal Component Vertical Component
vix
= vi
•cosθ
vix
= 12 m/s•cos28o
vix
= 10.6 m/s
vfx
= 10.6 m/s
ax
= 0 m/s/s
x = ?
viy
= vi
•sinθ
viy
= 12 m/s•sin28o
viy
= 5.6 m/s
vfy
= -5.6 m/s
ay
= -9.8 m/s/s
y = ?
t = 1.1 s x = 12.2 m ypeak = 1.6 m

130. practice

131. Lesson 3 : Forces in Two
Dimensions
1. Addition of Forces
2. Resolution of Forces
3. Equilibrium and Static
4. Net Force Problems Revisited
5. Inclined Planes

132. Addition of Forces
• Newton’s 2nd
Law: ∑F = ma (∑F is the net force)

133. • When forces acting at angles to the
horizontal, Newton’s 2nd
law still
applies:
• Force is a vector quantity. Adding
forces in 2 dimensions follows the
rules for adding vectors.
∑F = ma
• The two ways for adding vectors are:
1. Head and tail method
2. Mathematical method: Using vector resolution and
Pythagorean Theorem to determine magnitude and
tangent function to determine direction

134. Head and tail method
• The net force (vector sum of
all the forces) is 0 Newton.
The object is at rest and
staying at rest. The object is
at equilibrium. Any object
upon which all the forces are
balanced (Fnet = 0 N) is said to
be at equilibrium.

135. Example: determine the net force

136. The principles of adding forces:
10 Newton + 10 Newton = ?

137. • The resultant of any two vectors A and B is
greatest when the angle between them is zero
degrees. It decreases as the angle between the
vectors increases. It is smallest when the angle
between the two vectors is 180 degrees.
• The resultant can be any value between
maximum (A+B) and minimum |A-B|

138. example
• A force of 6.0 Newton north and a force of
8.0 Newton east act concurrently on an
object. The magnitude of the resultant of the
two forces can not be
1. 1.3 N
2. 2.0 N
3. 10. N
4. 14 N

139. example
A 3.0-newton force and a 4.0-newton force
act concurrently on a point. In which
diagram below would the orientation of
these forces produce the greatest net
force on the point?
C
D
A
B

140. example
• Which pair of concurrent forces could
produce a resultant force having a magnitude
of 10. Newton?
1. 10. N, 10. N
2. 10. N, 30. N
3. 4.7 N, 4.7 N
4. 4.7 N, 50. N

141. • Which pair of forces acting concurrently on
an object will produce the resultant of
greatest magnitude?
1. 2. 3. 4.
A B C D

142. Check your understanding

143. Resolution of Forces
• Any vector that is directed at an angle to the customary
coordinate axis can be considered to have two parts -
each part being directed along one of the axes - either
horizontally or vertically.
• The parts of the single vector are called components
and describe the influence of that single vector in that
given direction.

146. practice

147. An important concept
• The force is the same magnitude in each
diagram; only the angle with the horizontal
is changing. As the angle that a force
makes with the horizontal increases,
the component of force in the
horizontal direction (Fx) decreases. The
more that a force is directed upwards (the
angle with the horizontal increases), the
less that the force is able to exert an
influence in the horizontal direction.

148. Force resolution and sail boating
• Sailboats encounter a force of wind against the sail. This
force is directed perpendicular to the face of the sail. The
actual direction of this force is dependent upon the
orientation of the sail.
• To determine the influence of the wind resistance force
in the direction of motion, that force is resolved into two
components - one in the direction that the sailboat is
moving and the other in a direction perpendicular to the
sailboat's motion.

149. • Many people believe that a sailboat cannot travel
"upwind." This is simply not true. Sailboats can travel
"upwind" and commonly do so by a method known as
tacking into the wind.

150. Equilibrium and Statics
• When all the forces that act upon an object are
balanced, then the object is said to be in a state of
equilibrium.
• An object at equilibrium is either ...
• at rest and staying at rest, or
• in motion and continuing in motion with the same speed
and direction.

151. • If an object is at rest and is in a state of
equilibrium, then we would say that the
object is at "static equilibrium."
• "Static" means stationary or at rest.
• If the object is at equilibrium, then the net
force acting upon the object should be 0
Newton. The resultant force (the vector
sum) is 0 Newton.

152. example
• Forces A, B, C acting on a point. Determine if
they produce equilibrium on the point.
Force A Force B Force C
Magnitude 3.4 N 9.2 N 9.8 N
Direction 161 deg. 70 deg. 270 deg

153. Head and tail method to determine
resultant

154. • Another way of determining the net force (vector sum of all the
forces) involves using the trigonometric functions to resolve
each force into its horizontal and vertical components. Once
the components are known, they can be compared to see if
the vertical forces are balanced and if the horizontal forces are
balanced.
• The data in the
table above
show that the
forces nearly
balance. We
could say it's
"close enough."

155. • The analysis of the forces acting upon an object in
equilibrium is commonly used to analyze situations
involving objects at static equilibrium.
• Example: a frame is shown with the given tension.
Determine the weight of the frame.
(50N)cos30 = 43 N(50N)cos120 = -43 N
(50N)sin30 + (50N)sin30 = 50 N
Fg = 50 N

156. example
• A sign is shown with the given mass of 5 kg.
Determine the tension of each cable.
Fg = mg = 49 N
TT
-Tcos40o
40o
40o
Tcos40o
Tsin40o
+ Tsin40o
Tsin40o
+ Tsin40o
= 49 N
2Tsin40o
= 49 N
T = 38.1 N

157. an important principle
• As the angle with the horizontal increases, the amount of
tensional force required to hold the sign at equilibrium
decreases.
Fg = 10 N

158. • In conclusion, equilibrium is the state of an object in
which all the forces acting upon it are balanced. In such
cases, the net force is 0 Newton. Knowing the forces
acting upon an object, trigonometric functions can be
utilized to determine the horizontal and vertical
components of each force. If at equilibrium, then all the
vertical components must balance and all the horizontal
components must balance.

159. Check your understanding

160. Net Force Problems Revisited
• A force directed an angle can be resolved into
two components - a horizontal and a vertical
component.
• The acceleration of an object is related to the
net force acting upon the object and the mass of
the object (Newton's second law).
• We will determine the net force when force
vectors directed at angles and use Newton’s 2nd
law to solve problems.

161. example
• The vertical forces are balanced (Fgrav
, Fy
, and Fnorm
add up to 0 N),
• The horizontal forces add up to 29.3 N, right
• The net force is 29.3 N, right
• a = Fnet / m = 29.3 N / 10 kg = 2.93 m/s2
, right

162. Determine the net force and
acceleration
• Fnet = 69.9 N, right
• m = (Fgrav / g) = 20 kg
• a = (69.9 N) / (20 kg) =3.50 m/s/s, right

163. Determine the net force and
acceleration
• Fnet = 30.7 N, right
• a = 1.23 m/s/s, right.

164. practice

165. Procedures for adding vectors at an
angle with horizontal
1. Resolve the vectors at an angle into x
and y components.
2. Add all the x components together
3. Add all the y components together
4. Use Pythagorean Theorem to find the
resultant (hypotenuse)
5. Resultant2
= x2
+ y2
6. Use trigonometric function to determine
the direction: tanθ = opp / adj

166. example
• Find resultant force and
acceleration if
– F = 10 N;
– θ = 30o
– mg = 20 N
– Fn = 15 N
F Fnmg
+ +
• Fx = Fcosθ = (10N)cos30o
= 8.67 N
• Fx = Fsinθ = (10N)sin30o
= 5.00 N
Fnet = 8.67 N, up
a = Fnet/m = 4.34 m/s2
, up

167. F 20 N
+ +=
Fnmg
+ +
Fx = 8.67 N
+
15 N
Fy = 5 N
Fx = 8.67 N
R
Fnet = 8.67 N
θ = 0o

168. Practice: Find the resultant force Fnet and a
• given: Fn = 10. N; Fapp = 20. N; Fg = 20. N; Ff = 17 N
Fapp
Fg (weight)
Fn (Normal force)
Ff (frictional force)
30.o
Fnet = 0.0 N
a = 0
Fappx = 17 N
Fappy = 10 N
Fn
Ff
Fg
Fapp
R = 0.0 N
• Head and tail method
• Mathematical method

169. determine the net force and
acceleration

170. Head and tail method

171. Resolving vectors at an angle, using Pythagorean
theorem to determine the magnitude and tangent
function to determine direction
=
21 N
21 N
-14 N
-14 N
∑Fx = 32 N
∑Fy = -23 N
Fnet
2
= (∑Fx)2
+ (∑Fy)2
Fnet = 39 N
θ = tan-1
(-23/32) = -36o
θ = 324o
CCW
a = Fnet / m = 39 N / 5 kg = 8.0 m/s2
, same
direction as the force

172. Check your understanding

173. Inclined Planes
• Objects accelerate down inclined planes because of an
unbalanced force.
• Note: the normal force is not directed
in the direction that we are
accustomed to. The normal forces are
always directed perpendicular to the
surface that the object is on.

174. An important idea
• The process of analyzing the forces acting upon objects
on inclined planes will involve resolving the weight vector
(Fgrav
) into two perpendicular components.
• The perpendicular component of the force of gravity is
directed opposite the normal force and as such balances the
normal force.
• The parallel component of the force of gravity is not balanced
by any other force. This object will accelerate down the
inclined plane due to this unbalanced force.

175. • In the absence of friction
• Fnet = F//
• mgsinθ = ma
• a = gsinθ

176. • In the presence of friction or other forces
(applied force, tensional forces, etc.), the
situation is slightly more complicated.
• The net force is the vector sum of all the
forces.
– All the perpendicular components (including
the normal force) add to 0 N.
– All the parallel components (including the
friction force) add together to yield the net
force. Which should directed along the
incline.

177. • The net force = 5 N down
the inline.
• Incline problems can be
simplified through a useful
trick known as "tilting the
head."

178. example
• The free-body diagram shows the forces acting upon a 100-
kg crate that is sliding down an inclined plane. The plane is
inclined at an angle of 30 degrees. The coefficient of friction
between the crate and the incline is 0.3. Determine the net
force and acceleration of the crate.
Fnorm = F┴ = Fgrav∙cos30o
Fnorm = 850 N
Fnet = F// - Ff
Fnet = Fgrav∙sin30o
- µFnorm
Fnet = 235 N
a = Fnet / m = 2.35 m/s2

179. practice

180. Check your understanding

181. • Vectors – Lab - How do the N-S, E-W
legs of a trip compare to the overall
displacement of that trip?

182. Lab 7 – determine displacement
• Question:
How do the N-S, E-W legs of a trip compare to the overall
displacement of that trip?
Purpose:
To identify the mathematical relationship between the N-S and E-W
legs of a trip to the overall displacement for that trip.
A complete lab write-up includes a Title, a Purpose, a Data section,
and a Conclusion/Discussion. The Data section should include the
provided table with the required trips and one self-designed trip. The
Conclusion/Discussion should identify the mathematical relationship
between the legs of the trip and the overall displacement for that
trip; the relationship should be general enough to be applied to any
trip in order to determine the overall displacement from a statement
of the legs. Two of the four trips (at least one of which is a three-
legged trip) should be mathematically analyzed to provide the
supporting evidence for your conclusion; work should be shown,
labeled and discussed in an organized fashion.

183. Lab 7 – determine displacement
Purpose:
To identify the mathematical relationship between the N-S and E-W legs of a trip to the
overall displacement for that trip.
Materieal: measuring tapes, protractors
Data:
Conclusion: identify the mathematical relationship between the legs of the trip and the
overall displacement for that trip; the relationship should be general enough to be
applied to any trip in order to determine the overall displacement from a statement of
the legs. Two of the four trips should be mathematically analyzed (at least one of
which is a three-legged trip) to provide the supporting evidence for your conclusion;
work should be shown, labeled and discussed in an organized fashion.
A complete lab write-up includes a Title, a Purpose, a Data section, and a
Conclusion/Discussion.
North
(m)
East
(m)
South
(m )
west
(m)
Disp. (m) Direction with east (o
)
4 3
6 4 3
6 8 2 5
7 7 4 3

184. Lab 8 – measuring heights using trigonometry
• Purpose(5 points): To determine the heights of objects using
trigonometry.
• Material(5 points): protractor, straw, tapes, metersticks.
• Objects to be measured: LCD projector (in class prctice),
Scoreboard, announcer box on top of bleachers, footbal field
ligth fixtrue, highschool roof

185. Procedure
• Construct a sight protractor like the one in the image below by attaching a
straw to the straight edge of the protractor and hanging a weight from the
center.
• By looking at the top of an object through this straw, you will be able to
measure an angle of inclination leading to the top of the object. You can
also measure the distance from the point of angle measurement to the
object. Using trigonometry, the angle and the distance from the object
should be enough to calculate the height of the object. Don’t forget—you
are measuring the height from your eye, so you must add the height of your
eye to the calculated height of the object!

186. Data and Calculations:
LCD Projector
Angle measured ________
Distance from object _______
Height of eye _______
Height of projector _______
Scoreboard
Angle measured ________
Distance from object _______
Height of eye _______
Height of scoreboard _______
Bleachers (top of announcer’s
booth)
Angle measured ________
Distance from object _______
Height of eye _______
Height of bleachers _______
Lights
Angle measured ________
Distance from object _______
Height of eye _______
Height of lights _______
Batting Cage
Angle measured ________
Distance from object _______
Height of eye _______
Height of batting cage _______
Gym Roof
Angle measured ________
Distance from object _______
Height of eye _______
Height of gym roof _______
Show one sample of picture and calculation

187. Conclusion (20 points)
Procedure (10 points):
– Briefly describe how the lab is going to be done. Someone
who was not present during the lab should be able to
understand how the experiment was perforem and be able to
reporduce the results by reading your procedure.
The Discussion of results (10 points)
– Discuss any questionable data or surprising result. An error
analysis should be included. Suggest any change in
experimental design which might test your explanations
A complete lab write-up includes Title, Purpose,
Material, Data section, and Conclusion.