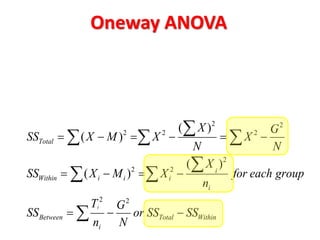
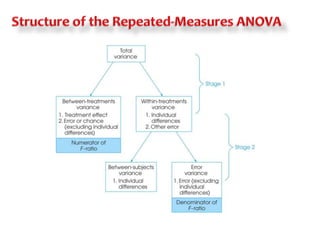
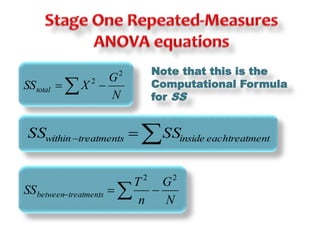
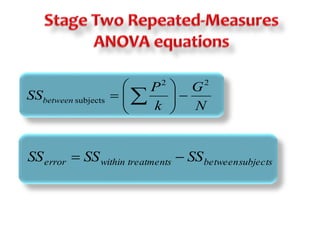
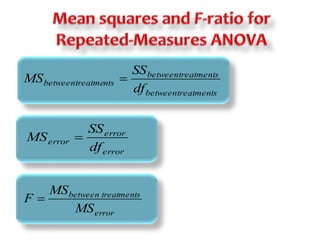
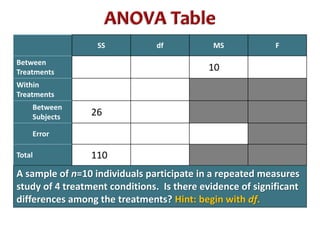
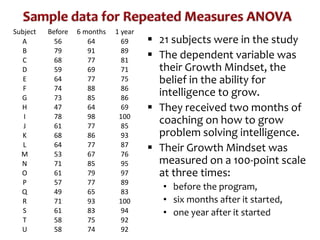
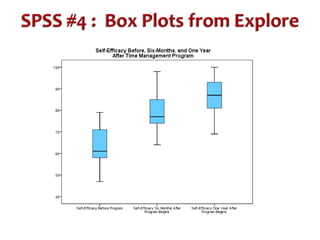
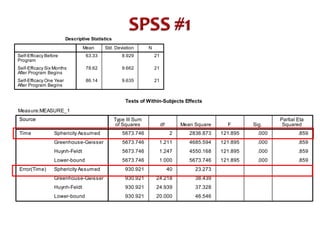
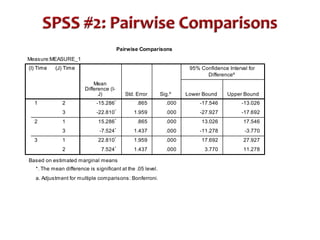
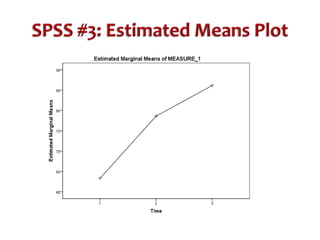
This document discusses repeated measures analysis of variance (ANOVA). It explains that repeated measures ANOVA compares measures taken on the same subjects across different treatment conditions, controlling for individual differences. It provides the computational formulas for calculating sums of squares for between treatments, between subjects, and error. It also discusses degrees of freedom, mean squares, and the F-ratio test used to determine if there are significant differences among treatment means while accounting for correlations between measures from the same subject.

2.  Independent-measures analysis of
variance (Oneway ANOVA)
 Repeated measures designs (t-tests)
 Individual differences

3. Oneway ANOVA
     
X
X
   
Total Within
i
Total
Between
i
i
Within i i i
or SS SS
G
N
T
n
SS
G
for each group
n
SS X M X
N
X
N
SS X M X
i

  

 


 
2 2
2
2 2
2
2
2
2 2
( )
( )
( )
( )

4.  Independent Samples
 Compare two groups
that are unrelated to
each other
 Numerator is
difference between
groups
 Does not control for
the impact of
individual differences
 Related Samples
 Compare two
measures from one
person or one related
pair of people
 Numerator is
difference within pair
 Controls for the impact
of individual
differences

5.  Null hypothesis: in the population, there are no
mean differences among the treatment groups
: ... 0 1 2 3 H   
 Alternate hypothesis states that there are
mean differences among the treatment groups.
H1: At least one treatment mean μ
is different from another

6.  F ratio based on variances
variance (differences) between treatments
variance (differences) expected with no treatment effect,
(individual differences removed)
F 
• Same structure as independent measures
• Variance due to individual differences is
not present

7.  Participant characteristics that vary from
one person to another.
• Not systematically present in any treatment
group or by research design
 Characteristics may influence
measurements on the outcome variable
• Eliminated from the numerator by the
research design
• Must be removed from the denominator
statistically

8.  Numerator of the F ratio includes
• Systematic differences caused by treatments
• Unsystematic differences caused by random
factors (reduced because same individuals in
all treatments)
 Denominator estimates variance
reasonable to expect from unsystematic
factors
• Effect of individual differences is removed
• Residual (error) variance remains

9. Repeated Measures ANOVA
Total Variability
Between
Treatments
Within
Treatments
Between
Subjects
Error
Variance

11.  (Equations follow)
 First stage
• Identical to independent samples ANOVA
• Compute SSTotal =
SSBetween treatments + SSWithin treatments
 Second stage
• Removing the individual differences from the
denominator
• Compute SSBetween subjects and subtract it from
SSWithin treatments to find SSError

12.  There is a computational equation for the Sum
of Squared Deviations from the Mean:
2 ( X
)
N
 X

2
 With ANOVA, we sum groups of means
• G2 = Sum of all the scores squared
• T1 = sum of scores in Treatment Group 1
• P1 = sum of scores of Person 1 across time
• TA 1 and TB 1 = sums of scores across levels of a factor.

13. G
N
SS X total
2
2  
Note that this is the
Computational Formula
for SS
 withintreatments inside each treatment SS SS
G
N
T
n
SS between treatments
2 2
  

14. G
N
P
k
SSbetween
2 2


 
subjects   

 

error within treatments between subjects SS  SS  SS

15. dftotal = N – 1
dfwithin treatments = Σdfinside each treatment
dfbetween treatments = k – 1
dfbetween subjects = n – 1
dferror = dfwithin treatments – dfbetween subjects

16. MS 
error
SS
error
MS 
error df
between treatments
SS
between treatments
between treatments df
between treatments
MS
error
MS
F 

18.  Find your partners
 Solve the ANOVA
table problem
 Try to finish in 10
minutes (1 minute
per slot to complete)

19. SS df MS F
Between
Treatments 10
Within
Treatments
Between
Subjects 26
Error
Total 110
A sample of n=10 individuals participate in a repeated measures
study of 4 treatment conditions. Is there evidence of significant
differences among the treatments? Hint: begin with df.

21. Subject Before 6 months 1 year
A 56 64 69
B 79 91 89
C 68 77 81
D 59 69 71
E 64 77 75
F 74 88 86
G 73 85 86
H 47 64 69
I 78 98 100
J 61 77 85
K 68 86 93
L 64 77 87
M 53 67 76
N 71 85 95
O 61 79 97
P 57 77 89
Q 49 65 83
R 71 93 100
S 61 83 94
T 58 75 92
U 58 74 92
 21 subjects were in the study
 The dependent variable was
their Growth Mindset, the
belief in the ability for
intelligence to grow.
 They received two months of
coaching on how to grow
problem solving intelligence.
 Their Growth Mindset was
measured on a 100-point scale
at three times:
• before the program,
• six months after it started,
• one year after it started

22.  Much more output than you want
 Need to ask for some Options to get SPSS to do
as much of the work as possible.
• Descriptives
• Plots
• Multiple Comparisons
• Effect Size

23.  Analyze
  Descriptives
  Explore
 Follow steps on
diagram at right

29.  Percentage of variance explained by the
treatment differences
 Partial η2 is percentage of variability that has
not already been explained by other factors
between treatments
error
between treatments
SS
total between subjects
SS
SS
SS SS


 2 

30.  Determine exactly where significant
differences exist among more than two
treatment means
• Tukey’s HSD can be used (almost always
same number of subjects) or Scheffé if
dropouts mean unequal measures.
• Substitute SSerror and dferror in the formulas

31. Can people increase their actual problem-solving intelligence by
learning that their brains are able to change? Researchers found
the Growth Mindset of 21 people increased from just before they
began a Growth Mindset Coaching Program (M=63.3, s=8.9),
when measured six months (M=78.6, s=9.6) and one year after
starting the program (M=86.1, s=9.6). The differences were
significant (F(2,40)=121.89, p<.001). Post-hoc tests with
Bonferroni correction showed that self-efficacy at each time was
significantly improved from the one before. In fact, the impact of
the training program was large, with about 86% of the variability
in Problem Solving Growth Mindset related to the training
(2=.859). The coaching program seems to be an effective way
to help people tap into the potential of the Growth Mindset.

32.  The observations within each treatment
condition must be independent.
 The population distribution within each
treatment must be normal.
 The variances of the population
distribution for each treatment should be
equivalent.

33.  Decide if each of the following statements
is True or False.
• For the repeated-measures ANOVA,
degrees of freedom for SSerror is
(N–k) – (n–1).
T/F

34. • N is the number of scores and n
is the number of participants False