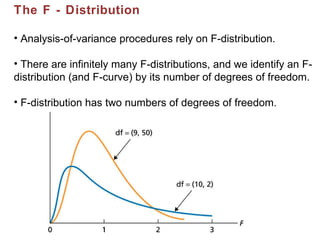
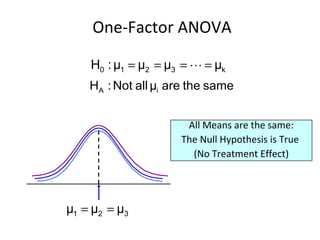
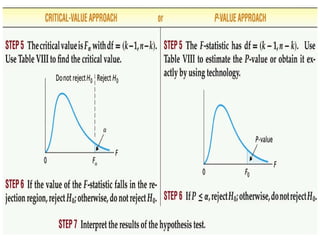
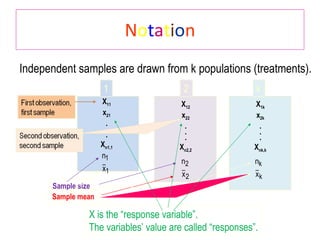
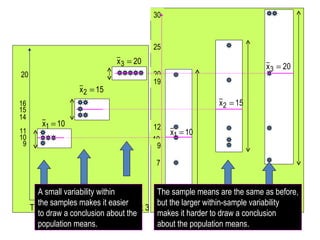
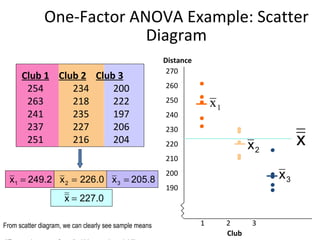
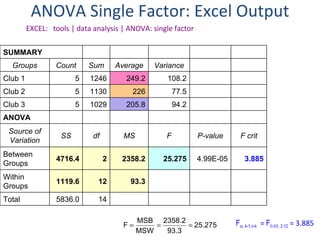
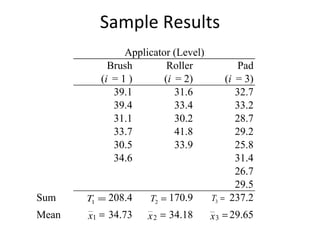
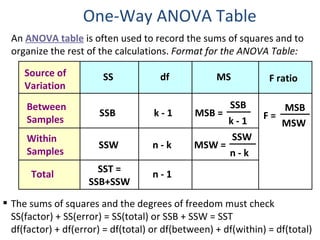
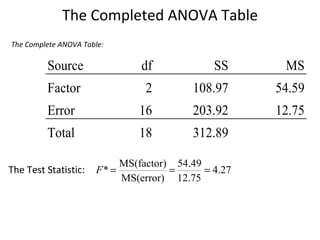
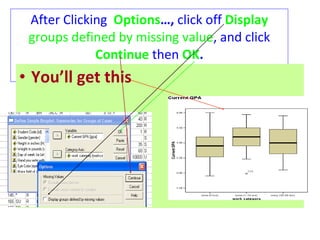
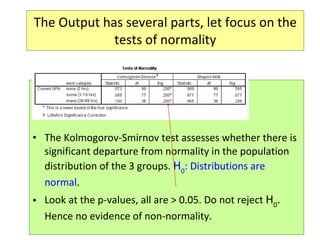
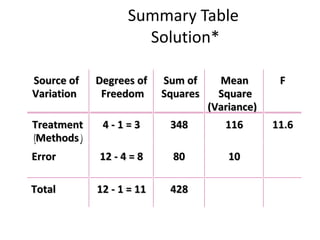
This document provides information on performing a one-way analysis of variance (ANOVA). It discusses the F-distribution, key terms used in ANOVA like factors and treatments, and how to calculate and interpret an ANOVA test statistic. An example demonstrates how to conduct a one-way ANOVA to determine if three golf clubs produce different average driving distances.

1. Hazilah Mohd Amin Analysis of Variance (ANOVA)

4. Key Fact F distribuition curve:

6. Table 12.1 (p. 534) Critical value: F  , 8,14 = 2.70

8. One-Factor ANOVA All Means are the same: The Null Hypothesis is True (No Treatment Effect)

9. One-Factor ANOVA At least one mean is different: The Null Hypothesis is NOT true (Treatment Effect is present) or

10. One-Way Analysis of Variance

16. N o t a t i o n Independent samples are drawn from k populations (treatments). X 11 x 21 . . . X n1,1 X 12 x 22 . . . X n2,2 X 1k x 2k . . . X nk,k Sample size Sample mean X is the “response variable”. The variables’ value are called “responses”.

19. One Way A n a l y s i s o f V a r i a n c e Graphical demonstration : Employing two types of variability: Within Samples and Between Samples

20. Treatment 1 Treatment 2 Treatment 3 20 16 15 14 11 10 9 The sample means are the same as before, but the larger within-sample variability makes it harder to draw a conclusion about the population means. A small variability within the samples makes it easier to draw a conclusion about the population means. 20 25 30 1 7 Treatment 1 Treatment 2 Treatment 3 10 12 19 9

21. One-Factor ANOVA Example: Scatter Diagram • • • • • 270 260 250 240 230 220 210 200 190 • • • • • • • • • • Distance Club 1 Club 2 Club 3 254 234 200 263 218 222 241 235 197 237 227 206 251 216 204 Club 1 2 3 From scatter diagram, we can clearly see sample means difference because of small within-sample variability

23. One-Factor ANOVA Example Computations Club 1 Club 2 Club 3 254 234 200 263 218 222 241 235 197 237 227 206 251 216 204 x 1 = 249.2 x 2 = 226.0 x 3 = 205.8 x = 227.0 n 1 = 5 n 2 = 5 n 3 = 5 n = 15 k = 3 MSB = 4716.4 / (3-1) = 2358.2 MSW = 1119.6 / (15-3) = 93.3 SSB = 4716.4 SSW = 1119.6

25. ANOVA Single Factor: Excel Output EXCEL: tools | data analysis | ANOVA: single factor F  , k-1,n-k = F  , 2,12 = 3.885 SUMMARY Groups Count Sum Average Variance Club 1 5 1246 249.2 108.2 Club 2 5 1130 226 77.5 Club 3 5 1029 205.8 94.2 ANOVA Source of Variation SS df MS F P-value F crit Between Groups 4716.4 2 2358.2 25.275 4.99E-05 3.885 Within Groups 1119.6 12 93.3 Total 5836.0 14

30. Notation Used in ANOVA Factor Levels Sample from Sample from Sample from Sample from Replication Level 1 Level 2 Level 3 Level k n = 1 x 1,1 x 2,1 x 3,1 x k ,1 n = 2 x 1,2 x 2,2 x 3,2 x k ,2 n = 3 x 1,3 x 2,3 x 3,3 x k ,3 Column T 1 T 2 T 3 T k T Totals T = grand total = sum of all x 's =  x =  T i . . . . . . . . .

31. Sample Results  1 x  2 x  3 x

36. Variation Sums of Squares

37. Mean Square The mean square for the factor being tested and for the error is obtained by dividing the sum-of-square value by the corresponding number of degrees of freedom Numerator degrees of freedom = df(factor) = k  1 = 3  1 = 2 df(total) = n  1 = 19  1 = 18 Denominator degrees of freedom = df(error) = n  k = 19  3 = 16 Calculations:

39. The Completed ANOVA Table The Complete ANOVA Table: The Test Statistic:

40. Solution Continued The Results a. Decision: Reject H o at  = 0.05 b. Conclusion : There is evidence to suggest the three population means are not all the same. The type of applicator has a significant effect on the paint drying time at the 0.05 level of significance. Critical Value: F  , k-1,n-k = F  , 2,16 = 3.63 The Test Statistic F = 4.27 is in the rejection region. Reject H 0 F .05 = 3.63 Do not reject H 0  = .05

42. Hey! Lets get our hand dirty … Using S P S S ….

53. End of ANOVA See U Later…

55. Summary Table Solution* Source of Variation Degrees of Freedom Sum of Squares Mean Square (Variance) F Treatment ( Methods ) 4 - 1 = 3 348 116 11.6 Error 12 - 4 = 8 80 10 Total 12 - 1 = 11 428