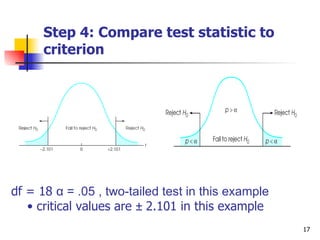
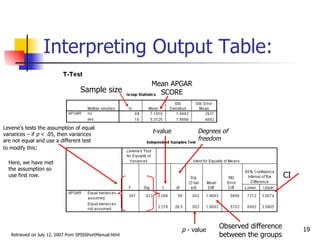
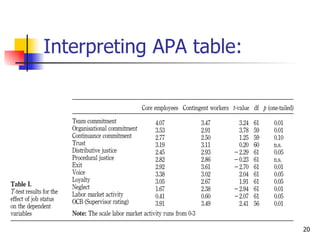
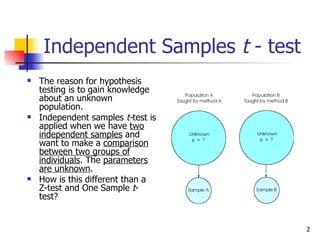
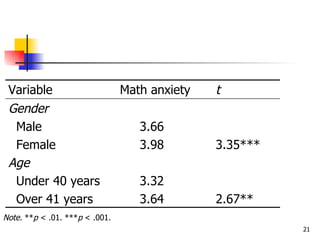An independent t-test is used to compare the means of two independent groups on a continuous dependent variable. It tests if there is a statistically significant difference between the population means of the two groups. The test assumes the groups are independent, the dependent variable is normally distributed for each group, and the groups have equal variances. To perform the test, the researcher states the hypotheses, sets an alpha level, calculates the t-statistic and degrees of freedom, and determines whether to reject or fail to reject the null hypothesis by comparing the t-statistic to the critical value.

1. Week 9:Independent t -test
t test for Two Independent Samples
1

2. Independent Samples t - test
 The reason for hypothesis
testing is to gain knowledge
about an unknown
population.
 Independent samples t-test is
applied when we have two
independent samples and
want to make a comparison
between two groups of
individuals. The parameters
are unknown.
 How is this different than a
Z-test and One Sample t-
test?
2

3. Independent t - test
 We are interested in the difference between
two independent groups. As such, we are
comparing two populations by evaluating the
mean difference.
 In order to evaluate the mean difference
between two populations, we sample from
each population and compare the sample
means on a given variable.
 Must have two independent groups
(i.e.samples) and one dependent variable that
is continuous to compare them on.
3

4. Examples:
 Do males and females significantly differ on
their level of math anxiety?
IV: Gender (2 groups: males and females)
DV: Level of math anxiety
 Do older people exercise significantly less
frequently than younger people?
IV: Age (2 groups: older people and younger
people)
DV: Frequency of getting exercise
4

5. Examples:
 Do 8th graders have significantly more
unexcused absences than 7th graders in
Toledo junior highs?
IV: Grade (2 groups: 8th grade and 7th grade)
DV: Unexcused absences
 Note that Independent t-test can be applied
to answer each research question when the
independent variable is dichotomous with
only two groups and the dependent variable
is continuous.
5

6. Generate examples of research questions
requiring an Independent Samples t-test:
 What are some examples that you can
come up with? Remember- you need
two independent samples and one
dependent variable that is continuous.
6

7. Assumptions
 The two groups are independent of one another.
 The dependent variable is normally distributed.
 Examine skewness and kurtosis (peak) of distribution
 Leptokurtosis vs. platykurtosis vs. mesokurtosis
 The two groups have approximately equal
variance on the dependent variable. (When n1 = n2
[equal sample sizes] ,the violation of this
assumption has been shown to be unimportant.)
7

8. Steps in Independent Samples t-test
8

9. Step 1: State the hypotheses
Ho: The null hypothesis states that the two samples come from the same
population. In other words, There is no statistically significant
difference between the two groups on the dependent variable.
Symbols:
Non-directional: Ho: μ1 = μ2
Directional: H 0:µ ≥ µ1 2
or
H 0:µ ≤ µ 1 2
• If the null hypothesis is tenable, the two group means differ only by
sampling fluctuation – how much the statistic’s value varies from
sample to sample or chance.
9

10. Ha: The alternative hypothesis states that the two
samples come from different populations. In other
words, There is a statistically significant difference
between the two groups on the dependent variable.
Symbols:
Non-directional: H 1:µ ≠ µ
1 2
Directional:
H 1:µ > µ
1 2
H 1:µ < µ
1 2
10

11. Step 2: Set a Criterion for
Rejecting Ho
 Compute degrees of freedom
 Set alpha level
 Identify critical value(s)
 Table C. 3 (page 638 of text)
11

12. Computing Degrees of Freedom
Calculate degrees of freedom (df) to determine
rejection region.
n n
df = 1 + 2 − 2
-2
sample size for sample1+ sample size for sample2
• df describe the number of scores in a sample that are
free to vary.
• We subtract 2 because in this case we have 2
samples.
12

13. More on Degrees of Freedom
• In an Independent samples t-test, each
sample mean places a restriction on the
value of one score in the sample, hence
the sample lost one degree of freedom and
there are n-1 degrees of freedom for the
sample.
13

14. Set alpha level
 Set at .001, .01 , .05, or .10, etc.
14

15. Identify critical value(s)
 Directional or non-directional?
 Look at page 638 Table C.3.
 To determine your CV(s) you need to
know:
 df – if df are not in the table, use the next
lowest number to be conservative
 directionality of the test
 alpha level
15

16. Step 3: Collect data and Calculate t
statistic
t= x −x 1 2
 ( − 1) + ( − 1)  1
2 2

variance
s n
1 1 s n  + 1
2 2 
 n +n −2  n n 
 1 2  1 2
Whereby:
n: Sample size s2 = variance df
x :Sample mean subscript1 = sample 1 or group 1
subscript2 = sample 2 or group 2 16

17. Step 4: Compare test statistic to
criterion
df = 18 α = .05 , two-tailed test in this example
• critical values are ± 2.101 in this example
17

18. Step 5: Make Decision
Fail to reject the null hypothesis and conclude that there is no statistically
significant difference between the two groups on the dependent variable,
t = , p > α.
OR
Reject the null hypothesis and conclude that there is a statistically
significant difference between the two groups on the dependent variable,
t = , p < α.
• If directional, indicate which group is higher or lower (greater, or less
18
than, etc.).

19. Interpreting Output Table:
Mean APGAR
Sample size SCORE
Levene’s tests the assumption of equal
variances – if p < .05, then variances
t-value Degrees of
are not equal and use a different test freedom
to modify this:
Here, we have met
the assumption so
use first row. CI
p - value
Observed difference 19
Retrieved on July 12, 2007 from SPSSShortManual.html between the groups

20. Interpreting APA table:
20

21. Variable Math anxiety t
Gender
Male 3.66
Female 3.98 3.35***
Age
Under 40 years 3.32
Over 41 years 3.64 2.67**
Note. **p < .01. ***p < .001.
21

22. Examples and Practice
 See attached document.
 Create the following index cards from this
lecture:
 When to conduct a t-test (purpose, conditions,
and assumptions)
 t-test statistic formula for computation
 t-test statistic formula
 df formula
22