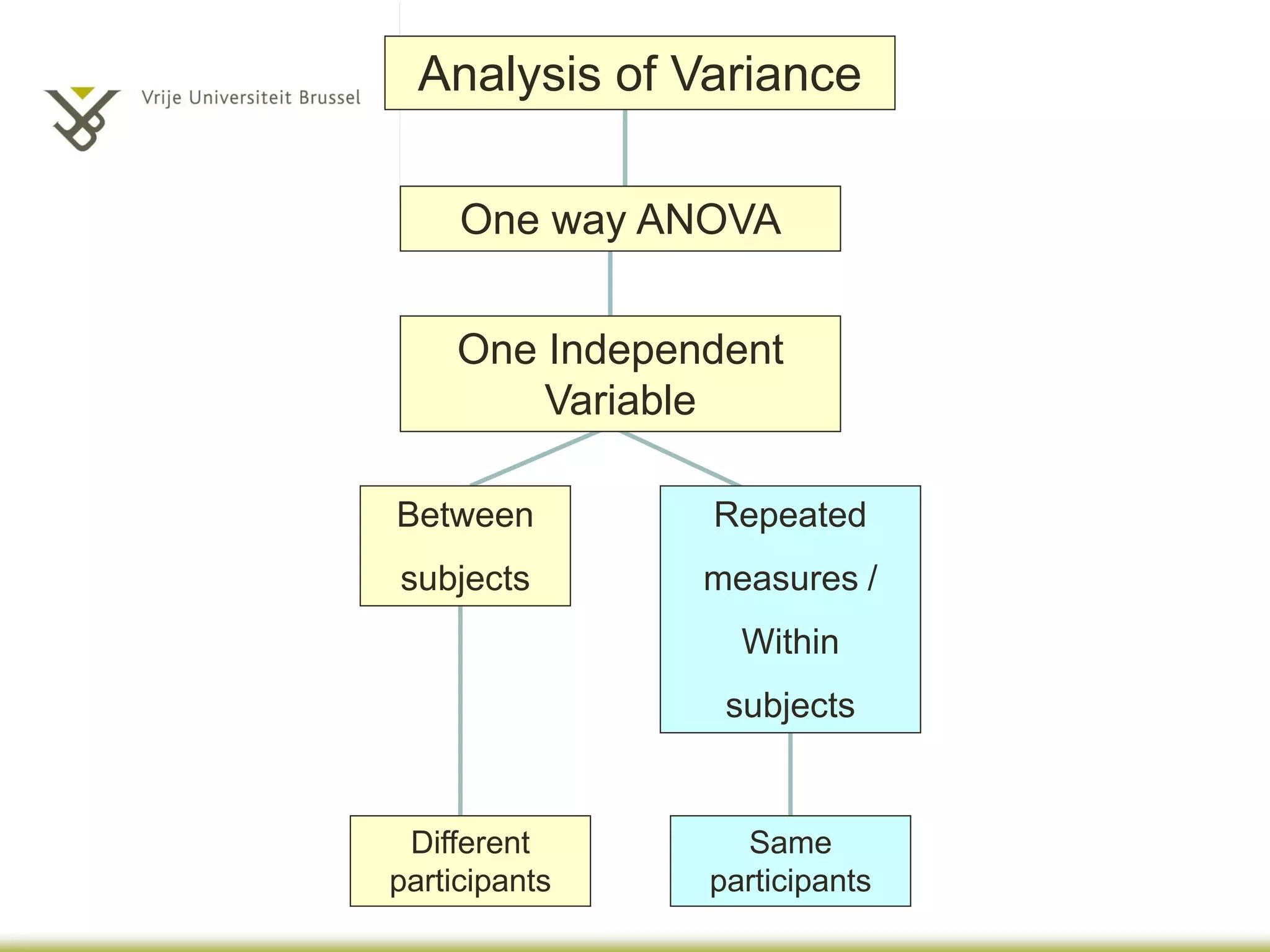
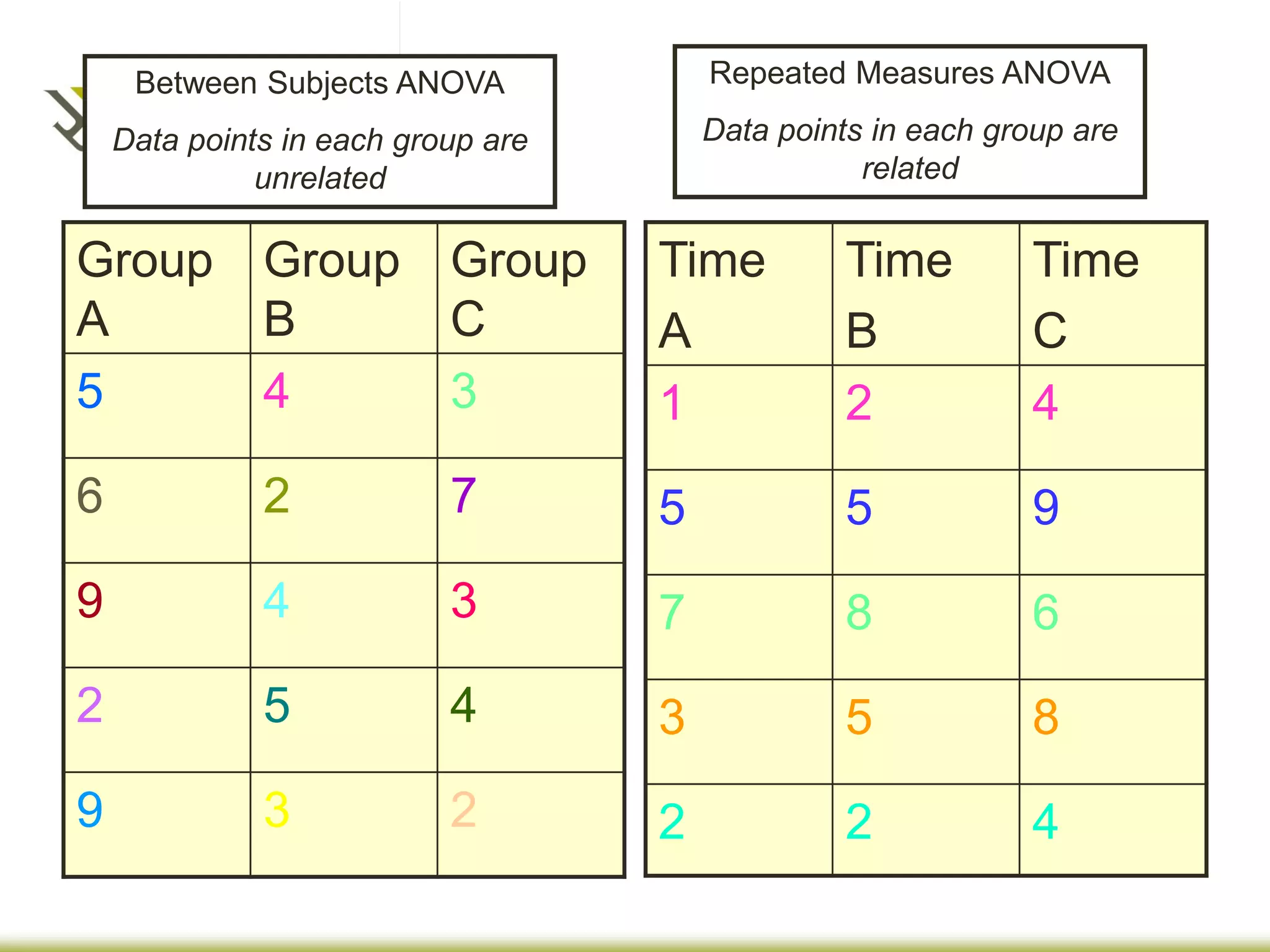
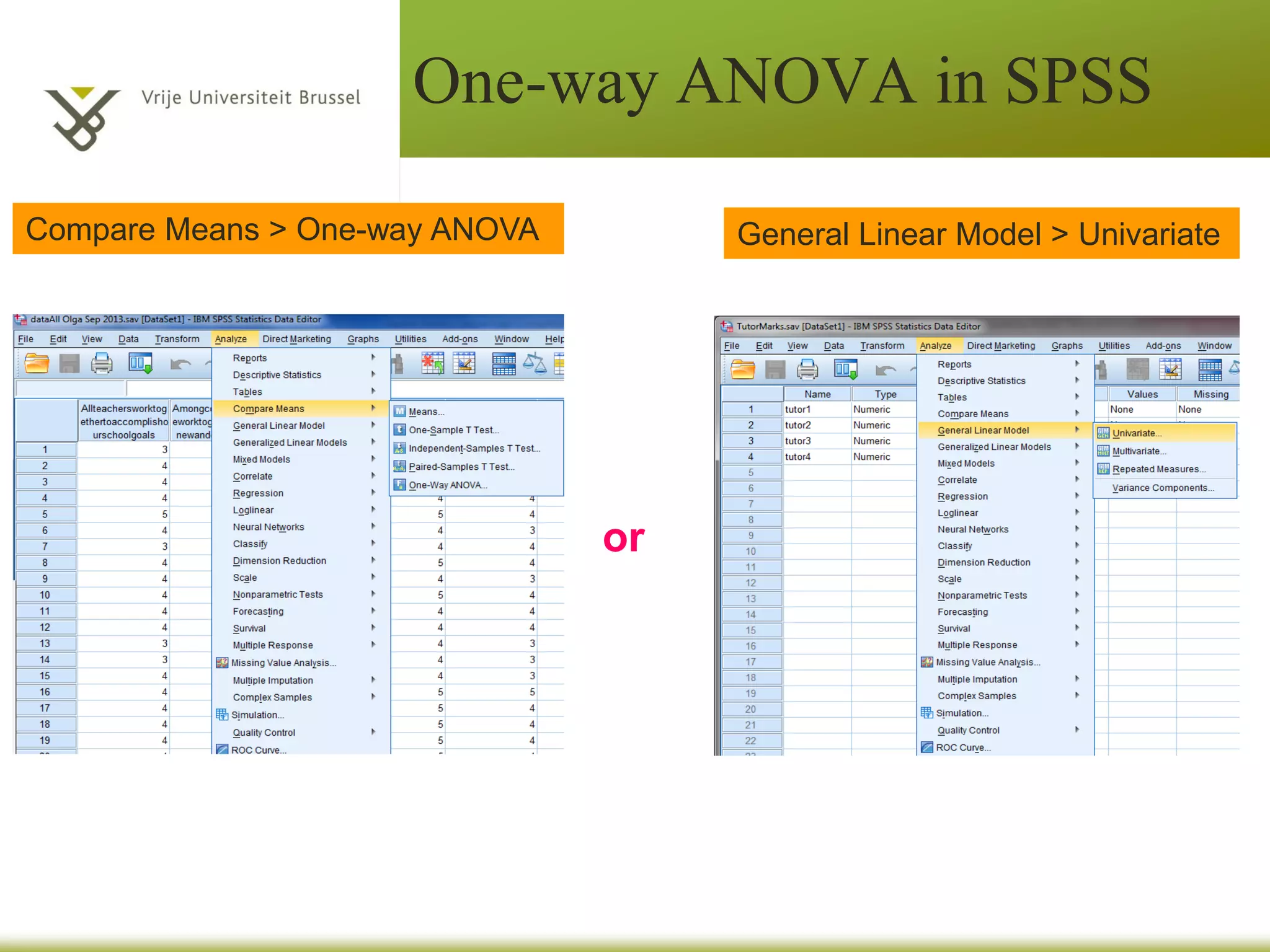
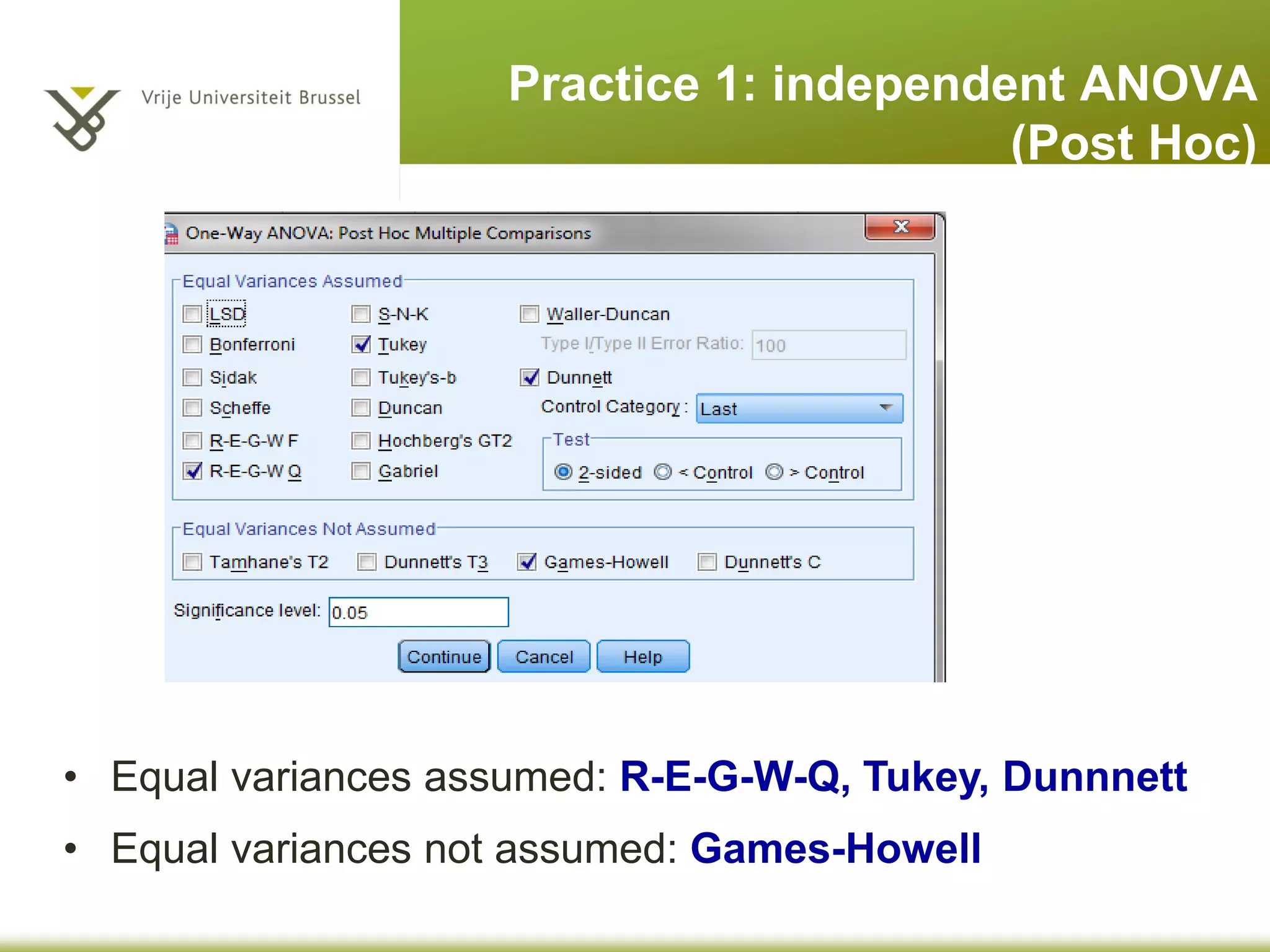
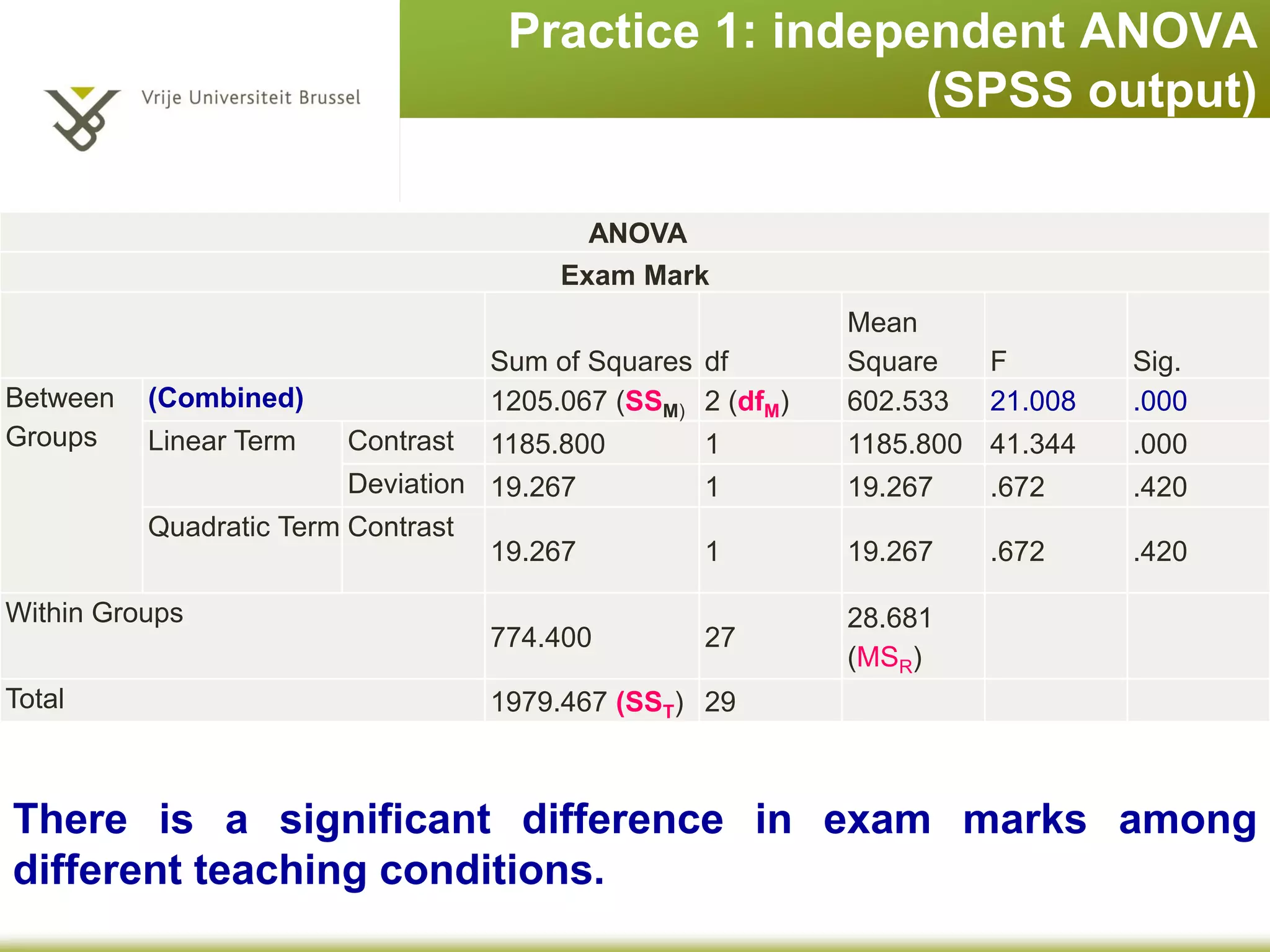
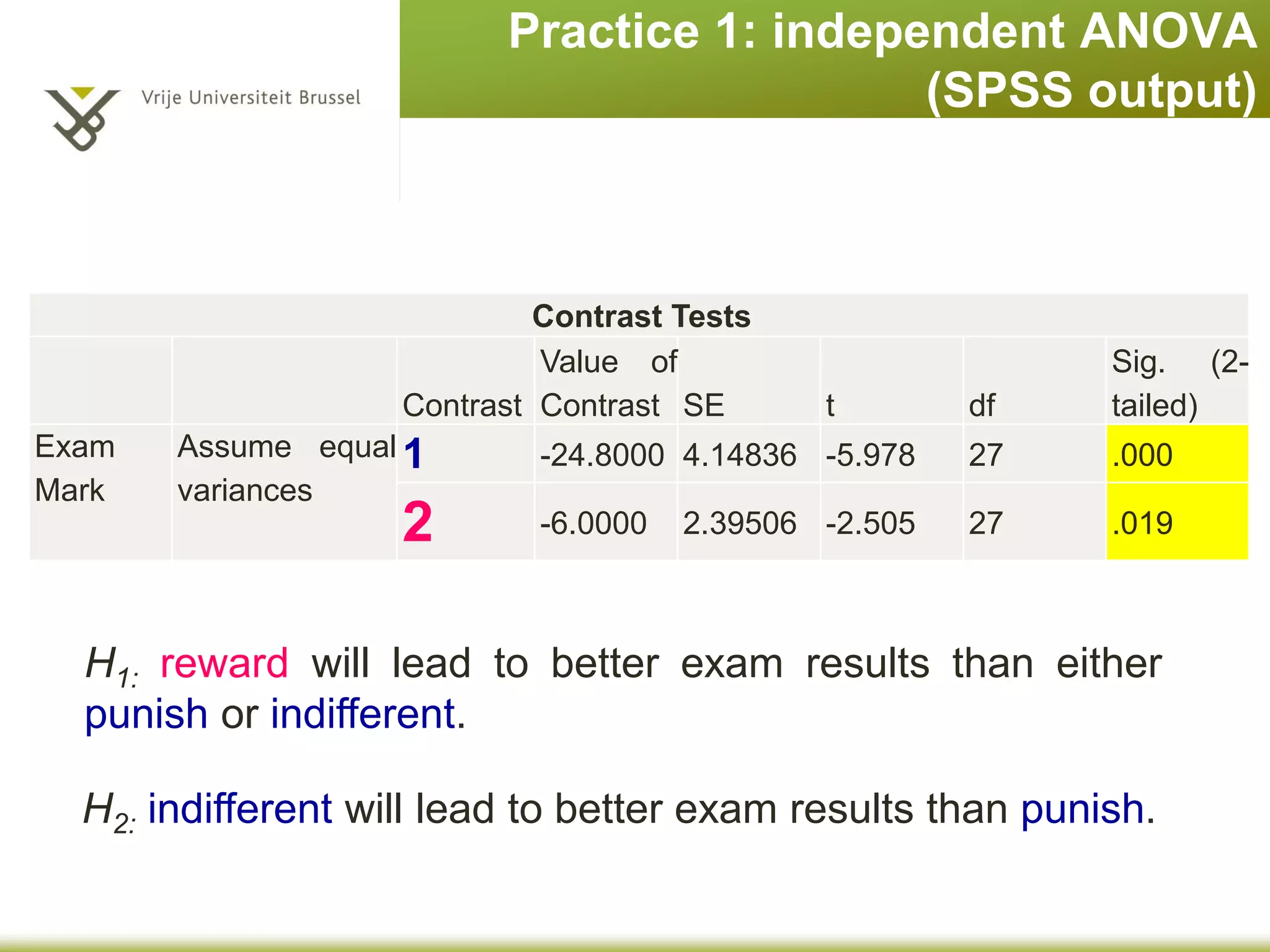
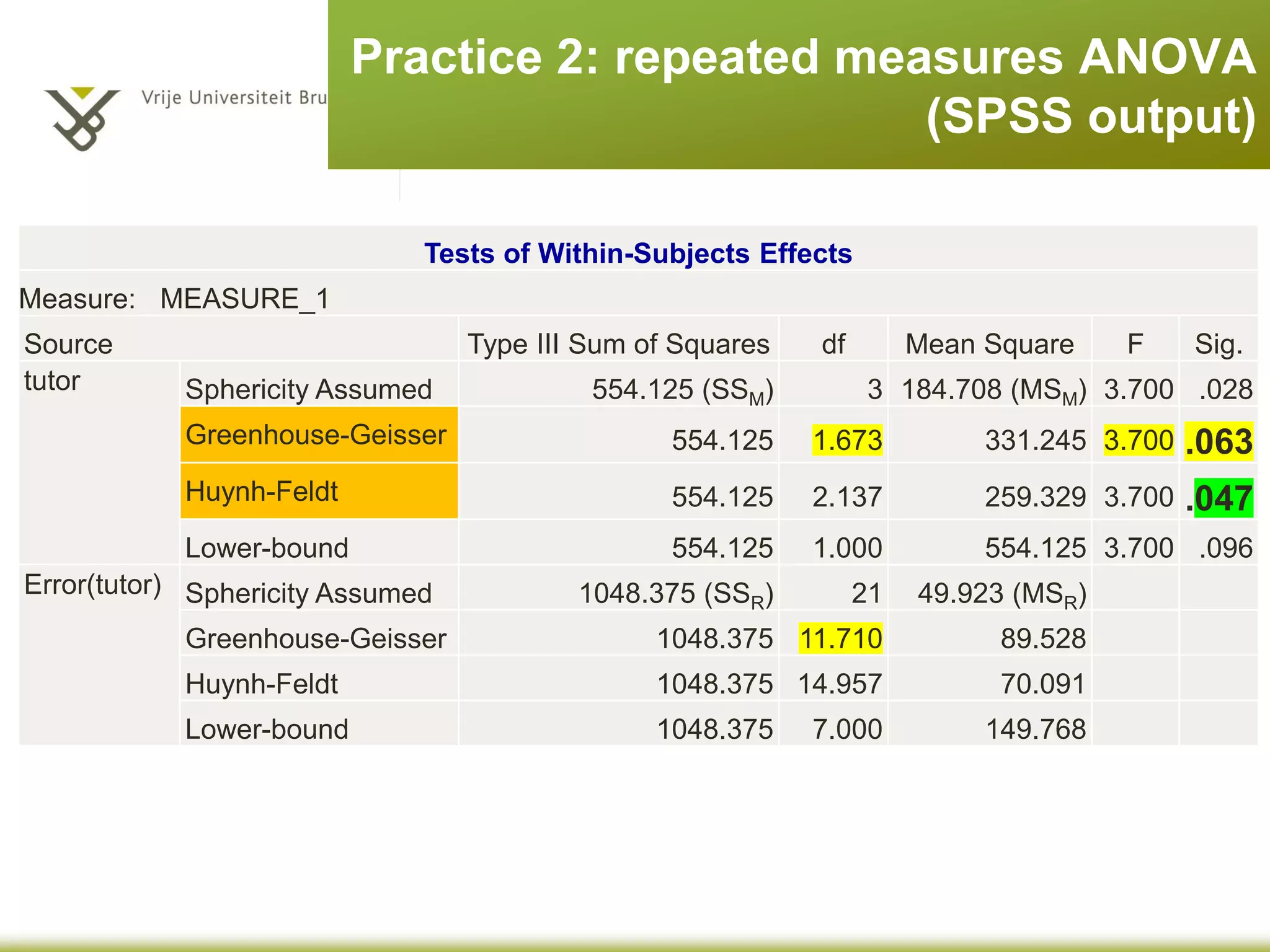
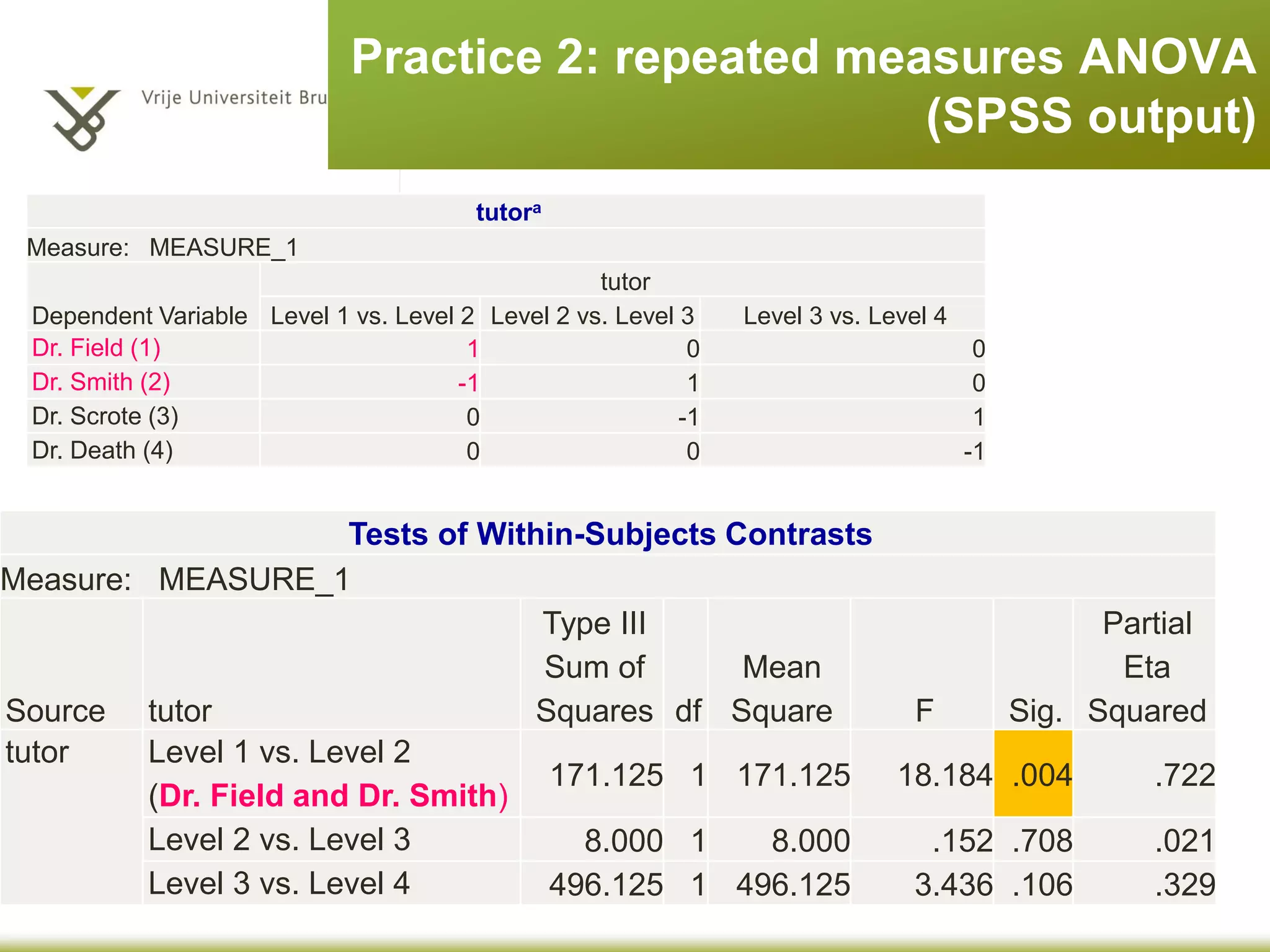
The document provides an overview of different statistical analysis methods including independent ANOVA, repeated measures ANOVA, and MANOVA. It discusses key aspects of each method such as their appropriate uses, assumptions, and how to conduct the analyses and interpret results in SPSS. For ANOVA, it covers topics like F-ratio, significance levels, post-hoc tests, effect sizes, and examples. For MANOVA, it compares it to ANOVA and explains how MANOVA can assess differences across groups on multiple dependent variables simultaneously.

1. Introduction to applied statistics
& applied statistical methods
Prof. Dr. Chang Zhu1

2. Overview
• Independent ANOVA
• Repeated measures ANOVA
• MANOVA

3. Analysis of Variance
• Enormously useful
• T-test compare two sets of scores or two
groups of participants
• ANOVA can be used for analysing more than
two groups or more than two conditions

4. Conditions before conducting
ANOVA
• The dependent variables should be interval or
ratio data
• Normal distribution of residuals
• Variances are equal

5. Analysis of Variance
One way ANOVA
One Independent
Variable
Between
subjects
Repeated
measures /
Within
subjects
Different
participants
Same
participants

6. Group
A
Group
B
Group
C
5 4 3
6 2 7
9 4 3
2 5 4
9 3 2
Time
A
Time
B
Time
C
1 2 4
5 5 9
7 8 6
3 5 8
2 2 4
Between Subjects ANOVA
Data points in each group are
unrelated
Repeated Measures ANOVA
Data points in each group are
related

7. One-way ANOVA
E.g.
• Are there differences of computer use skills
among participant groups in different study
domains?

8. One-way ANOVA
• F-ratio
F= Variance due to manipulation of IV/Error
variance
The larger the F-ratio, the greater the effect of
the IV compared to the error variance
• F (df)
• p <.05
• p<.01
• p<.001
(the means of the groups are different)

9. Post Hoc Analysis
• What ANOVA tells us:
– Rejection of the H0 tells you that there is a high
PROBABILITY that AT LEAST ONE difference
exists among the groups
• What ANOVA doesn’t tell us:
– Where the differences lie
• Post hoc analysis is needed to determine which
mean(s) is(are) different

10. One-way ANOVA post-hoc
analysis
• ANOVA determined that differences exist
among the means.
• Post hoc tests determine which means differ.

11. or
One-way ANOVA in SPSS
Compare Means > Means General Linear Model > Univariate

12. The ANOVA analysis results
• Brief report:
e.g.
• The ANOVA results show that there were
significant differences of xxxx (eg. the
powerpoint use) among the groups of
participants (F(df)=…., p<.05)

13. Results: brief example report
•Post-hoc analyses show that group x was
different to group y (mean difference=xx,
p<xx) and group z (mean difference=xx,
p<xx) ….

14. Effect size
• In experiential research, effect size is a useful measure.
• Effect size is the magnitude of the difference between groups
• For ANOVAs, the effect size can be calculated by:
r (or η: eta) , ω (omega) : effect
size
SSM: between-group effect
SST: total amount of variance in the
data
MSR: within-subject effect
dfM: degree of freedom, which is
the number of the groups minus 1
(these values are in the SPSS output)

15. Practice

16. Practice 1: independent ANOVA
H1: reward will lead to better exam
results than either punish or
indifferent.
H2: indifferent will lead to better
exam results than punish.
1
2
3

17. Practice 1: independent ANOVA
Carry out a one-way ANOVA and use planned
comparisons to test the hypotheses that
H1: reward results in better exam results than
either punishment or indifferent; and
H2: indifferent will lead to significantly better
exam results than punishment.
Analyze > Compare Means > One-way ANOVAs
The data file is teach.sav.

18. • Rule 1: We should be careful in pair selection as if we
exclude any group in one comparison, it will be excluded
in subsequent comparison as well.
• Rule 2: Groups coded with positive weights will be
compared against groups coded with negative weights.
• Rule 3: The sum of weights for a comparison should be
zero.
• Rule 4: If a group is not involved in a comparison,
automatically assign it a weight of 0.
• Rule 5: For a given contrast, the weights assigned to the
group(s) not included in the contrast should be equal to
the number of groups included in the pair comparison.
(Field, 2009)
Practice 1: independent ANOVA
rules for contrast weights

19. Practice 1: independent ANOVA
H2: indifferent will lead
to better exam results
than punish.
H1: reward will lead to
better exam results
than either punish or
indifferent.
contrast 1 condition contrast 2
1 punish (1) 1
1 indifferent (2) -1
-2 reward (3) 0

20. Practice 1: independent ANOVA
(Post Hoc)
• Equal variances assumed: R-E-G-W-Q, Tukey, Dunnnett
• Equal variances not assumed: Games-Howell

21. Practice 1: independent ANOVA
(SPSS output)
ANOVA
Exam Mark
Sum of Squares df
Mean
Square F Sig.
Between
Groups
(Combined) 1205.067 (SSM) 2 (dfM) 602.533 21.008 .000
Linear
Term
Contrast 1185.800 1 1185.800 41.344 .000
Deviation 19.267 1 19.267 .672 .420
Quadratic
Term
Contrast
19.267 1 19.267 .672 .420
Within Groups
774.400 27
28.681
(MSR)
Total 1979.467 (SST) 29
There is a significant difference in exam marks among
different teaching conditions.

22. Practice 1: independent ANOVA
(SPSS output)
Contrast Tests
Contrast
Value of
Contrast SE t df
Sig. (2-
tailed)
Exam
Mark
Assume equal
variances
1 -24.8000 4.14836 -5.978 27 .000
2 -6.0000 2.39506 -2.505 27 .019
H1: reward will lead to better exam results than either
punish or indifferent.
H2: indifferent will lead to better exam results than punish.

23. Practice 1: independent ANOVA
(report)
There was a significant effect of teaching conditions on exam
marks, F (2, 27) = 21.01, p < .001, ω = .76. Planned
contrasts revealed that reward produced significantly better
exam grades than punishment and indifference, t (27) = -
5.978, p < .01, r = .75 and that punishment produced
significantly lower exam marks than indifference, t (27) = -
2.51, p < .05, r = .43.

24. Independent vs. Repeated measures
ANOVA
• There are two possible scenarios when
obtaining various sets of data for comparison:
– Independent samples: The data in the first sample
is completely independent from the data in the
other samples.
– Dependent/Related samples: The sets of data are
dependent on one another. There is a relationship
between/among the sets of data.

25. • Three or more data sets?
– If three or more sets of data are
independent of one another Analysis of
Variance Independent (ANOVA)?
– If three or more sets of data are dependent
on one another Repeated Measures
ANOVA
Independent vs. Repeated measures
ANOVA
D1

26. Slide 25
D1 Dear Prof. shoud we changed to: Independent ANOVA?
DiepNguyet, 10/12/2014

27. Post hoc testing
• Significant F value
– At least one condition mean is significantly different from
the others
• But which one?
• Post hoc tests
– Bonferroni
– Tukey
– Sidak
– ….

28. Practice 2: repeated measures ANOVA
Tutors Essays
1. Dr Field 8
2. Dr Smith 8
3. Dr. Scrote 8
4. Dr. Deadth 8
Are there significant differences in the essay marking
among the tutors?
Analyze > General Linear Model > Repeated Measures
The data file is TutorMarks.sav.

29. Practice 2: repeated measures ANOVA
(SPSS output)
Tests of Within-Subjects Effects
Measure: MEASURE_1
Source Type III Sum of Squares df Mean Square F Sig.
tutor Sphericity Assumed 554.125 (SSM) 3 184.708 (MSM) 3.700 .028
Greenhouse-Geisser 554.125 1.673 331.245 3.700 .063
Huynh-Feldt 554.125 2.137 259.329 3.700 .047
Lower-bound 554.125 1.000 554.125 3.700 .096
Error(tutor) Sphericity Assumed 1048.375 (SSR) 21 49.923 (MSR)
Greenhouse-Geisser 1048.375 11.710 89.528
Huynh-Feldt 1048.375 14.957 70.091
Lower-bound 1048.375 7.000 149.768

30. Practice 2: repeated measures ANOVA
(SPSS output)
Tests of Within-Subjects Contrasts
Measure: MEASURE_1
Source tutor
Type III
Sum of
Squares df
Mean
Square F Sig.
Partial
Eta
Squared
tutor Level 1 vs. Level 2
(Dr. Field and Dr. Smith)
171.125 1 171.125 18.184 .004 .722
Level 2 vs. Level 3 8.000 1 8.000 .152 .708 .021
Level 3 vs. Level 4 496.125 1 496.125 3.436 .106 .329
tutora
Measure: MEASURE_1
Dependent Variable
tutor
Level 1 vs. Level 2 Level 2 vs. Level 3 Level 3 vs. Level 4
Dr. Field (1) 1 0 0
Dr. Smith (2) -1 1 0
Dr. Scrote (3) 0 -1 1
Dr. Death (4) 0 0 -1

31. Practice 2: repeated measure ANOVA
(report)
Mauchly’s test indicated that the assumption of sphericity had
been violated, χ² (5) = 11.63, p < .05, therefore degrees of
freedom were corrected using Greenhouse-Geisser
estimates of sphericity (ε = .556). The results show that there
were no significant differences in essay marking among the
tutors, F (1.67, 11.71) = 3.7, p > .05.

32. MANOVA
• One-Way Multivariate Analysis of Variance
– Multivariate analysis of variance (MANOVA) is a
multivariate extension of analysis of variance.
– As with ANOVA, the independent variables for a
MANOVA are factors, and each factor has two or
more levels.
– Unlike ANOVA, MANOVA includes multiple
dependent variables rather than a single dependent
variable.
– MANOVA evaluates whether the population
means on a set of dependent variables vary across
levels of a factor or factors.

33. MANOVA
• Understanding One-Way MANOVA
–A one-way MANOVA tests the
hypothesis that the population means
for the dependent variables are the
same (or not) for all levels of the factor,
that is, across all groups.

34. MANOVA
– If a one-way MANOVA is significant,
follow-up analyses can assess whether there
are differences among groups on the
population means on certain dependent
variables and on particular linear
combinations of dependent variables.
– The most popular follow-up approach is to
conduct multiple ANOVAs, one for each
dependent variable.

35. ANOVA vs. MANOVA
• In all cases ANOVAs have only 1 dependent
variable (they are univariate tests)
• When you have more than 1 related dependent
variables you need to conduct a MANOVA
– 2 or more DVs (interval / ratio)
– 1 or more categorical IVs
• MANOVA can be one-way, two-way,
between-groups, repeated measures and mixed

36. ANOVA vs. MANOVA
• Why not multiple ANOVAs?
• ANOVAs run separately cannot take into
account the pattern of covariation among the
dependent measures
– It may be possible that multiple ANOVAs may show no
differences while the MANOVA brings them out.
– MANOVA is sensitive not only to mean differences but
also to the direction and size of correlations among the
dependent variables.

37. MANOVA
• an extension of ANOVA in which main effects
and interactions are assessed on a combination
of DVs.
• MANOVA tests whether mean differences
among groups on a combination of DVs is
likely to occur (by chance or not).

38. MANOVA
– SPSS reports a number of statistics to
evaluate the MANOVA hypothesis, labeled
Wilks’ Lambda, Pillai’s Trace, Hotelling’s
Trace, and Roy’s Largest Root.
• Each statistic evaluates a multivariate
hypothesis that the population means are equal.
• We will use Wilks’ lambda (Λ) because it is
frequently reported in social science and
business literatures.
• Pillai’s trace (V) is a reasonable alternative to
Wilks’ lambda.

39. Interpretation of the output
2 important tables:
• Multivariate tests
– Wilks’ Lambda (most commonly used)
– Pillai’s Trace (most robust)
(see Tabachnick & Fidell, 2007)
• Tests of between-subjects effects (ANOVAs)
– Use a Bonferroni Adjustment
– Check Sig. column

40. Interpretation of the output
• Effect size
– Partial Eta Squared: the proportion of the variance in the
DV that can be explained by the IV (see Cohen, 1988)
• Comparing group means
– Estimated marginal means
• Follow-up analyses
(see Hair et al., 1998; Weinfurt, 1995)
Weinfurt, K. P. (1995). Multivariate analysis of variance.
In L. G. Grimm, & P. R. Yarnold (Eds.), Reading and understanding multivariate
statistics. Washington, DC: APA. [QA278 .R43 1995]

41. Post-hoc analysis
• If the multivariate test chosen is significant,
you’ll want to continue your analysis to discern
the nature of the differences.
• A first step would be to check the plots of mean
group differences for each DV.
• Graphical display will enhance interpretability
and understanding of what might be going on
(however it is still in ‘univariate’ mode).
• A discriminant analysis following a MANOVA
is also recommended.

42. Practice 3: MANOVA
Five knowledge tests
1.Exper (experimental psychology
such as cognitive and
neuropsychology etc.)
2.Stats (statistics);
3.Social (social psychology);
4.Develop (developmental
psychology);
5.Person (personality).
Three cohorts:
•First year
•Second year
•Third year
Are there are overall group differences along these five
measures?
The data file is
psychology.sav.

43. Practice 3: MANOVA
Five knowledge tests
1.Exper (experimental psychology
such as cognitive and
neuropsychology etc.)
2.Stats (statistics);
3.Social (social psychology);
4.Develop (developmental
psychology);
5.Person (personality).
Three cohorts:
•First year
•Second year
•Third year
Are there are overall group differences along these five
measures?
The data file is
psychology.sav.
Analyze > General Linear Model > Multivariate

44. Practice 3: MANOVA
(report)
Using Pillai’s trace, there was a significant difference in the
scores on the five knowledge tests among the first, second,
and third year students, V = .51, F (10, 68) = 2.33, p < .05.

45. Assignment 8
• Detail:
Lecture 8_practical guidelines_assignment
(p. 17)

46. • Questions?
45