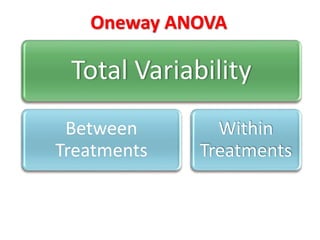
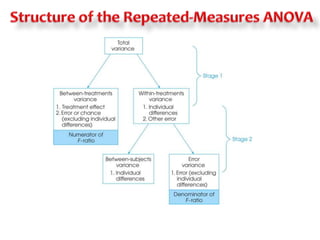
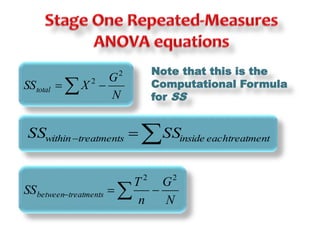
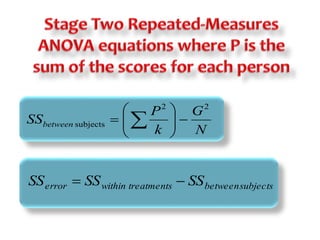
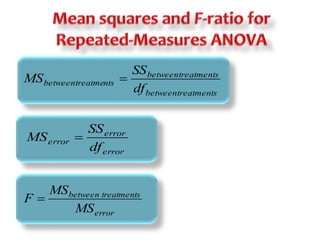
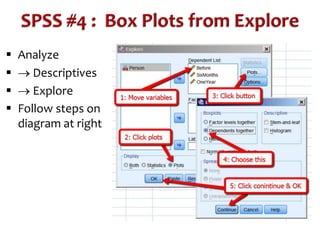
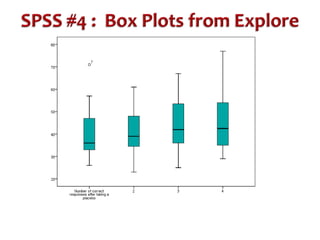
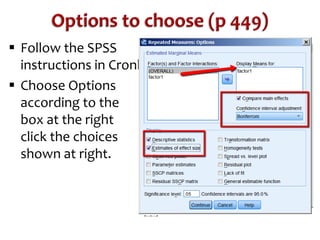
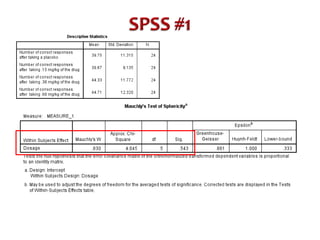
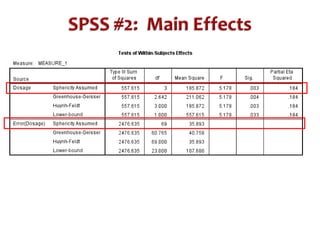
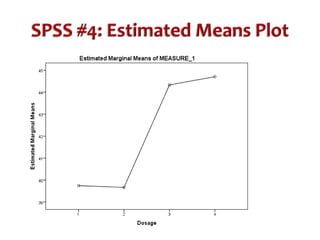
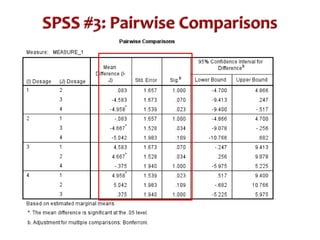
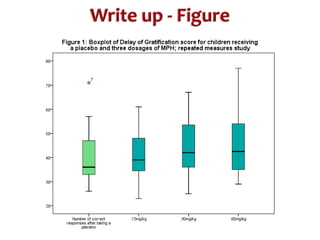
This document discusses repeated measures designs and analyzing data from such designs using repeated measures ANOVA. It explains that repeated measures ANOVA involves comparing measures taken from the same subjects across different treatment conditions while controlling for individual differences. The document provides details on the null and alternative hypotheses, calculating variance components, and assumptions of repeated measures ANOVA.

1. • Repeated measures
• Matched samples

2.  Independent-measures analysis of
variance
 Repeated measures designs
 Individual differences

3. Oneway ANOVA
Total Variability
Between
Treatments
Within
Treatments

4.  Independent Samples
 Compare two groups
that are unrelated to
each other
 Numerator is
difference between
groups
 Does not control for
the impact of
individual differences
 Related Samples
 Compare two
measures from one
person or one related
pair of people
 Numerator is
difference within pair
 Controls for the impact
of individual
differences

5.  Null hypothesis: in the population, there are no
mean differences among the treatment groups
: ... 0 1 2 3 H   
 Alternate hypothesis states that there are
mean differences among the treatment groups.
H1: At least one treatment mean μ
is different from another

6.  F ratio based on variances
variance (differences) between treatments
variance (differences) expected with no treatment effect,
(individua l difference s removed)
F 
• Same structure as independent measures
• Variance due to individual differences is
not present

7.  Participant characteristics that vary from
one person to another.
• Not systematically present in any treatment
group or by research design
 Characteristics may influence
measurements on the outcome variable
• Eliminated from the numerator by
the research design
• Must be removed from the denominator
statistically

8.  Numerator of the F ratio includes
• Systematic differences caused by treatments
• Unsystematic differences caused by random
factors (reduced because same individuals in
all treatments)
 Denominator estimates variance
reasonable to expect from unsystematic
factors
• Effect of individual differences is removed
• Residual (error) variance remains

9. Repeated Measures ANOVA
Total Variability
Between
Treatments
Within
Treatments
Between
Subjects
Error
Variance

11.  (Equations follow)
 First stage
• Identical to independent samples ANOVA
• Compute SSTotal =
SSBetween treatments + SSWithin treatments
 Second stage
• Removing the individual differences from the
denominator
• Compute SSBetween subjects and subtract it from
SSWithin treatments to find SSError

12. G
N
SS X total
2
2  
Note that this is the
Computational Formula
for SS
 withintreatments inside each treatment SS SS
G
N
T
n
SS between treatments
2 2
  

13. G
N
P
k
SSbetween
2 2


 
subjects   

 

error within treatments between subjects SS  SS  SS

14. dftotal = N – 1
dfwithin treatments = Σdfinside each treatment
dfbetween treatments = k – 1
dfbetween subjects = n – 1
dferror = dfwithin treatments – dfbetween subjects

15. MS 
error
SS
error
MS 
error df
between treatments
SS
between treatments
between treatments df
between treatments
MS
error
MS
F 

17. OVERVIEW
This study investigated the cognitive effects of stimulant
medication in children with mental retardation and
Attention-Deficit/Hyperactivity Disorder. This case study
shows the data for the Delay of Gratification (DOG) task.
Children were given various dosages of a drug,
methylphenidate (MPH) and then completed this task as
part of a larger battery of tests. The order of doses
was counterbalanced so that each dose appeared equally
often in each position. For example, six children received
the lowest dose first, six received it second, etc. The
children were on each dose one week before testing.

18. This task, adapted from the preschool delay task of the
Gordon Diagnostic System (Gordon, 1983), measures the
ability to suppress or delay impulsive behavioral responses.
Children were told that a star would appear on the
computer screen if they waited “long enough” to press a
response key. If a child responded sooner in less than four
seconds after their previous response, they did not earn a
star, and the 4-second counter restarted. The DOG
differentiates children with and without ADHD of normal
intelligence (e.g., Mayes et al., 2001), and is sensitive to
MPH treatment in these children (Hall & Kataria, 1992).

19. QUESTIONS TO ANSWER
Does higher dosage lead to higher cognitive performance
(measured by the number of correct responses to the DOG
task)?
DESIGN ISSUES
This is a repeated-measures design because each
participant performed the task after each dosage.

20. VARIABLE DESCRIPTION
d0 Number of correct responses after taking a placebo
d15
Number of correct responses after
taking .15 mg/kg of the drug
d30
Number of correct responses after
taking .30 mg/kg of the drug
d60
Number of correct responses after
taking .60 mg/kg of the drug

21.  Analyze
  Descriptives
  Explore
 Follow steps on
diagram at right

23.  Much more output than you want
 Need to ask for some Options to get SPSS to do
as much of the work as possible.
• Descriptives
• Plots
• Multiple Comparisons
• Effect Size

24.  Follow the SPSS
instructions in Cronk
 Choose Options
according to the
box at the right
click the choices
shown at right.

28.  Percentage of variance explained by the
treatment differences
 Partial η2 is percentage of variability that has
not already been explained by other factors
between treatments
error
between treatments
SS
total between subjects
SS
SS
SS SS


 2 

29.  Determine exactly where significant
differences exist among more than two
treatment means
• Tukey’s HSD can be used (almost always
same number of subjects) or Scheffé if
dropouts mean unequal measures.
• Substitute SSerror and dferror in the formulas

31. Does methylphenidate (MPH) have an impact on Delay of
Gratification for children with a diagnosis of ADHD?
Researchers compared DOG for of 24 children when they
received a placebo (M=39.75, s=11.315) and doses of 15mg/kg
(M=39.67, s=9.135), .30mg/kg (M=____, s=__) and .60mg/kg
(M=___, s=__); see Figure 1. The differences were/were not
significant (F(__ ,__)=______, p = _____). Post-hoc tests
with Bonferroni correction showed that ____________ The
impact of the MPH dosage was _____, with about ____% of
the variability in DOG related to the dosage of MPH (partial
2=._____). Dosage of MPH ______________

33.  The observations within each treatment
condition must be independent.
 The population distribution within each
treatment must be normal.
 The variances of the population
distribution for each treatment should be
equivalent.

34. • Repeated measures
• Matched samples