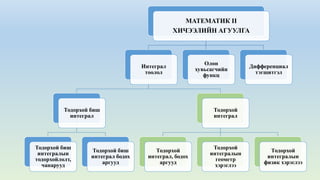
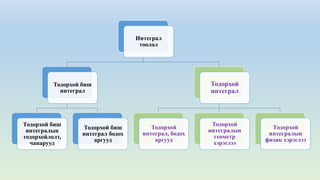
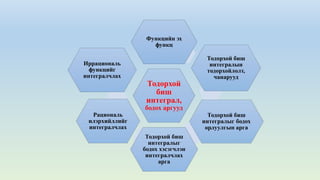
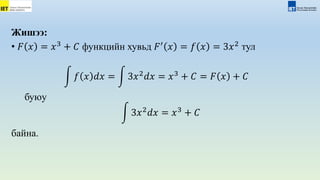This document provides an overview of the course "Mathematics II". It lists topics that will be covered including integrals, types of integrals, properties of integrals, and functions. The course is worth 3 credits and will be taught over 32 hours with 2 hours of lectures and 2 hours of seminars each week. Some key topics are definite integrals, indefinite integrals, and properties and applications of integrals in geometry and physics.