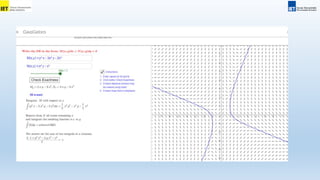
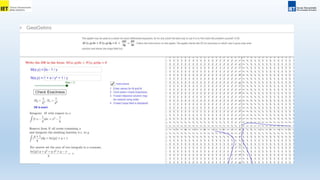
1. The document discusses complete differential equations and their integrals. It provides an example of solving the complete differential equation 2 − 9xy2dx + (4y2 − 6x3)dy = 0 for the integral u(x,y).
2. It explains that if a differential equation can be written as the complete differential of some function u, then the integral is a function of x and y alone.
3. Methods for finding the integrating factor μ(x,y) are presented to transform a given differential equation into a complete differential equation, including the possibility that μ depends only on x or y.