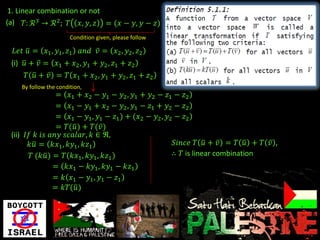
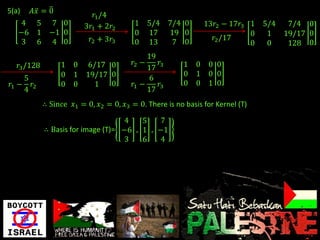
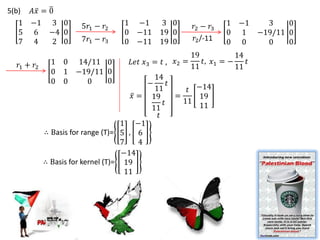
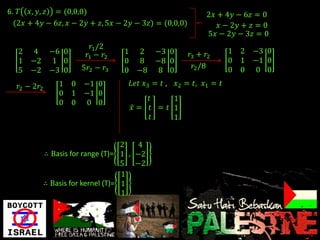
This document contains a summary of the key points from a linear algebra tutorial: 1. It provides examples of determining whether a transformation T is a linear combination or not based on checking if T(u+v)=T(u)+T(v) and T(ku)=kT(u). 2. It examines the relationship between compositions of transformations T1 and T2. 3. It explores the basis for the kernel and range of various linear transformations. 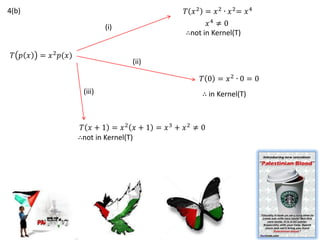4. It works through examples of determining the basis for the kernel and range of specific transformations.

2. FINAL TUTORIAL
MTH3201 LINEAR ALGEBRA

3. 1. Linear combination or not
(a) 𝛵: ℛ 3 → ℛ 2 ; 𝛵 𝑥, 𝑦, 𝑧 = (𝑥 − 𝑦, 𝑦 − 𝑧)
Condition given, please follow
𝐿𝑒𝑡 𝑢 = 𝑥1 , 𝑦1 , 𝑧1 𝑎𝑛𝑑 𝑣 = 𝑥2 , 𝑦2 , 𝑧2
(i) 𝑢 + 𝑣 = 𝑥1 + 𝑥2 , 𝑦1 + 𝑦2 , 𝑧1 + 𝑧2
𝛵 𝑢 + 𝑣 = 𝛵 𝑥1 + 𝑥2 , 𝑦1 + 𝑦2 , 𝑧1 + 𝑧2
By follow the condition,
= 𝑥1 + 𝑥2 − 𝑦1 − 𝑦2 , 𝑦1 + 𝑦2 − 𝑧1 − 𝑧2
= 𝑥1 − 𝑦1 + 𝑥2 − 𝑦2 , 𝑦1 − 𝑧1 + 𝑦2 − 𝑧2
= 𝑥1 − 𝑦1 , 𝑦1 − 𝑧1 ) + (𝑥2 − 𝑦2 , 𝑦2 − 𝑧2
= 𝛵(𝑢) + 𝛵(𝑣)
(ii) 𝐼𝑓 𝑘 𝑖𝑠 𝑎𝑛𝑦 𝑠𝑐𝑎𝑙𝑎𝑟, 𝑘 ∈ ℜ,
𝑘𝑢 = 𝑘𝑥1 , 𝑘𝑦1 , 𝑘𝑧1 𝑆𝑖𝑛𝑐𝑒 𝛵 𝑢 + 𝑣 = 𝛵 𝑢 + 𝛵 𝑣 ,
𝛵 (𝑘𝑢) = 𝛵 𝑘𝑥1 , 𝑘𝑦1 , 𝑘𝑧1 ∴ 𝛵 is linear combination
= 𝑘𝑥1 − 𝑘𝑦1 , 𝑘𝑦1 − 𝑘𝑧1
= 𝑘 𝑥1 − 𝑦1 , 𝑦1 − 𝑧1
= 𝑘𝛵(𝑢 )

4. 1. Linear combination or not
𝑥 𝑦
(d) 𝛵: ℛ 2 → ℛ; 𝛵 𝑥, 𝑦 = 𝐿𝑒𝑡 𝑢 = 𝑥1 , 𝑦1 𝑎𝑛𝑑 𝑣 = 𝑥2 , 𝑦2
𝑥+ 𝑦 𝑥− 𝑦
Condition given, please follow
(i) 𝑢 + 𝑣 = 𝑥1 + 𝑥2 , 𝑦1 + 𝑦2 , 𝛵 𝑢 + 𝑣 = 𝛵 𝑥1 + 𝑥2 , 𝑦1 + 𝑦2
𝑥 + 𝑥 𝑦1 + 𝑦2
By follow the condition,
𝛵 𝑢 + 𝑣 = 𝑥 + 𝑥1 + 𝑦2 + 𝑦 𝑥1 + 𝑥2 − 𝑦1 − 𝑦2
1 2 1 2
= 𝑥1 + 𝑥2 𝑥1 + 𝑥2 − 𝑦1 − 𝑦2 − 𝑦1 + 𝑦2 𝑥1 + 𝑥2 + 𝑦1 + 𝑦2
= 𝑥1 2 + 𝑥1 𝑥2 − 𝑥1 𝑦1 − 𝑥1 𝑦2 + 𝑥1 𝑥2 + 𝑥2 2 − 𝑥2 𝑦1 − 𝑥2 𝑦2
− 𝑦1 𝑥1 + 𝑦1 𝑥2 + 𝑦1 2 + 𝑦1 𝑦2 + 𝑦2 𝑥1 + 𝑦2 𝑥2 + 𝑦2 𝑦1 + 𝑦2 2
= 𝑥1 2 + 𝑥2 2 − 𝑦1 2 − 𝑦2 2 + 2𝑥1 𝑥2 − 2𝑦1 𝑥2 − 2𝑥1 𝑦1 − 2𝑥1 𝑦2 − 2𝑥2 𝑦1 − 2𝑥2 𝑦2
∗∗ 𝑒𝑞𝑢𝑎𝑙 𝑡𝑜 𝛵 𝑢 + 𝛵 𝑣 ? ? ?
𝛵 𝑢 + 𝛵 𝑣 = 𝛵 𝑥1 , 𝑦1 + 𝛵 𝑥2 , 𝑦2 compare
𝑥1 𝑦1 𝑥2 𝑦2
= 𝑥 + 𝑦 𝑥1 − 𝑦1 + 𝑥 + 𝑦 𝑥2 − 𝑦2
1 1 2 2
= 𝑥1 2 + 𝑥2 2 − 𝑦1 2 − 𝑦2 2 − 2𝑥1 𝑦1 − 2𝑥2 𝑦2
𝑆𝑖𝑛𝑐𝑒 𝛵 𝑢 + 𝑣 ≠ 𝛵 𝑢 + 𝛵 𝑣 , ∴ 𝛵 is not linear combination

5. 2(a) 𝛵2 ∙ 𝛵1 𝑝 𝑥 = 𝛵2 𝛵1 (𝑝 𝑥 ) 𝐶𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛 𝑔𝑖𝑣𝑒𝑛: 𝛵1 𝑝(𝑥) = 𝑝 𝑥 − 1 ,
= 𝛵2 𝑝(𝑥 − 1) 𝛵2 𝑝 𝑥 = 𝑝 𝑥 + 2
= 𝑝(𝑥 − 1 + 2)
= 𝑝(𝑥 + 1)
(b) 𝛵1 ∙ 𝛵2 𝑝 𝑥 = 𝛵1 𝛵2 (𝑝 𝑥 )
= 𝛵1 𝑝(𝑥 + 2)
= 𝑝(𝑥 + 2 − 1)
= 𝑝(𝑥 + 1)

6. 3(a) 𝑎 𝑏 𝑎 𝑏 𝑎 𝑐
𝛵1 ∙ 𝛵2 = 𝛵1 𝛵2 = 𝛵1 = 𝑎 − 𝑐 + 4𝑏 − 𝑑
𝑐 𝑑 𝑐 𝑑 𝑏 𝑑
𝑎 𝑏
𝐶𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛 𝑔𝑖𝑣𝑒𝑛: 𝛵1 = 𝑎 − 𝑏 + 4𝑐 − 𝑑,
𝑐 𝑑
𝑎 𝑏 𝑎 𝑐
𝛵2 =
𝑐 𝑑 𝑏 𝑑
𝑎 𝑏 𝑎 𝑏
(b) 𝛵2 ∙ 𝛵1 = 𝛵2 𝛵1 = 𝛵2 (𝑎 − 𝑏 + 4𝑐 − 𝑑)
𝑐 𝑑 𝑐 𝑑
∴ 𝑑𝑜𝑒𝑠 𝑛𝑜𝑡 𝑒𝑥𝑖𝑠𝑡, 𝑖𝑚𝑎𝑔𝑒 𝑇1 𝑛𝑜𝑡 𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑜𝑓 𝑑𝑜𝑚𝑎𝑖𝑛 𝑇2

7. 4(a) 𝑥2 𝑝 𝑥 = 𝑥2 + 𝑥
(i) 𝑝 𝑥 = 1 + 1/𝑥
𝑝 𝑥 is not in domain of 𝑝2
∴ x 2 +x is not in range(T)
𝛵 𝑝 𝑥 = 𝑥 2 𝑝(𝑥)
(ii)
𝑥2 𝑝 𝑥 = 𝑥 + 1
(iii) 𝑝 𝑥 = 1/𝑥 + 1/𝑥 2
𝑝 𝑥 is not in domain of 𝑝2
∴ x + 1 is not in range(T)
𝑥2 𝑝 𝑥 = 3 − 𝑥2
3
𝑝 𝑥 = 2−1
𝑥
𝑝 𝑥 is not in domain of 𝑝2
∴ 3 − x 2 is not in range(T)

8. 4(b) 𝛵 𝑥 2 = 𝑥 2 ∙ 𝑥 2= 𝑥 4
(i) 𝑥4 ≠ 0
∴not in Kernel(T)
𝛵 𝑝 𝑥 = 𝑥 2 𝑝(𝑥)
(ii)
𝛵 0 = 𝑥2 ∙ 0 = 0
(iii) ∴ in Kernel(T)
𝛵 𝑥 + 1 = 𝑥2 𝑥 + 1 = 𝑥3 + 𝑥2 ≠ 0
∴not in Kernel(T)

9. 5(a) 𝐴𝑥 = 0
𝑟1 /4
4 5 7 0 3𝑟1 + 2𝑟2 1 5/4 7/4 0 13𝑟2 − 17𝑟3 1 5/4 7/4 0
−6 1 −1 0 0 17 19 0 0 1 19/17 0
𝑟2 + 3𝑟3 𝑟2 /17
3 6 4 0 0 13 7 0 0 0 128 0
19
𝑟3 /128 1 0 6/17 0 𝑟2 − 𝑟 1 0 0 0
17 3
0 1 19/17 0 0 1 0 0
5 6
𝑟1 − 𝑟 0 0 1 0 𝑟1 − 𝑟 0 0 1 0
4 2 17 3
∴ Since 𝑥1 = 0, 𝑥2 = 0, 𝑥3 = 0. There is no basis for Kernel (T)
4 5 7
∴ Basis for image (T)= −6 , 1 , −1
3 6 4

10. 5(b) 𝐴𝑥 = 0
1 −1 3 0 5𝑟1 − 𝑟2 1 −1 3 0 𝑟2 − 𝑟3 1 −1 3 0
5 6 −4 0 0 −11 19 0 0 1 −19/11 0
7 4 2 0 7𝑟1 − 𝑟3 0 −11 19 0 𝑟2 /-11 0 0 0 0
19 14
𝑟1 + 𝑟2 1 0 14/11 0 𝐿𝑒𝑡 𝑥3 = 𝑡 , 𝑥2 = 𝑡, 𝑥1 = − 𝑡
11 11
0 1 −19/11 0
0 14
0 0 0 − 𝑡
11 𝑡 −14
𝑥 = 19 = 19
𝑡 11
11 11
𝑡
1 −1
∴ Basis for range (T)= 5 , 6
7 4
−14
∴ Basis for kernel (T)= 19
11

11. 6. 𝑇 𝑥, 𝑦, 𝑧 = (0,0,0) 2𝑥 + 4𝑦 − 6𝑧 = 0
(2𝑥 + 4𝑦 − 6𝑧, 𝑥 − 2𝑦 + 𝑧, 5𝑥 − 2𝑦 − 3𝑧) = (0,0,0) 𝑥 − 2𝑦 + 𝑧 = 0
5𝑥 − 2𝑦 − 3𝑧 = 0
𝑟1 /2
2 4 −6 0 𝑟1 − 𝑟2 1 2 −3 0 𝑟3 + 𝑟2 1 2 −3 0
1 −2 1 0 0 8 −8 0 0 1 −1 0
5𝑟2 − 𝑟3 𝑟2 /8 0 0 0 0
5 −2 −3 0 0 −8 8 0
𝑟2 − 2𝑟2 1 0 −1 0 𝐿𝑒𝑡 𝑥3 = 𝑡 , 𝑥2 = 𝑡, 𝑥1 = 𝑡
0 1 −1 0
𝑡 1
0 0 0 0
𝑥= 𝑡 = 𝑡 1
𝑡 1
2 4
∴ Basis for range (T)= 1 , −2
5 −2
1
∴ Basis for kernel (T)= 1
1

12. TAMAT