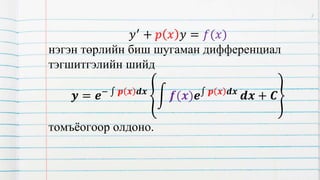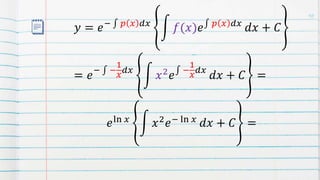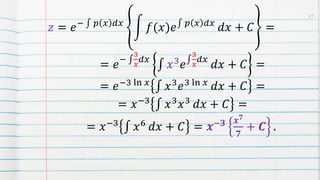1. This document discusses methods for solving first-order linear differential equations. It defines a first-order linear differential equation as one of the form y'+py=f(x).
2. It provides examples of solving homogeneous and non-homogeneous first-order linear differential equations. The general solutions are presented as y=Ce^-px + particular solutions.
3. Bernoulli differential equations of the form y'+py=f(x)y^n, n≠1 are introduced, which can be transformed into a first-order linear equation using a substitution. An example of solving a Bernoulli equation is shown.