This document provides information about digital logic design and binary logic. It discusses binary variables that can take on values of 1 or 0, and logical operations on these variables. It defines logic gates like AND, OR, and NOT and shows their truth tables. It also covers Boolean algebra, Boolean functions, canonical forms including minterms and maxterms, and properties of Boolean algebra.

1. Digital Logic Design
BINARY LOGIC, LOGIC GATES
1
4
Prepared by: Mir Omranudin Abhar
Email : MirOmran@Gmail.com
Fall ,2019

2. Binary Logic
Binary logic deals with variables that take on two discrete values and with
operations that assume logical meaning.
The two values the variables assume may be called by different names (true
and false, yes and no, etc.), but for our purpose, it is convenient to think in
terms of bits and assign the values 1 and 0.
2

3. Binary Logic
1. Binary logic consists of binary variables and a set of logical operations.
2. The variables are designated by letters of the alphabet, such as A, B, C,
x, y, z, etc., with each variable having two and only two distinct
possible values: 1 and 0.
3

4. Binary Logic [AND,OR,NOT]
4
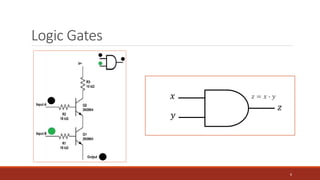
𝑥 ∙ 𝑦 = 𝑧
𝑥 𝑎𝑛𝑑 𝑦 = 𝑧
X Y Z
0 0 0
1 0 0
0 1 0
1 1 1
𝑥 + 𝑦 = 𝑧
𝑥 𝑜𝑟 𝑦 = 𝑧
X Y Z
0 0 0
1 0 1
0 1 1
1 1 1
𝑥′ = 𝑧
ҧ
𝑥 = 𝑧
X X’
0 1
1 0
AND OR NOT

5. Logic Gates
Logic gates are electronic circuits that operate on one or more input signals
to produce an output signal.
5

6. Logic Gates
6
𝑥
𝑦
𝑧
𝑧 = 𝑥 ∙ 𝑦

7. Logic Gates[AND]
7
𝑥 ∙ 𝑦 = 𝑧
𝑥 𝑎𝑛𝑑 𝑦 = 𝑧 X Y Z
0 0 0
1 0 0
0 1 0
1 1 1

8. Logic Gates[OR]
8
𝑥 + 𝑦 = 𝑧
𝑥 𝑜𝑟 𝑦 = 𝑧 X Y Z
0 0 0
1 0 1
0 1 1
1 1 1

9. Logic Gates[Not]
9
𝑥′ = 𝑧
ҧ
𝑥 = 𝑧
X X’
0 1
1 0

10. Logic Gates[Buffer]
10
𝑥 = 𝑧
X X’
0 0
1 1

11. Logic Gates[NAND]
11
𝑥 ∙ 𝑦 = 𝑧
𝑥 𝑛𝑎𝑛𝑑 𝑦 = 𝑥𝑦 ′
= 𝑧 X Y Z
0 0 1
1 0 1
0 1 1
1 1 0

12. Logic Gates[NOR]
12
𝑥 + 𝑦 ′
= 𝑧
𝑥 𝑛𝑜𝑟 𝑦 = (𝑥 + 𝑦)′ = 𝑧 X Y Z
0 0 1
1 0 0
0 1 0
1 1 0

13. Logic Gates[Exclusive-OR (XOR)]
13
𝑧 = 𝑥𝑦′
+ 𝑥′
𝑦
𝑧 = 𝑥 ⊕ 𝑦
X Y Z
0 0 0
1 0 1
0 1 1
1 1 0

14. Logic Gates[Exclusive-NOR (XNOR)]
14
𝑧 = 𝑥𝑦′
+ 𝑥′
𝑦 ′
𝑧 = 𝑥 ⊕ 𝑦 ′
X Y Z
0 0 1
1 0 0
0 1 0
1 1 1

15. 15
Boolean Algebra
𝑎 ∗ 𝑏 = 𝑐
𝑎, 𝑏, 𝑐 ∈ 𝑆
1

16. Boolean Algebra
16
Boolean algebra is an algebraic structure defined by a set of elements, B,
together with two binary operators, (+) and (∙) ,provided that the
following (Huntington) postulates are satisfied:
1. (a) The structure is closed with respect to the operator (+).
(b) The structure is closed with respect to the operator (∙).
𝑆 = 1,2,3,4, … ; 𝑎, 𝑏, 𝑐 ∈ 𝑆
𝑎 + 𝑏 ⇒ 𝑐
𝑎 ∙ 𝑏 ⇒ 𝑐

17. Boolean Algebra
17
2. (a) The element 0 is an identity element with respect to (+) ;
that is 𝑥 + 0 = 0 + 𝑥 = 𝑥.
(b) The element 1 is an identity element with respect to (∙);
that is 𝑥 ∙ 1 = 1 ∙ 𝑥 = 𝑥.
3. (a) The structure is commutative with respect to (+);
that is 𝑥 + 𝑦 = 𝑦 + 𝑥.
(b) The structure is commutative with respect to (∙);
that is 𝑥 ∙ 𝑦 = 𝑦 ∙ 𝑥.

18. Boolean Algebra
18
4. (a) The operator (∙) is distributive over (+);
that is, 𝑥 ∙ (𝑦 + 𝑧) = (𝑥 ∙ 𝑦) + (𝑥 ∙ 𝑧) .
(b) The operator (+) is distributive over (∙);
that is, 𝑥 + (𝑦 ∙ 𝑧) = (𝑥 + 𝑦) ∙ (𝑥 + 𝑧) .
5. For every element 𝑥 ∈ 𝐵, there exists an element 𝑥′ ∈ 𝐵
(called the complement of x) such that
(𝑎) 𝑥 + 𝑥′
= 1 and (𝑏) 𝑥 ∙ 𝑥′
= 0.

19. Comparing
[Boolean algebra] & [ordinary algebra]
19
1. The distributive law of (+) over (∙).
𝑥 + 𝑦 ∙ 𝑧 = 𝑥 + 𝑦 ∙ 𝑥 + 𝑧
is valid for Boolean algebra, but not for ordinary algebra.
2. Boolean algebra does not have additive or multiplicative inverses;
therefore, there are no subtraction(−) or division(÷)
operations.

20. Comparing
[Boolean algebra] & [ordinary algebra]
20
3. The Postulate 5 defines an operator called the complement that is
not available in ordinary algebra.
4. Ordinary algebra deals with the real numbers, which constitute an
infinite set of elements. Boolean algebra deals with the Binary
number, The set B is defined as a set with only two elements, 0
and 1.

21. Operator Precedence
21
The operator precedence for evaluating Boolean expressions is
• parentheses
• NOT
• AND
• OR
𝑥𝑦′
+ 𝑦 + 𝑥 + 𝑦 + 𝑥′

22. Properties of Boolean Algebra
22
1. 𝑥 + 0 = 𝑥
2. 𝑥 + 𝑥’ = 1
3. 𝑥 + 𝑥 = 𝑥
4. 𝑥 + 1 = 0
5. (𝑥’)’ = 𝑥
𝑥 ∙ 1 = 𝑥
𝑥 ∙ 𝑥’ = 0
𝑥 ∙ 𝑥 = 𝑥
𝑥 ∙ 0 = 0

23. Properties of Boolean Algebra
23
6. 𝑥 + 𝑦 = 𝑦 + 𝑥
7. 𝑥 + 𝑦 + 𝑧 = 𝑥 + 𝑦 + 𝑧
8. 𝑥 𝑦 + 𝑧 = 𝑥𝑦 + 𝑥𝑧
9. (𝑥 + 𝑦)′ = 𝑥′𝑦′
10. 𝑥 + 𝑥𝑦 = 𝑥
𝑥𝑦 = 𝑦𝑥
𝑥 𝑦𝑧 = 𝑥𝑦 𝑧
𝑥 + 𝑦𝑧 = 𝑥 + 𝑦 (𝑥 + 𝑧)
𝑥𝑦 ′ = 𝑥′ + 𝑦′
𝑥(𝑥 + 𝑦) = 𝑥

24. Boolean Function
24
Boolean algebra is an algebra that deals with binary variables and logic
operations. A Boolean function described by an algebraic expression
consists of binary variables, the constants 0 and 1, and the logic operation
symbols.
We define a literal to be a single variable within a term, in complemented
or uncomplemented form .
𝐹1 = 𝑥 + 𝑦′
𝑧

25. Boolean Function
25
𝑭𝟏 = 𝒙 + 𝒚′𝒛
𝒙 𝒚 𝒛 𝑭𝟐
0 0 0 𝟎
0 0 1 𝟏
0 1 0 𝟎
0 1 1 𝟏
1 0 0 𝟏
1 0 1 𝟏
1 1 0 𝟎
1 1 1 𝟎
[ 2 Term ] & [ 3 Literal ]

26. Boolean Function
26
𝑭𝟐 = 𝒙′𝒚′𝒛 + 𝒙′𝒚𝒛 + 𝒙𝒚′
𝒙 𝒚 𝒛 𝑭𝟐
0 0 0 𝟎
0 0 1 𝟏
0 1 0 𝟎
0 1 1 𝟏
1 0 0 𝟏
1 0 1 𝟏
1 1 0 𝟎
1 1 1 𝟎
[ 3 Term ] & [ 8 Literal ]

27. Boolean Function
27
𝑭𝟐 = 𝒙′𝒚′𝒛 + 𝒙′𝒚𝒛 + 𝒙𝒚′
𝒙 𝒚 𝒛 𝑭𝟐
0 0 0 𝟎
0 0 1 𝟏
0 1 0 𝟎
0 1 1 𝟏
1 0 0 𝟏
1 0 1 𝟏
1 1 0 𝟎
1 1 1 𝟎
𝑭𝟐 = 𝒙′𝒚′𝒛 + 𝒙′𝒚𝒛 + 𝒙𝒚′
𝑭𝟐 = 𝒙′𝒛 𝒚′ + 𝒚 + 𝒙𝒚′
𝑭𝟐 = 𝒙′𝒛(𝟏) + 𝒙𝒚′
𝑭𝟐 = 𝒙′𝒛 + 𝒙𝒚′

28. Boolean Function
28
𝑆𝑖𝑚𝑝𝑙𝑖𝑓𝑦 𝑡ℎ𝑒 𝑓𝑜𝑙𝑙𝑜𝑤𝑖𝑛𝑔 𝐵𝑜𝑜𝑙𝑒𝑎𝑛 𝑓𝑢𝑛𝑐𝑡𝑖𝑜𝑛𝑠 𝑡𝑜 𝑎 𝑚𝑖𝑛𝑖𝑚𝑢𝑚 𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑙𝑖𝑡𝑒𝑟𝑎𝑙𝑠.
1. 𝒙 𝒙′ + 𝒚 = 𝑥𝑥′ + 𝑥𝑦 = +𝑥𝑦 = 𝑥𝑦.
2. 𝒙 + 𝒙′𝒚 = 𝑥 + 𝑥′ 𝑥 + 𝑦 = 1 𝑥 + 𝑦 = 𝑥 + 𝑦.
3. 𝒙 + 𝒚 𝒙 + 𝒚′
= 𝑥 + 𝑥𝑦 + 𝑥𝑦′
+ 𝑦𝑦′
= 𝑥 1 + 𝑦 + 𝑦′
= 𝑥.
4. 𝒙𝒚 + 𝒙′𝒛 + 𝒚𝒛 = 𝑥𝑦 + 𝑥′𝑧 + 𝑦𝑧 𝑥 + 𝑥′ .
= 𝑥𝑦 + 𝑥′𝑧 + 𝑥𝑦𝑧 + 𝑥′𝑦𝑧
= 𝑥𝑦 1 + 𝑧 + 𝑥′𝑧 1 + 𝑦
= 𝑥𝑦 + 𝑥′𝑧

29. Complement of a Function
29
The complement of a function F is F’ and is obtained from an interchange of 0’s for
1’s and 1’s for 0’s in the value of F.
𝐹 = 𝐴 + 𝐵′
𝐹′ = 𝐴′𝐵
𝐹1 = 𝐴 + 𝐵′
+ 𝐶
𝐹1′ = 𝐴′𝐵𝐶
𝐹2 = 𝐴𝐵′𝐶′
𝐹2
′
= 𝐴′ + 𝐵 + 𝐶

30. Complement of a Function
30
Find the complement of the functions 𝐹1 and 𝐹2.
𝐹1 = 𝑥′𝑦𝑧′ + 𝑥′𝑦′𝑧
(𝐹1)′ = (𝑥 + 𝑦′ + 𝑧)(𝑥 + 𝑦 + 𝑧′)
𝐹2 = 𝑥 𝑦′
𝑧′
+ 𝑦𝑧
(𝐹2)′ = 𝑥′
+ 𝑦𝑧′
+ 𝑦′
𝑧

31. 31
Canonical & Standard
Forms
𝑓1 = 𝑥′
𝑦 + 𝑥𝑦 + 𝑥𝑦′
𝑓2 = (𝑥′
+𝑦)(𝑥 + 𝑦)(𝑥 + 𝑦′
)

32. Canonical Forms
32
1. Minterm
2. Maxterm
𝑓1 = 𝑥′
𝑦𝑧
𝑓1 = (𝑥′
+𝑦 + 𝑧)

33. Canonical → [Minterms]
33
A binary variable may appear either in its normal form (x) or in its
complement form(𝑥′
) .
Now consider two binary variables x and y combined with an AND
operation. Since each variable may appear in either form, there are four
possible combinations:
(𝑥′
𝑦′
),(𝑥′
𝑦) , (𝑥𝑦′
) , (𝑥𝑦)
Each of these four (AND) terms is called a minterm, or a standard products.

34. Canonical → [Minterms]
34
A minterm is a product (AND) of all variables in the function, in direct or
complemented form.
𝑥′ → 0
𝑥 → 1
𝐷𝑒𝑠𝑖𝑔𝑛𝑎𝑡𝑖𝑜𝑛: 𝑚𝑗
𝒙 𝒚 𝒛
𝑴𝒊𝒏𝒕𝒆𝒓𝒎𝒔
𝑻𝒆𝒓𝒎 𝑫𝒆𝒔𝒊𝒈𝒏𝒂𝒕𝒊𝒐𝒏
𝟎 𝟎 𝟎 𝒙′
𝒚′
𝒛′ 𝒎𝟎
𝟎 𝟎 𝟏 𝒙′𝒚′𝒛 𝒎𝟏
𝟎 𝟏 𝟎 𝒙′𝒚𝒛′ 𝒎𝟐
𝟎 𝟏 𝟏 𝒙′𝒚𝒛 𝒎𝟑
𝟏 𝟎 𝟎 x𝒚′𝒛′ 𝒎𝟒
𝟏 𝟎 𝟏 𝒙𝒚′𝒛 𝒎𝟓
𝟏 𝟏 𝟎 𝒙𝒚𝒛′ 𝒎𝟔
𝟏 𝟏 𝟏 𝒙𝒚𝒛 𝒎𝟕

35. Canonical → [maxterm]
35
(𝑥′
+𝑦′
),(𝑥′
+ 𝑦) , (𝑥 + 𝑦′
) , (𝑥 + 𝑦)
Each of these four (OR) terms is called a maxterm or a standard sums.

36. Canonical → [Maxterm]
36
A maxterm is a sum (OR) of all the variables in the function, in direct or
complemented form.
𝑥′
→ 1
𝑥 → 0
𝐷𝑒𝑠𝑖𝑔𝑛𝑎𝑡𝑖𝑜𝑛: 𝑀𝑗
𝒙 𝒚 𝒛
𝑴𝒊𝒏𝒕𝒆𝒓𝒎𝒔
𝑻𝒆𝒓𝒎 𝑫𝒆𝒔𝒊𝒈𝒏𝒂𝒕𝒊𝒐𝒏
𝟎 𝟎 𝟎 𝒙 + 𝒚 + 𝒛 𝑴𝟎
𝟎 𝟎 𝟏 𝒙 + 𝒚 + 𝒛′ 𝑴𝟏
𝟎 𝟏 𝟎 𝒙 + 𝒚′ + 𝒛 𝑴𝟐
𝟎 𝟏 𝟏 𝒙 + 𝒚′ + 𝒛′ 𝑴𝟑
𝟏 𝟎 𝟎 𝒙′ + 𝒚 + 𝒛 𝑴𝟒
𝟏 𝟎 𝟏 𝒙′ + 𝒚 + 𝒛′ 𝑴𝟓
𝟏 𝟏 𝟎 𝒙′ + 𝒚′ + 𝒛 𝑴𝟔
𝟏 𝟏 𝟏 𝒙′ + 𝒚′ + 𝒛′ 𝑴𝟕

37. Canonical Forms
37
Boolean functions expressed as a sum of minterms(SOM) or product of
maxterms(POM) are said to be in Canonical form .
𝑓1 = 𝑥′𝑦𝑧 + 𝑥𝑦𝑧 + 𝑥′𝑦′𝑧 = 𝒎𝟑 + 𝒎𝟕 + 𝒎𝟏
𝑓2 = 𝑥 + 𝑦′
+ 𝑧′
𝑥′
+ 𝑦′
+ 𝑧′
𝑥 + 𝑦 + 𝑧′
= 𝑴𝟑 + 𝑴𝟕 + 𝑴𝟏

38. Canonical → [Sum of Minterms]
38
Express the Boolean function 𝐹 = 𝐴 + 𝐵’𝐶 as a sum of minterms.
𝐹 = 𝐴 + 𝐵’𝐶
→ 𝐴 𝐵 + 𝐵′
+ 𝐵’𝐶
→ 𝐴𝐵(𝐶 + 𝐶′) + 𝐴𝐵′(𝐶 + 𝐶′) + 𝐵’𝐶(𝐴 + 𝐴′)
→ 𝐴𝐵𝐶 + 𝐴𝐵𝐶′ + 𝐴𝐵′𝐶 + 𝐴𝐵′𝐶′ + 𝐵’𝐶𝐴 + 𝐵′𝐶𝐴′
→ 𝐴𝐵𝐶 + 𝐴𝐵𝐶′
+ 𝐴𝐵′
𝐶 + 𝐴𝐵′
𝐶′
+ 𝐵′
𝐶𝐴′
= 𝑚1 + 𝑚4 + 𝑚5 + 𝑚6 + 𝑚7
𝐹 𝐴, 𝐵, 𝐶 = σ(1,4,5,6,7)
𝒙 + 𝒙′ = 𝟏
𝒙 + 𝒙 = 𝒙

39. Canonical → [Product of Maxterms]
39
Express the Boolean function 𝐹 = 𝑥𝑦 + 𝑥’𝑧 as a product of
maxterms.
𝐹 = 𝑥𝑦 + 𝑥’𝑧 = 𝑥𝑦 + 𝑥′
𝑥𝑦 + 𝑧
→ 𝑦 + 𝑥′
𝑥 + 𝑥′
𝑦 + 𝑧 𝑥 + 𝑧
→ 𝑦 + 𝑥′ + 𝑧𝑧′ 𝑦 + 𝑧 + 𝑥𝑥′ 𝑥 + 𝑧 + 𝑦𝑦′
→ 𝑦 + 𝑥′
+ 𝑧′ 𝑦 + 𝑥′
+ 𝑧 𝑦 + 𝑧 + 𝑥′ 𝑦 + 𝑧 + 𝑥 𝑥 + 𝑧 + 𝑦′ 𝑥 + 𝑧 + 𝑦
→ 𝑦 + 𝑥′
+ 𝑧′ 𝑦 + 𝑧 + 𝑥′ 𝑦 + 𝑧 + 𝑥 𝑥 + 𝑧 + 𝑦′
= 𝑀0 + 𝑀2 + 𝑀4 + 𝑀5
𝐹 𝐴, 𝐵, 𝐶 = ς(0,2,4,5)
𝒙 + 𝒚𝒛 = (𝒙 + 𝒚)(𝒙 + 𝒛)
𝒙𝒙′ = 𝟎
𝒙𝒙 = 𝒙

40. Canonical → [
Conversion between Cononical Forms]
40
The complement of a function expressed as the sum of minterms equals the
sum of minterms missing from the original function.
1. 𝐹 𝐴, 𝐵, 𝐶 = σ 1,4,5,6,7 = 𝑚1 + 𝑚4 + 𝑚5 + 𝑚6 + 𝑚7
2. 𝐹′ 𝐴, 𝐵, 𝐶 = σ 0,2,3 = 𝑚0 + 𝑚2 + 𝑚3
3. 𝑓′ 𝐴, 𝐵, 𝐶 ′ = ς 0,2,3 = (𝑀0)(𝑀2)(𝑀3)

41. Canonical → [
Conversion between Cononical Forms]
41

42. Canonical → [
Conversion between Cononical Forms]
42
𝐹 = 𝑥𝑦 + 𝑥’𝑧
→ 𝑥𝑦 𝑧 + 𝑧′
+ 𝑥′
𝑧 𝑦 + 𝑦′
→ 𝑥𝑦𝑧 + 𝑥𝑦𝑧′ + 𝑥′𝑧𝑦 + 𝑥′𝑧𝑦′
= 𝑚7 + 𝑚6 + 𝑚3 + 𝑚1
𝐹 𝐴, 𝐵, 𝐶 = σ(1,3,6,7)
𝐹 = 𝑥𝑦 + 𝑥’𝑧
𝐹′ 𝐴, 𝐵, 𝐶 = σ(0,2,4,5)
𝑓′
𝐴, 𝐵, 𝐶 ′
= 𝑚0 + 𝑚2 + 𝑚4 + 𝑚5
′
𝐹 𝐴, 𝐵, 𝐶 = ෍(0,2,4,5)
𝐹 𝐴, 𝐵, 𝐶 = 𝑀0 𝑀2 𝑀4 𝑀5
→ 𝑦 + 𝑥′
+ 𝑧′ 𝑦 + 𝑧 + 𝑥′ 𝑦 + 𝑧 + 𝑥 𝑥 + 𝑧 + 𝑦′
𝒙 𝒚 𝒛
𝑴𝒊𝒏𝒕𝒆𝒓𝒎𝒔
𝑻𝒆𝒓𝒎 𝑫𝒆𝒔𝒊𝒈𝒏𝒂𝒕𝒊𝒐𝒏
𝟎 𝟎 𝟎 𝒙′
𝒚′
𝒛′ 𝒎𝟎
𝟎 𝟎 𝟏 𝒙′
𝒚′
𝒛 𝒎𝟏
𝟎 𝟏 𝟎 𝒙′
𝒚𝒛′ 𝒎𝟐
𝟎 𝟏 𝟏 𝒙′
𝒚𝒛 𝒎𝟑
𝟏 𝟎 𝟎 x𝒚′
𝒛′ 𝒎𝟒
𝟏 𝟎 𝟏 𝒙𝒚′
𝒛 𝒎𝟓
𝟏 𝟏 𝟎 𝒙𝒚𝒛′ 𝒎𝟔
𝟏 𝟏 𝟏 𝒙𝒚𝒛 𝒎𝟕

43. Canonical → [
Conversion between Cononical Forms]
43
𝐹 = 𝑥𝑦 + 𝑥’𝑧 = 𝑥𝑦 + 𝑥′
𝑥𝑦 + 𝑧
→ 𝑦 + 𝑥′
𝑥 + 𝑥′
𝑦 + 𝑧 𝑥 + 𝑧
→ 𝑦 + 𝑥′ + 𝑧𝑧′ 𝑦 + 𝑧 + 𝑥𝑥′ 𝑥 + 𝑧 + 𝑦𝑦′
→ 𝑦 + 𝑥′ + 𝑧′ 𝑦 + 𝑥′ + 𝑧 𝑦 + 𝑧 + 𝑥′ 𝑦 + 𝑧 + 𝑥 𝑥 + 𝑧 + 𝑦′ 𝑥 + 𝑧 + 𝑦
→ 𝑦 + 𝑥′
+ 𝑧′ 𝑦 + 𝑧 + 𝑥′ 𝑦 + 𝑧 + 𝑥 𝑥 + 𝑧 + 𝑦′
= 𝑀0 + 𝑀2 + 𝑀4 + 𝑀5
𝐹 𝐴, 𝐵, 𝐶 = ς(0,2,4,5)
𝐹 = 𝑥𝑦 + 𝑥’𝑧

44. Standard Forms
44
Another way to express Boolean functions is in standard form. In this
configuration, the terms that form the function may contain one, two, or
any number of literals.
There are two types of standard forms:
1. Sum of products → [ 𝑥𝑦 + 𝑥𝑧 + 𝑦𝑧]
2. Products of sums → [ 𝑥𝑦 + 𝑥𝑧 𝑦𝑧 ]

45. Standard Forms [Example]
45

46. Standard Forms [Example]
46

47. Question
.1
‫يب‬‫فل‬
‫فالب‬
( Flip Flop)
‫ست‬‫چی‬
,
‫از‬
‫کدام‬
Gate
‫های‬
‫ساخته‬
‫شده‬
‫و‬
‫به‬
‫چه‬
‫اهداف‬
‫از‬
‫ن‬‫آ‬
‫تفاده‬‫س‬‫ا‬
‫شود؟‬‫می‬
47