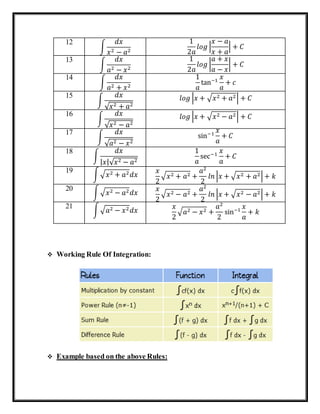
This document provides an introduction to definite integration and its applications. It defines indefinite integration as finding the integral or primitive function F(x) of a function f(x). Definite integration involves finding the area under a curve defined by a function f(x) over a specified interval. Standard formulae for integrating common functions like polynomials, trigonometric functions, and exponentials are provided. Methods for integrating functions using substitution and integration by parts are described. Examples of applying these techniques to evaluate definite integrals are also given.

1. Class: B.Sc CS.
Subject: Discrete Mathematics
Unit-2
RAI UNIVERSITY, AHMEDABAD

2. UNIT- 2: Definite Integration and it’s Application
 Introduction:
 In Mathematics, whenever possible, we think of an Oppositeor
inverse Process ofa given Process.Forexample, Subtraction is
inverse process ofaddition and division is inverse process of
multiplication. Similarly, integration is inverse process of
differentiation.
 Integration can be used to find areas, volumes, central points and
many useful things. But it is easiest to start with finding the area
under the curve of a function like this:
What is the area under y = f(x)?
 There are two types of integration:
1. Indefinite Integration.
2. Definite Integration.
 Definition : Indefinite Integration
If 𝑓(𝑥) is the derivative of a differentiable function 𝐹(𝑥) with respect
to 𝑥 in the interval𝐼 ⊂ 𝑅.
i.e. if
𝑑
𝑑𝑥
𝐹( 𝑥) = 𝑓( 𝑥), 𝑥 ∈ 𝐼
then 𝐹(𝑥) is called integral or primitive of 𝑓(𝑥) with respectto𝑥.
 Symbolically it is written as
∫ 𝑓( 𝑥) 𝑑𝑥 = 𝐹(𝑥)
 Readas “𝐹( 𝑥) is the integral of 𝑓( 𝑥) with respect to 𝑥.

3.  Here the sign ′∫ ′ denotes the Process ofintegration and it is called
sign of integration.
 The function 𝑓( 𝑥) whose integration is to be obtained is called the
integrand.
 The Process offinding integrals of given functions is called definite
integration.
 A function whose integration can be obtained is called an integrable
function.
Notation:
 After the Integral Symbol we put the function we want to find the integral of
(called the Integrand), and then finish with 𝒅𝒙 go in the 𝑥 direction (and
approachzero in width).
 And here is how we write the answer:
 We wrote the answer as 𝑥2
but why + C?

4.  It is the "Constantof Integration". It is there becauseof all the functions
whose derivative is 𝟐𝒙:
So when we reverse the
operation (to find the integral) we only know 2x, but there could have been a
constant of any value.
 So we wrap up the idea by just writing + C at the end.
 Standard Formulae Of Integration:
Sr. No. Function Integration
1
∫ 𝑥 𝑛
𝑑𝑥
𝑥 𝑛+1
𝑛 + 1
+ 𝐶
2
∫1 𝑑𝑥
𝑥 + 𝐶
3
∫
1
𝑥
𝑑𝑥
ln| 𝑥| + 𝐶
4
∫ 𝑐𝑜𝑠𝑥𝑑𝑥
sin 𝑥 + 𝐶
5
∫ 𝑠𝑖𝑛𝑥𝑑𝑥
−𝑐𝑜𝑠𝑥 + 𝐶
6
∫ 𝑠𝑒𝑐2
𝑥 𝑑𝑥
tan 𝑥 + 𝐶
7
∫ 𝑐𝑜𝑠𝑒𝑐2
𝑥 𝑑𝑥
−cot 𝑥 + 𝐶
8
∫sec 𝑥 tan 𝑥 𝑑𝑥
sec 𝑥 + 𝐶
9
∫ 𝑐𝑜𝑠𝑒𝑐𝑥 cot 𝑥𝑑𝑥
−𝑐𝑜𝑠𝑒𝑐 𝑥 + 𝐶
10
∫ 𝑒 𝑥
𝑑𝑥
𝑒 𝑥
+ 𝐶
11
∫ 𝑎 𝑥
𝑑𝑥
𝑎 𝑥
ln 𝑎
+ 𝐶

5. 12
∫
𝑑𝑥
𝑥2 − 𝑎2
1
2𝑎
𝑙𝑜𝑔 |
𝑥 − 𝑎
𝑥 + 𝑎
| + 𝐶
13
∫
𝑑𝑥
𝑎2 − 𝑥2
1
2𝑎
𝑙𝑜𝑔 |
𝑎 + 𝑥
𝑎 − 𝑥
| + 𝐶
14
∫
𝑑𝑥
𝑎2 + 𝑥2
1
𝑎
tan−1
𝑥
𝑎
+ 𝑐
15
∫
𝑑𝑥
√ 𝑥2 + 𝑎2
𝑙𝑜𝑔 |𝑥 + √ 𝑥2 + 𝑎2| + 𝐶
16
∫
𝑑𝑥
√ 𝑥2 − 𝑎2
𝑙𝑜𝑔 |𝑥 + √ 𝑥2 − 𝑎2| + 𝐶
17
∫
𝑑𝑥
√ 𝑎2 − 𝑥2
sin−1
𝑥
𝑎
+ 𝐶
18
∫
𝑑𝑥
| 𝑥|√ 𝑥2 − 𝑎2
1
𝑎
sec−1
𝑥
𝑎
+ 𝐶
19
∫√ 𝑥2 + 𝑎2 𝑑𝑥
𝑥
2
√ 𝑥2 + 𝑎2 +
𝑎2
2
𝑙𝑛 |𝑥 + √ 𝑥2 + 𝑎2| + 𝑘
20
∫√ 𝑥2 − 𝑎2 𝑑𝑥
𝑥
2
√ 𝑥2 − 𝑎2 +
𝑎2
2
𝑙𝑛 |𝑥 + √ 𝑥2 − 𝑎2| + 𝑘
21
∫√ 𝑎2 − 𝑥2 𝑑𝑥
𝑥
2
√ 𝑎2 − 𝑥2 +
𝑎2
2
sin−1
𝑥
𝑎
+ 𝑘
 Working Rule Of Integration:
 Example based on the above Rules:

6.  Example-1. Solve the integral ∫ 𝒙 𝟓
𝒅𝒙 .
Solution: ∫ 𝑥5
𝑑𝑥 =
𝑥5+1
5+1
+ 𝑘 =
1
6
𝑥6
+ 𝑘
 Example-2. Solve the integral ∫ 𝒙
𝟑
𝟐 𝒅𝒙 .
Solution: ∫ 𝑥
3
2 𝑑𝑥 =
𝑥
3
2
+1
3
2
+1
+ 𝑘 =
𝑥
5
2
5
2
+ 𝑘 =
2
5
𝑥
5
2 + 𝑘
 Example-3. Solve the integral ∫ (𝟒𝒄𝒐𝒔𝒙 − 𝟑𝒆 𝒙
+
𝟐
√ 𝟏−𝒙 𝟐
) 𝒅𝒙 .
Solution: ∫ (4𝑐𝑜𝑠𝑥 − 3𝑒 𝑥
+
2
√1−𝑥2
) 𝑑𝑥
= 4 ∫cos 𝑥 𝑑𝑥 − 3 ∫ 𝑒 𝑥
𝑑𝑥 + 2 ∫
𝑑𝑥
√1−𝑥2
= 4 𝑠𝑖𝑛𝑥 − 3𝑒 𝑥
+ 2sin−1
𝑥 + 𝑘

7.  Methods of integration
1. Integration by substitution—
If integrand is not in the standard form and can be transformed to integral form
by a suitable substitution then such process ofintegration is called as
integration by substitution.
Take these steps to evaluate the integral ∫ 𝑓{ 𝑔( 𝑥)} 𝑔′( 𝑥) 𝑑𝑥, where 𝑓 and 𝑔′are
contineous function—
Step 1: Substitute 𝑧 = 𝑔(𝑥) and 𝑑𝑧 = 𝑔′( 𝑥) 𝑑𝑥 to obtain the integral ∫ 𝑓( 𝑧) 𝑑𝑧.
Step 2: Integrate with respectto .
Step 3: Replace 𝑧 by 𝑔(𝑥) in the result.
 Example—Solve the following integral ∫
𝟏
𝒄𝒐𝒔 𝟐 𝟐𝜽
𝒅𝜽 .
Solution: ∫
1
𝑐𝑜𝑠22𝜃
𝑑𝜃
= ∫ 𝑠𝑒𝑐2
2𝜃𝑑𝜃
= ∫ 𝑠𝑒𝑐2
𝑧.
1
2
𝑑𝑧 [
𝑧 = 2𝜃
⟹ 𝑑𝑧 = 2𝑑𝜃
⟹ 𝑑𝜃 =
1
2
𝑑𝑧
]
=
1
2
∫ 𝑠𝑒𝑐2
𝑧. 𝑑𝑧
=
1
2
𝑡𝑎𝑛 𝑧+ 𝑘
=
1
2
𝑡𝑎𝑛 2𝜃 + 𝑘
Example— Evaluate ∫( 𝟐𝒙 + 𝟑) 𝟕
𝒅𝒙 .
Solution— ∫(2𝑥 + 3)7
𝑑𝑥
=∫ 𝑧7 1
2
𝑑𝑧 Let 2𝑥 + 3 = 𝑧
=
1
2
∫ 𝑧7
𝑑𝑧 2𝑑𝑥 = 𝑑𝑧

8. =
𝑧8
16
+ 𝑘 𝑑𝑥 =
1
2
𝑑𝑧
=
(2𝑥+3)8
16
+ 𝑘
Example— Integrate ∫
𝒆 𝒙
𝒆 𝟐𝒙+𝟗
𝒅𝒙 .
Solution— ∫
𝑒 𝑥
𝑒2𝑥+9
𝑑𝑥
=∫
𝑧
𝑧2+9
1
𝑧
𝑑𝑧 Let 𝑒 𝑥
= 𝑧
= ∫
1
𝑧2+9
𝑑𝑧 𝑒 𝑥
𝑑𝑥 = 𝑑𝑧
= ∫
1
𝑧2+(3)2
𝑑𝑧 𝑑𝑥 =
1
𝑒 𝑥
𝑑𝑧
=
1
3
tan−1
(
𝑧
3
) + 𝑘 𝑑𝑥 =
1
𝑧
𝑑𝑧
=
1
3
tan−1
(
𝑒 𝑥
3
) + 𝑘
2. Integration by method of parts—
If 𝑢 and 𝑣 are functions of 𝑥 then the integral of productof these functions is
given by—
∫ 𝑢 𝑣 𝑑𝑥 =(𝑣 ∫ 𝑢𝑑𝑥)− ∫
𝑑𝑣
𝑑𝑥
(∫ 𝑢𝑑𝑥)𝑑𝑥
This rule is called as ‘integration by method of parts’.
The choice of first and second integral is given by—
I— Inverse
L—Logarithmic
A—Algebraic
T—Trigonometric
E—Exponential

9. The term appearing first in this series have to take first integral (u).
 Example—Integrate ∫ 𝒙 𝐜𝐨𝐬 𝒙 𝒅𝒙 .
Solution: ∫ 𝑥 cos 𝑥 𝑑𝑥
=( 𝑥 ∫ cos 𝑥 𝑑𝑥) − ∫
𝑑𝑥
𝑑𝑥
(∫cos 𝑥 𝑑𝑥) 𝑑𝑥
= 𝑥𝑠𝑖𝑛 𝑥 − ∫sin 𝑥𝑑𝑥 = 𝑥 sin 𝑥 + cos 𝑥 + 𝑘
 Integration of terms involving multiple trigonometric functions—
1. 𝑠𝑖𝑛 𝑚𝑥 cos 𝑛𝑥 =
1
2
. 2 sin 𝑚𝑥 cos 𝑛𝑥 =
1
2
[sin( 𝑚 + 𝑛) 𝑥 + cos( 𝑚 − 𝑛) 𝑥]
2. sin 𝑚𝑥 sin 𝑛𝑥 =
1
2
[cos( 𝑚 − 𝑛) 𝑥 − cos( 𝑚 + 𝑛) 𝑥]
3. cos 𝑚𝑥 cos 𝑛𝑥 =
1
2
[cos( 𝑚 − 𝑛) 𝑥 − cos( 𝑚 + 𝑛) 𝑥]
3. sin2
𝑥 =
1
2
(1 − cos 2𝑥)
4. cos2
𝑥 =
1
2
(1 + 𝑐𝑜𝑠 2𝑥)
5. sin3
𝑥 =
1
4
(3sin 𝑥 − sin 3𝑥)
6. cos3
𝑥 =
1
4
(3cos 𝑥 + cos 3𝑥)
 Example-1. Evaluate ∫ 𝐬𝐢𝐧 𝟑𝒙 𝐜𝐨𝐬 𝟐𝒙 𝒅𝒙 .
Solution: ∫ sin 3𝑥 cos 2𝑥 𝑑𝑥
=
1
2
∫ 2 sin 3𝑥cos 2𝑥 𝑑𝑥
=
1
2
∫(sin5𝑥 + sin 𝑥) 𝑑𝑥
=
1
2
(−
1
5
𝑐𝑜𝑠 5𝑥 − 𝑐𝑜𝑠 𝑥)+ 𝑘

10. =
−1
10
(cos 5𝑥 + 5 cos 𝑥) + 𝑘
 Example-2. Integrate ∫ 𝒔𝒊𝒏 𝟑
𝒙 𝒅𝒙 .
Solution: ∫ sin3
𝑥 𝑑𝑥
=
1
4
∫(3sin 𝑥 − sin 3𝑥) 𝑑𝑥
=
1
4
(−3cos 𝑥 +
1
3
cos 3𝑥)+ 𝑘
=
−3
4
cos 𝑥 +
1
12
cos 3𝑥 + 𝑘
2. Definite integration
Definition— If 𝑓(𝑥) is continuous in the interval [𝑎, 𝑏] and 𝐹(𝑥) is an
antiderivative of 𝑓(𝑥), then
Elementary properties of definite integral—
1. ∫ 𝑓( 𝑥) 𝑑𝑥 = −
𝑏
𝑎
∫ 𝑓( 𝑥) 𝑑𝑥
𝑎
𝑏
2. ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
= ∫ 𝑓( 𝑦) 𝑑𝑦
𝑏
𝑎
= ∫ 𝑓( 𝑧) 𝑑𝑧
𝑏
𝑎
3. ∫ 𝑓( 𝑥) 𝑑𝑥 = 0
𝑐
𝑐
∫ 𝒇( 𝒙) 𝒅𝒙 = 𝑭( 𝒃) − 𝑭(𝒂)
𝒃
𝒂

11. 4. ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
= ∫ 𝑓( 𝑥) 𝑑𝑥
𝛼
𝑎
+ ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝛼
, 𝑎 < 𝛼 < 𝑏
5. ∫ 𝑓( 𝑎 + 𝑏 − 𝑥) 𝑑𝑥 = ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
𝑏
𝑎
6. ∫ 𝑓( 𝑎 − 𝑥) 𝑑𝑥 = ∫ 𝑓( 𝑥) 𝑑𝑥
𝑎
0
𝑎
0
7. ∫ 𝑓( 𝑥) 𝑑𝑥 = {
2 ∫ 𝑓( 𝑥) 𝑑𝑥 if 𝑓 is even function
𝑎
0
0 if 𝑓 is odd function
𝑎
−𝑎
8. ∫ 𝑓( 𝑥) 𝑑𝑥 =
2𝑎
0
{
2 ∫ 𝑓( 𝑥) 𝑑𝑥 if 𝑓 (2𝑎 − 𝑥) = 𝑓(𝑥)
𝑎
0
0 if 𝑓(2𝑎 − 𝑥) = −𝑓(𝑥)
5.3 Standard properties of definite integral—
1. If 𝑓(𝑥) ≥ 0 is defined and continuous on[𝑎, 𝑏], then ∫ 𝑓( 𝑥) 𝑑𝑥 ≥ 0
𝑏
𝑎
2. If 𝑓(𝑥) ≤ 0 is defined and continuous on[𝑎, 𝑏], then ∫ 𝑓( 𝑥) 𝑑𝑥 ≤ 0
𝑏
𝑎
3. If 𝑓(𝑥) ≤ 𝑔(𝑥) is defined and continuous on[𝑎, 𝑏],
then ∫ 𝑓( 𝑥) 𝑑𝑥 ≤ ∫ 𝑔( 𝑥) 𝑑𝑥
𝑏
𝑎
𝑏
𝑎
4. If 𝑓(𝑥) and 𝑔(𝑥) be two functions defined and continuous on [a, b] then—
(∫ 𝑓( 𝑥) 𝑔( 𝑥) 𝑑𝑥
𝑏
𝑎
)
2
≤ ∫ (𝑓( 𝑥))
2
𝑑𝑥 ∫ (𝑔( 𝑥))
2
𝑑𝑥
𝑏
𝑎
𝑏
𝑎
5. The mean value theorem—
Statement— If 𝑓(𝑥) is continuous on [𝑎, 𝑏], then at least one value of 𝑥 = 𝑐
in (𝑎, 𝑏)
such that—
𝑓( 𝑐) =
1
𝑏−𝑎
∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎

12. Where 𝑓( 𝑐) is called as average or mean value of 𝑓( 𝑥) on [ 𝑎, 𝑏].
 Example-1 Integrate ∫ 𝒙 𝟑
𝒅𝒙
𝟐
𝟏
.
Solution:∫ 𝑥3
𝑑𝑥
2
1
= |
𝑥4
4
|
1
2
=
24
4
−
14
4
=
15
4
 Example-2 Integrate ∫ 𝒔𝒊𝒏 𝒙 𝒅𝒙
𝝅
𝟐
𝟎
Solution:∫ 𝑠𝑖𝑛 𝑥 𝑑𝑥
𝜋
2
0
= |−cos 𝑥|0
𝜋
2
= (−cos
𝜋
2
) —cos 0
= 0 − (−1) = 1
 Example-3 Integrate ∫ 𝒍𝒐𝒈𝒙 𝒅𝒙
𝒆
𝟏
Solution: ∫ 𝑙𝑜𝑔𝑥 𝑑𝑥
𝑒
1
= [𝑙𝑜𝑔𝑥∫ 𝑑𝑥 − ∫
𝑑(𝑙𝑜𝑔𝑥)
𝑑𝑥
(∫ 𝑑𝑥) 𝑑𝑥]
1
𝑒
= [𝑥𝑙𝑜𝑔𝑥 − ∫
1
𝑥
𝑥 𝑑𝑥]
1
𝑒
= [ 𝑥𝑙𝑜𝑔𝑥 − ∫ 𝑑𝑥]1
𝑒
= [ 𝑥𝑙𝑜𝑔𝑥 − 𝑥]1
𝑒
= ( 𝑒 𝑙𝑜𝑔𝑒 − 𝑒) − ( 𝑙𝑜𝑔1− 1)
= ( 𝑒 − 𝑒) + 1 = 1
Example-4 Evaluate ∫ 𝐬𝐢𝐧 𝟑𝒙 𝐜𝐨𝐬 𝟐𝒙 𝒅𝒙
𝝅
𝟐
𝟎

13. Solution:∫ 𝑠𝑖𝑛 3𝑥 𝑐𝑜𝑠 2𝑥𝑑𝑥
𝜋
2
0
=
1
2
∫ 2 𝑠𝑖𝑛 3𝑥 𝑐𝑜𝑠 2𝑥 𝑑𝑥
𝜋
2
0
=
1
2
∫ ( 𝑠𝑖𝑛5𝑥 + 𝑠𝑖𝑛 𝑥) 𝑑𝑥
𝜋
2
0
=
1
2
(−
1
5
𝑐𝑜𝑠 5𝑥 − 𝑐𝑜𝑠 𝑥)
0
𝜋
2
=
1
2
[(−
1
5
𝑐𝑜𝑠 5
𝜋
2
− 𝑐𝑜𝑠
𝜋
2
) − (−
1
5
𝑐𝑜𝑠 0 − 𝑐𝑜𝑠 0)]
=
1
2
[(0 − 0) − (−
1
5
− 1)]
=
3
5
 Example based on the PartialFraction:
 Example-1. Evaluate ∫
(𝟐𝒙−𝟑)
(𝒙 − 𝟐)(𝒙 + 𝟑)
𝒅𝒙
Solution: Observe that the factors in the denominator are ( 𝑥 − 2) and (𝑥 + 3)
so, we can write

(2𝑥−3)
(𝑥 − 2)(𝑥 + 3)
=
𝐴
(𝑥 − 2)
+
𝐵
(𝑥 + 3)
, where A and B are numbers.
 Now, multiplying both sides by the common denominator (𝑥 − 2)(𝑥 + 3)
2𝑥 − 3 = 𝐴(𝑥 − 2) + 𝐵(𝑥 + 3)
2𝑥 − 3 = ( 𝐴 + 𝐵) 𝑥 − (2𝐴 − 3𝐵)
 By comparing L.H.S & R.H.S—
 𝐴 + 𝐵 = 2 …eqn (1)
 2𝐴 − 3𝐵 = 3 …eqn (2)
 Now, solving eqn (1) & eqn (2) –
𝐴 =
9
5
and 𝐵 =
1
5
 Hence, putting these results together we have

14. 
(2𝑥−3)
(𝑥 − 2)(𝑥 + 3)
=
9
5
(𝑥 − 2)
+
1
5
(𝑥 + 3)
 ∫
(2𝑥−3)
(𝑥 − 2)(𝑥 + 3)
𝑑𝑥 =
9
5
∫
1
𝑥−2
𝑑𝑥 +
1
5
∫
1
𝑥+3
𝑑𝑥
5
4
5
4
5
4
 ∫
(2𝑥−3)
(𝑥 − 2)(𝑥 + 3)
𝑑𝑥 =
9
5
𝑙𝑜𝑔 ( 𝑥 − 2)4
5
+
1
5
𝑙𝑜𝑔( 𝑥 + 3)4
5
 ∫
(2𝑥−3)
( 𝑥 – 2)( 𝑥 + 3)
𝑑𝑥 =
9
5
[log(5 − 2) − log(4 − 2)]
+
1
5
[log(5 + 3) − log(4 + 3)].
 ∫
(2𝑥−3)
( 𝑥 – 2)( 𝑥 + 3)
𝑑𝑥 =
9
5
[log(
3
2
)] +
1
5
[log(
8
7
) ]
 Example -1. Evaluate ∫
𝒔𝒆𝒄𝒙
𝒔𝒆𝒄𝒙+𝒄𝒐𝒔𝒆𝒄𝒙
𝝅
𝟐
𝟎
𝒅𝒙
Solution:
 I = ∫
𝑠𝑒𝑐𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑒𝑐𝑥
𝜋
2
0
𝑑𝑥
 𝐼 = ∫
𝑠𝑒𝑐(
𝜋
2
−𝑥)
𝑠𝑒𝑐(
𝜋
2
−𝑥)+𝑐𝑜𝑠𝑒𝑐(
𝜋
2
−𝑥)
𝜋
2
0
𝑑𝑥 [∫ 𝑓( 𝑥) 𝑑𝑥 = ∫ 𝑓( 𝑎 − 𝑥) 𝑑𝑥
𝑎
0
𝑎
0
]
 𝐼 = ∫
𝑐𝑜𝑠𝑒𝑐𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑒𝑐𝑥
𝜋
2
0
𝑑𝑥
 Adding (1) and (2) we get
 2𝐼 = ∫
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑒𝑐𝑥
𝑠𝑒𝑐𝑥+𝑐𝑜𝑠𝑒𝑐𝑥
𝜋
2
0
𝑑𝑥
 2𝐼 = ∫ 1𝑑𝑥
𝜋
2
0
 2𝐼 = [ 𝑥]0
𝜋
2
 2𝐼 =
𝜋
2
 𝑖. 𝑒. 𝐼 =
𝜋
4
 Example: Evaluate ∫
𝒙𝒔𝒊𝒏𝒙
𝟏+𝒔𝒊𝒏𝒙
𝝅
𝟎
𝒅𝒙

15.  Solution: 𝐼 = ∫
𝑥𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥
 𝐼 = ∫
( 𝜋−𝑥) 𝑠𝑖𝑛(𝜋−𝑥)
1+𝑠𝑖𝑛(𝜋−𝑥)
𝜋
0
𝑑𝑥
 𝐼 = ∫
(𝜋−𝑥)𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥
 𝐼 = ∫
𝜋𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥 − ∫
𝑥𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥
 𝐼 = 𝜋 ∫
𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥 − 𝐼
 ∴ 2𝐼 = 𝜋 ∫
𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
𝑑𝑥
 2𝐼 = 𝜋 ∫ [
𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
𝜋
0
×
1−𝑠𝑖𝑛𝑥
1+𝑠𝑖𝑛𝑥
]𝑑𝑥
 2𝐼 = 𝜋 ∫
𝑠𝑖𝑛𝑥(1−𝑠𝑖𝑛𝑥)
1−𝑠𝑖𝑛2 𝑥
𝜋
0
𝑑𝑥
 2𝐼 = 𝜋 ∫
𝑠𝑖𝑛𝑥−𝑠𝑖𝑛2 𝑥
𝑐𝑜𝑠2 𝑥
𝜋
0
𝑑𝑥
 2𝐼 = 𝜋 ∫ [
𝑠𝑖𝑛𝑥
𝑐𝑜𝑠2 𝑥
𝜋
0
−
𝑠𝑖𝑛2 𝑥
𝑐𝑜𝑠2 𝑥
]𝑑𝑥
 2𝐼 = 𝜋 ∫ [
1
𝑐𝑜𝑠𝑥
.
𝜋
0
𝑠𝑖𝑛𝑥
𝑐𝑜𝑠𝑥
− (
𝑠𝑖𝑛𝑥
𝑐𝑜𝑠𝑥
)
2
]𝑑𝑥
 2𝐼 = 𝜋 ∫ [ 𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 − 𝑡𝑎𝑛2
𝑥] 𝑑𝑥
𝜋
0
 2𝐼 = 𝜋 ∫ [𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 − (sec2
𝑥 − 1)]𝑑𝑥
𝜋
0
 2𝐼 = 𝜋 ∫ [𝑠𝑒𝑐𝑥𝑡𝑎𝑛𝑥 − sec2
𝑥 + 1]𝑑𝑥
𝜋
0
 2𝐼 = 𝜋[𝑠𝑒𝑐𝑥 − 𝑡𝑎𝑛𝑥 + 𝑥]0
𝜋
 2𝐼 = 𝜋[( 𝑠𝑒𝑐 𝜋 − 𝑡𝑎𝑛 𝜋 + 𝜋) − ( 𝑠𝑒𝑐0 − 𝑡𝑎𝑛0+ 0)]
 2𝐼 = 𝜋[(−1 − 0 + 𝜋) − (1 − 0 + 0)]
 ∴ 2𝐼 = 𝜋( 𝜋 − 2)
 ∴ 𝐼 =
𝜋
2
( 𝜋 − 2)
 Application of Definite Integration:

16.  We shall now discuss some geometrical applications of definite integrals
which are useful in engineering problems. We shall discuss the use of
definite integrals for finding area and volume.
(A) Area:
The Area bounded by a curve 𝑦 = 𝑓( 𝑥), the X-axis and the ordinates
𝑥 = 𝑎 and 𝑥 = 𝑏 is given by the definite integral 𝐴 = ∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
 The area is obtained by dividing the given figure in small parallel strips
with equal bases and taking the sum of the areas of the strips when the
number of strips is very large.
 If a function 𝑦 = 𝑓(𝑥) is continuous on the interval [a, b] then the area
bounded by the curve 𝑦 = 𝑓( 𝑥), the X-axis and the lines 𝑥 = 𝑎 and 𝑥 =
𝑏 is given by 𝐴 = |∫ 𝑓( 𝑥) 𝑑𝑥
𝑏
𝑎
|
 If a function 𝑥 = 𝑔(𝑦) is continuous on the interval [c, d], then the area
bounded by the curve 𝑥 = 𝑔( 𝑦), the Y-axis and the lines 𝑦 = 𝑐 and 𝑦 =
𝑑 is given by 𝐴 = |∫ 𝑔( 𝑦) 𝑑𝑦
𝑑
𝑐
|
Area betweentwo curves:

17. (1). If two curves 𝑦 = 𝑓1 (𝑥) and 𝑦 = 𝑓2 (𝑥) intersect only in two points
𝑥 = 𝑎 and 𝑥 = 𝑏 then the area bounded by the two curves is given by
𝐴 = |∫ [𝑓1
𝑏
𝑎
( 𝑥) − 𝑓2(𝑥)]𝑑𝑥|
(2). Similarly, if two curves 𝑥 = 𝑔1(𝑦) and 𝑥 = 𝑔2(𝑦) intersect in the points
𝑦 = 𝑐 and 𝑦 = 𝑑, then the area bounded by the two curves is given by
𝐴 = |∫ [𝑔1
𝑑
𝑐
( 𝑦) − 𝑔2(𝑦)]𝑑𝑦|
 Example-1. Find the area of the Standard circle 𝒙 𝟐
+ 𝒚 𝟐
= 𝒂 𝟐
, (𝒂 > 0).
Solution: The equation of the circle is 𝑥2
+ 𝑦2
= 𝑎2
∴ The centre of the circle is O(0,0) and its radius is 𝑎.
The circle is Symmetric with respect to both the axes in (𝑎, 0),
(0, 𝑎), (−𝑎,0) 𝑎𝑛𝑑 (0,−𝑎).
As the circle is symmetric with respectto the Origin, its total area is four
times its area in the first quadrant. For this the limits are 𝑥 = 0 and 𝑥 = 𝑎.
Now 𝑦2
= 𝑎2
− 𝑥2
∴ 𝑦 = √ 𝑎2 − 𝑥2
If 𝐴1 is the area of region in the first quadrant, then

18. 𝐴1=∫ 𝑦𝑑𝑥
𝑎
0
= ∫ √ 𝑎2 − 𝑥2𝑎
0
𝑑𝑥
𝐴1 = [
𝑥
2
√ 𝑎2 − 𝑥2 +
𝑎2
2
sin−1 𝑥
𝑎
]
0
𝑎
.
𝐴1 = [
𝑎
2
√ 𝑎2 − 𝑎2 +
𝑎2
2
sin−1 𝑎
𝑎
]
0
𝑎
− [0 + 0].
𝐴1 =
𝑎2
2
sin−1
1.
𝐴1 =
𝑎2
2
.
𝜋
2
=
𝜋𝑎2
4
.
∴ Total area of the circle = 𝐴 = 4𝐴1 = 4(
𝜋𝑎2
4
) = 𝜋𝑎2
 Example-2: Determine Area of the region enclosedby 𝒚 = 𝒙 𝟐
and 𝒚 = √ 𝒙.
Solution:First of all, just what we mean by “area enclosed by”.
 This means that the region we’re interested in must have one of the two
curves on every boundary of the region.
 So, here is a graph of the two functions with the enclosed region shaded.
 The limits of integration for this will be the intersection points of the two
curves. In this caseit’s pretty easy to see that they will intersect at 𝑥 =
0 and 𝑥 = 1 so these are the limits of integration.
 𝐴 = ∫ [ 𝑓1( 𝑥) − 𝑓2 ( 𝑥)] 𝑑𝑥
𝑏
𝑎
 𝐴 = ∫ (√ 𝑥
1
0
− 𝑥2
)𝑑𝑥

19.  𝐴 = ∫ √ 𝑥
1
0
𝑑𝑥 − ∫ 𝑥2
𝑑𝑥
1
0
 𝐴 =
2
3
[𝑥
3
2]
0
1
−
1
3
[ 𝑥3]0
1
 𝐴 =
2
3
[1 − 0] −
1
3
[1 − 0]
 𝐴 =
2
3
−
1
3
 𝐴 =
1
3
(B). Volume of a Solid revolution:
The Solids generated by revolving a plane area about a fixed line not
intersecting the plane area are called solids of revolution.
 Let 𝑦 = 𝑓(𝑥) be a continuous function on [a, b] and let 𝑓(𝑥) > 0. The
volume of the solid generated by the revolution of the area bounded by the
curve 𝑦 = 𝑓( 𝑥), the X-axis and the lines 𝑥 = 𝑎 and 𝑥 = 𝑏 about the X-axis
Is given by
𝑉 = 𝜋 ∫ 𝑦2
𝑑𝑥 = 𝜋∫ [ 𝑓( 𝑥)]2
𝑑𝑥
𝑏
𝑎
𝑏
𝑎

20.  Let 𝑥 = 𝑔(𝑦) be a continuous function on [a, b] and let 𝑔(𝑦) > 0. The
volume of the solid generated by the revolution of the area bounded by the
curve 𝑥 = 𝑔( 𝑦), the Y-axis and the lines 𝑦 = 𝑐 and 𝑦 = 𝑑 about the Y-axis
Is given by
𝑉 = 𝜋∫ 𝑥2
𝑑𝑦 = 𝜋 ∫ [ 𝑔( 𝑦)]2
𝑑𝑦
𝑑
𝑐
𝑑
𝑐
Volume betweentwo curves:
(1). If two different curves 𝑦 = 𝑓1(𝑥) and 𝑦 = 𝑓2 (𝑥) intersect in two
distinct points whose 𝑥 −coordinates are 𝑎 and 𝑏, then the volume of the
solid of revolution Obtained by revolving the area bounded by the two
curves about the X-axis is given by
𝑉 = 𝜋 ∫ [{ 𝑓1 ( 𝑥)}2
− { 𝑓2 ( 𝑥)}2] 𝑑𝑥
𝑏
𝑎
(2). Similarly, for two different curves 𝑥 = 𝑔1(𝑦) and 𝑥 = 𝑔2( 𝑦), the
volume of the solid generated is given by
𝑉 = 𝜋 ∫ [{ 𝑔1( 𝑦)}2
− { 𝑔2( 𝑦)}2] 𝑑𝑦
𝑑
𝑐
 Example-1. Find the volume of the sphere having radius 𝒂.
Solution: The sphere is symmetrical about X-,Y- and Z- axes. Also it is
Symmetrical with respect to the origin. If we rotate the semi-circle given by
the equation 𝑥2
+ 𝑦2
= 𝑎2
about the X-axis, we get the sphere with radius
𝑎. The limits are – 𝑎 to 𝑎.

21.  Now 𝑥2
+ 𝑦2
= 𝑎2
⟺ 𝑦2
= 𝑎2
− 𝑥2
 The required volume is
𝑉 = 𝜋∫ 𝑦2
𝑑𝑥
𝑎
−𝑎
 𝑉 = 𝜋∫ ( 𝑎2
− 𝑥2) 𝑑𝑥
𝑎
−𝑎
 𝑉 = 2𝜋∫ ( 𝑎2
− 𝑥2) 𝑑𝑥
𝑎
0
 𝑉 = 2𝜋[𝑎2
𝑥 −
𝑥3
3
]
0
𝑎
 𝑉 = 2𝜋[𝑎3
−
𝑎3
3
]
 𝑉 = 2𝜋[
2𝑎3
3
]
 𝑉 =
4
3
𝜋𝑎3
 ∴ Volume of the sphere =
4
3
𝜋𝑎3
 Example-2. Find the volume of the solid generatedby revolving the
regionbounded by the graph of 𝒚 = 𝒙, 𝒚 = 𝟎, 𝒙 = 𝟎 and𝒙 = 𝟐. At
the solid

22. Solution: we shall now use definite integrals to find the volume defined
above. If we let 𝑓(𝑥) = 𝑥 according to 1 above, the volume is given by the
definite integral.
 Volume = 𝝅 ∫ 𝒚 𝟐
𝒅𝒙
𝒃
𝒂
 𝑉 = ∫ 𝜋𝑥2
𝑑𝑥
2
0
 𝑉 = 𝜋∫ 𝑥2
𝑑𝑥
2
0
 𝑉 = 𝜋[
𝑥3
3
]
0
2
 𝑉 = 𝜋[
8
3
− 0]
 𝑉 =
8𝜋
3
 Example-3.Obtain the volumes of the solids of revolution obtained by
revolving the ellipse
𝒙 𝟐
𝒂 𝟐
+
𝒚 𝟐
𝒃 𝟐
= 𝟏 about (i) the X-axis (ii) the Y-axis
Solution: The given ellipse intersects the X-axis in the points is (a, 0) and
(-a, 0) and the Y-axis in the points is (0, b) and (0, -b).
 The centre of the ellipse is O(0,0).
 Now
𝑥2
𝑎2
+
𝑦2
𝑏2
= 1
 𝑦2
= 𝑏2
(1 −
𝑥2
𝑎2
) and 𝑥2
= 𝑎2
(1 −
𝑦2
𝑏2
)
 Rotationabout the X-axis: The volume of the solid generated by revolving
the given ellipse about the X-axis is given by
 𝑉 = 𝜋∫ 𝑦2
𝑑𝑥
𝑎
−𝑎
 𝑉 = 2𝜋∫ 𝑦2
𝑑𝑥
𝑎
0
(∴ 𝑦2
is even function)

23.  𝑉 = 2𝜋∫ 𝑏2
(1 −
𝑥2
𝑎2
) 𝑑𝑥
𝑎
0
 𝑉 = 2𝜋𝑏2
∫ (1 −
𝑥2
𝑎2
) 𝑑𝑥
𝑎
0
 𝑉 =
2𝜋𝑏2
𝑎2 ∫ ( 𝑎2
− 𝑥2) 𝑑𝑥
𝑎
0
 𝑉 =
2𝜋𝑏2
𝑎2
[𝑎2
𝑥 −
𝑥3
3
]
0
𝑎
 𝑉 =
2𝜋𝑏2
𝑎2
[𝑎3
−
𝑎3
3
]
 𝑉 =
2𝜋𝑏2
𝑎2
.
2𝑎3
3
 𝑉 =
4
3
𝜋𝑎𝑏2
 Rotationabout the Y-axis: The volume of the solid generated by revolving
the given ellipse about the Y-axis is given by
 𝑉′
= 𝜋∫ 𝑥2
𝑑𝑦
𝑏
−𝑏
 𝑉′
= 2𝜋∫
𝑎2
𝑏2
( 𝑏2
− 𝑦2) 𝑑𝑦
𝑏
0
 𝑉′
=
2𝜋𝑎2
𝑏2
[𝑏2
𝑦 −
𝑦3
3
]
0
𝑏
 𝑉′
=
2𝜋𝑎2
𝑏2
[𝑏3
−
𝑏3
3
]
 𝑉′
=
4
3
𝜋𝑎2
𝑏
Reference BookandWebsite Name:
1. Advance Mathematics (Group-2) – Atul Prakashan
2. Engineering Mathematics – N.P.Bali and Dr. Manish Goyal
3. www.mathisfun.com
4. www.mathworld.com
5. www.analyze.math.com
6. https://images.search.yahoo.com

24. EXERCISE-2
Q-1. Integrate the following function w.r.t. x:
1. ∫
(1+𝑙𝑜𝑔𝑥)2
𝑥
𝑑𝑥
2. ∫
6𝑥+2
3𝑥2+2𝑥+5
𝑑𝑥
3. ∫ 𝑥 𝑛
𝑙𝑜𝑔𝑥𝑑𝑥
4. ∫ 𝑥𝑡𝑎𝑛−1
𝑥𝑑𝑥
5. ∫
𝑥+3
( 𝑥−1)(𝑥−2)
𝑑𝑥
Q-2. Evaluate the following:
1. ∫ 𝑡𝑎𝑛𝑥𝑑𝑥
𝜋
3
0
2. ∫
𝑙𝑜𝑔𝑥
𝑥
𝑑𝑥
𝑏
𝑎
3. ∫
𝑥𝑑𝑥
( 𝑥−1)(𝑥−2)
8
3
4. ∫
√5−𝑥
√5−𝑥+√𝑥
5
0
5. ∫ 𝑠𝑖𝑛5𝑥𝑐𝑜𝑠3𝑥𝑑𝑥
𝜋
2
0
Q-3. Find the Area enclosed by the parabola 𝑥2
= 4𝑦 and the line 𝑦 = 𝑥.
Q-4. Find the Area enclosed by the parabolas 𝑦2
= 4𝑎𝑥 and 𝑥2
= 4𝑎𝑦.
Q-5. Find the volume of the regular cone having radius of base r and height h.
Q-6. A line x=a intersects the parabola 𝑦2
= 4𝑎𝑥. If the area enclosed by the
parabola , the line x=a and the X-axis is revolved about the X-axis, find the volume
of the solid of revolution.