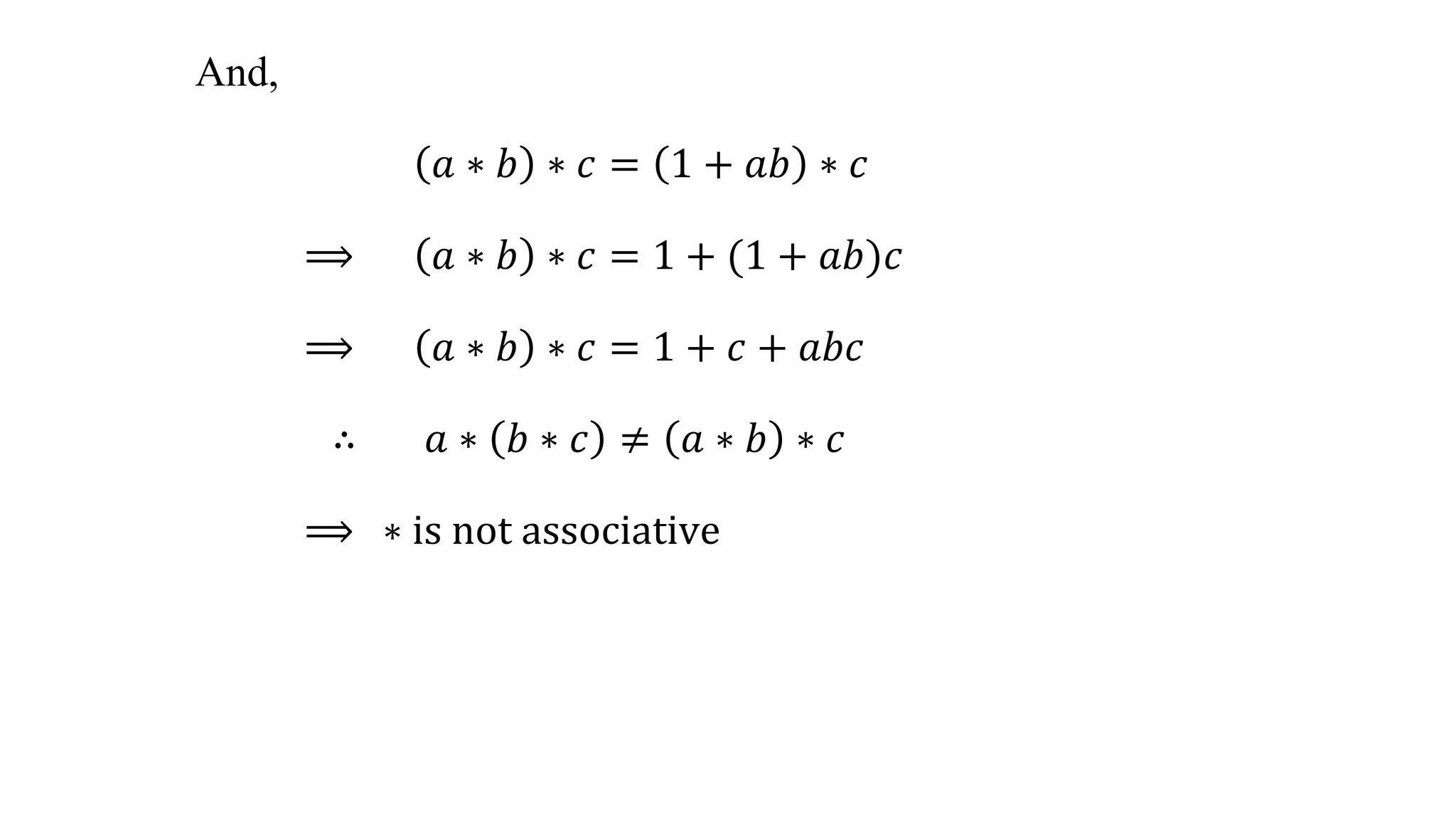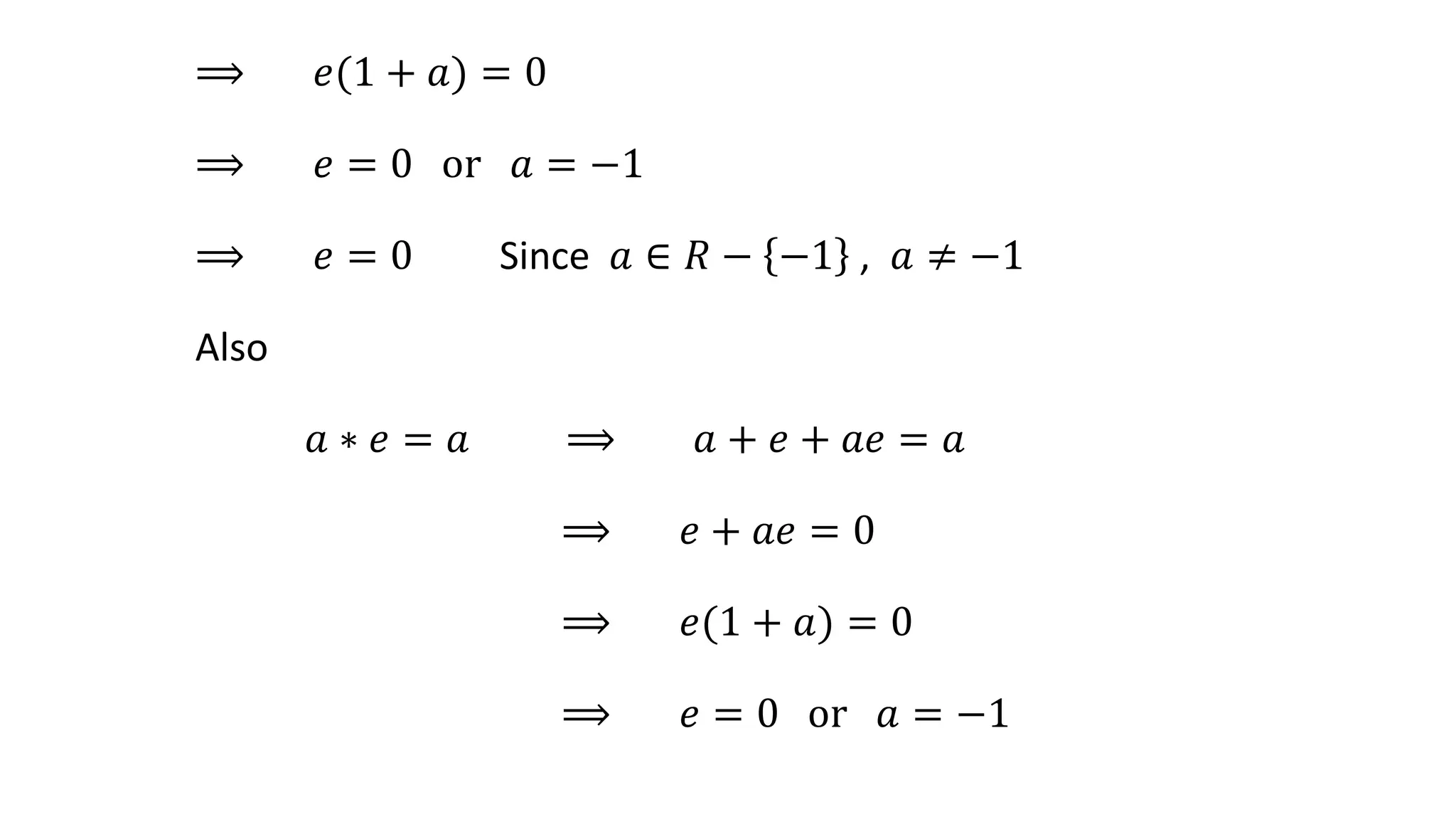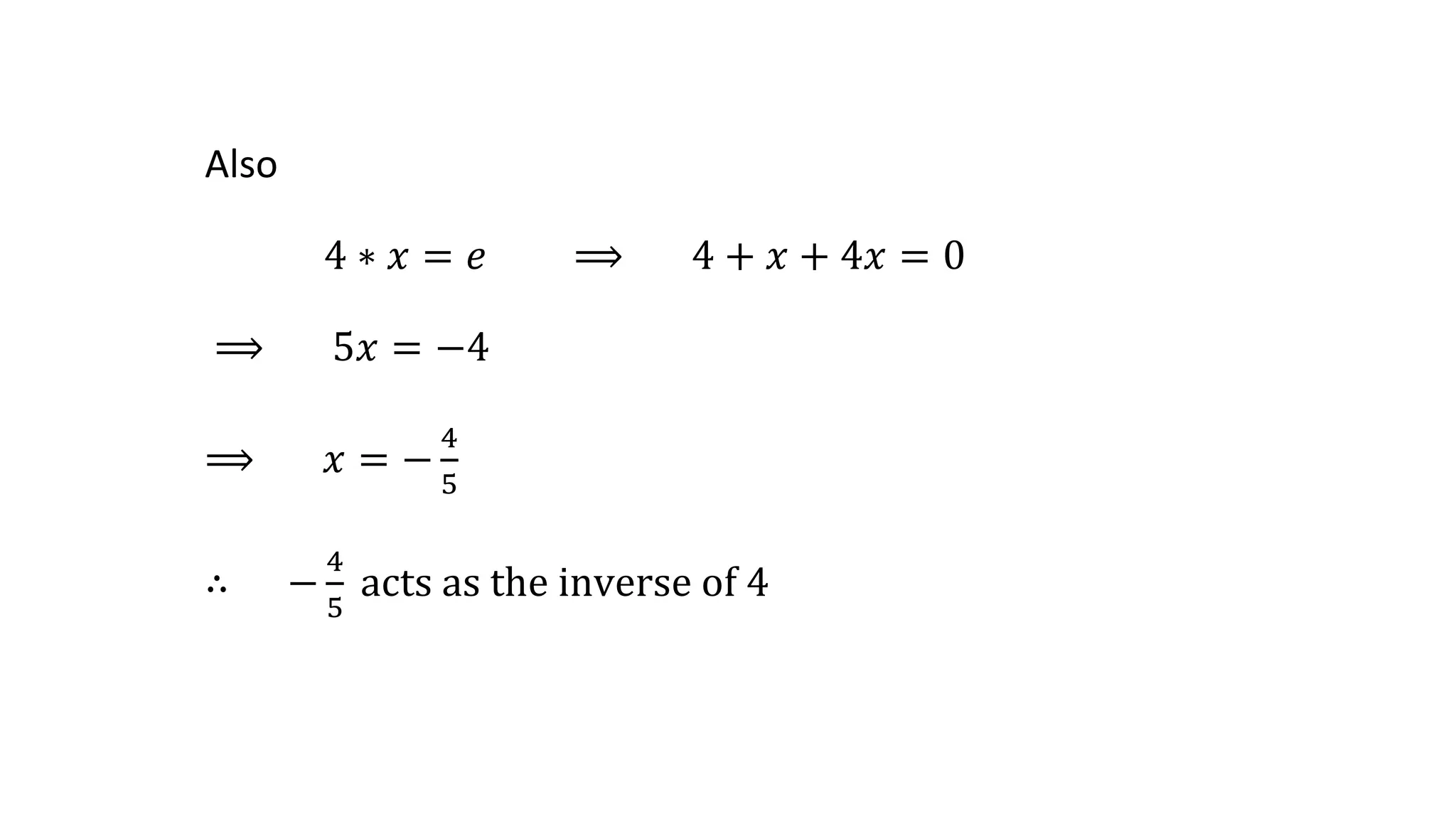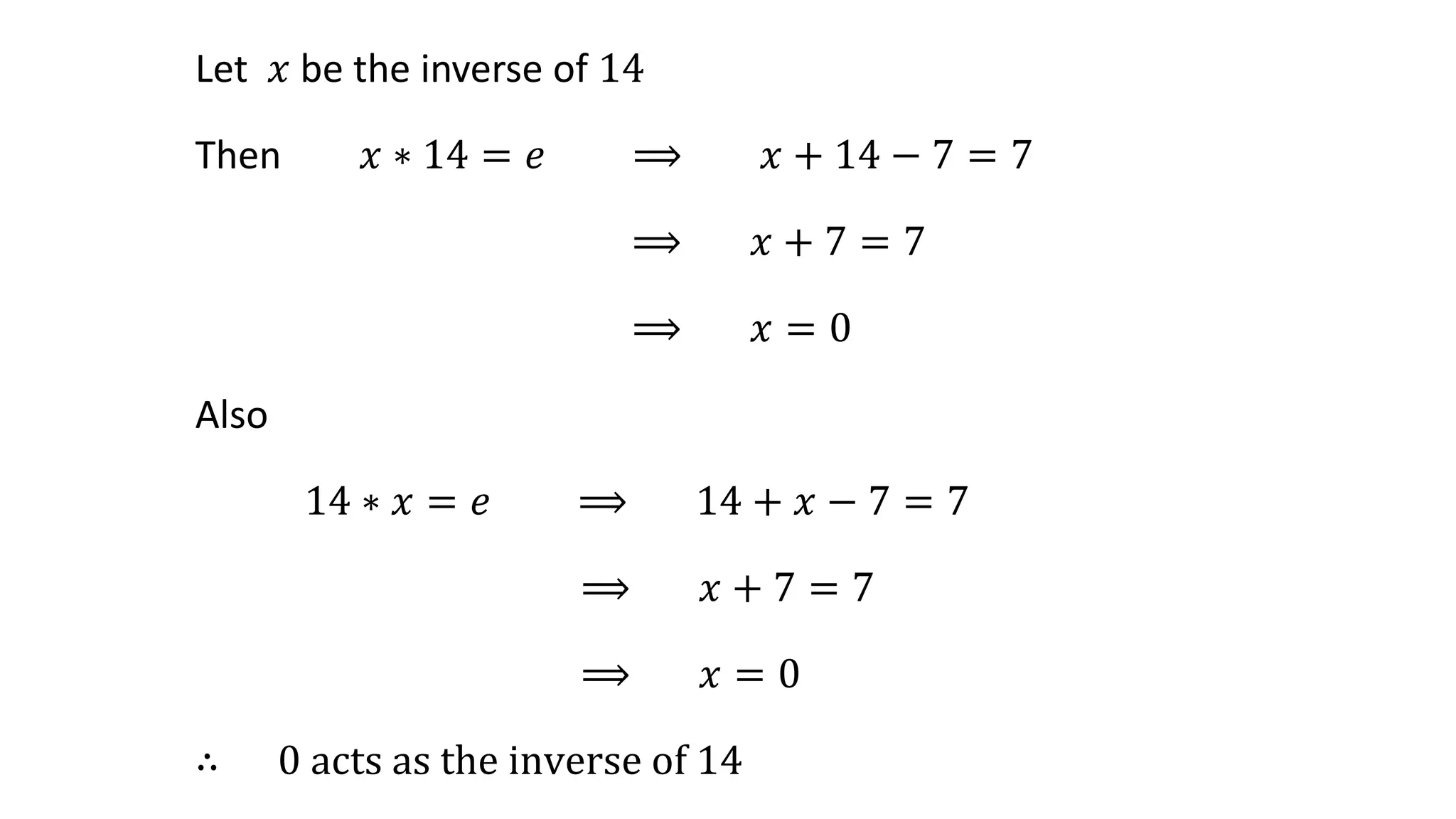The document defines various sets of numbers and binary operations. It then provides examples of binary operations on sets of numbers, such as addition and multiplication on sets of natural numbers, integers, rational numbers, real numbers, and complex numbers. The document also defines properties of binary operations such as commutativity, associativity, identity elements, and inverse elements. It provides problems and solutions showing examples of binary operations and verifying their properties.

1. BINARY OPERATIONS
Lecture:
Dr. Soya Mathew

2. Following are the notations and definitions to represent the set of
numbers:
𝑅 = Set of all real numbers
𝑅∗
= Set of all non zero real numbers
𝑄 = Set of all rational numbers
⟹ 𝑄 =
𝑝
𝑞
: 𝑝 and 𝑞 are integers and 𝑞 ≠ 0
𝑄∗
= Set of all non zero rational numbers

3. 𝑄′ = Set of all irrational numbers
⟹ 𝑄′ = 2, 𝜋, … … … … .
𝑁 = Set of all natural numbers
⟹ 𝑁 = 1, 2, 3, 4, 5 … … …
𝑍 𝑜𝑟 𝐼 = Set of all integers
⟹ 𝑍 𝑜𝑟 𝐼 = … , −3, −2, −1, 0, 1, 2, 3, …
𝐶 = Set of all complex numbers
⟹ 𝐶 = 𝑎 + 𝑖𝑏 ∶ 𝑎, 𝑏 ∈ 𝑅 and 𝑖 = −1
𝐶∗ = Set of all non zero complex numbers

4. Binary Operations (Compositions)
Let S be a non-empty set. The mapping ∗∶ 𝑆 × 𝑆 → 𝑆 which associates
each ordered pair 𝑎, 𝑏 of the elements of S to a unique element of S, denoted
by 𝑎 ∗ 𝑏 is called a binary operation or a binary composition on S.
That is,
An operation ∗ on a non-empty set S is a binary operation if and only if
∀ 𝑎 ∈ 𝑆, 𝑏 ∈ 𝑆 ⟹ 𝑎 ∗ 𝑏 ∈ 𝑆
(S is closed under binary operation ∗ )

5. Examples:
1. The usual addition (+) and multiplication (×) are binary operations on the
set of
(a) N of Natural Numbers (b) Z of integers
(c) Q of Rational Numbers (d) R of Real numbers
(e) C of Complex Numbers.
2. The usual subtraction – is not a binary operation on the set N of natural
numbers. For,
3 ∈ 𝑁, 5 ∈ 𝑁 ⟹ 3 − 5 = −2 ∉ 𝑁

6. Laws of Binary Operation
A binary operation ∗ on a non – empty set S
 is said to be commutative if
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 ∀ 𝑎, 𝑏 ∈ 𝑆
 is said to be associative if
𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 ∗ 𝑏 ∗ 𝑐 ∀ 𝑎, 𝑏, 𝑐 ∈ 𝑆
 is said to have an identity element if ∃ 𝑒 ∈ 𝑆 such that
𝑒 ∗ 𝑎 = 𝑎 ∗ 𝑒 = 𝑎 ∀ 𝑎 ∈ 𝑆
 is said to have an inverse element if ∃ 𝑏 ∈ 𝑆 such that
𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎 = 𝑒 ∀ 𝑎 ∈ 𝑆 , 𝑒 ∈ 𝑆

7. Problems
1. A binary operation ∗ is defined on the set Z of integers by 𝒂 ∗ 𝒃 = 𝟏 + 𝒂𝒃
∀ 𝒂, 𝒃 ∈ 𝒁. Show that ∗ is commutative but not associative.
Solution:
By definition, 𝑎 ∗ 𝑏 = 1 + 𝑎𝑏 ∀ 𝑎, 𝑏 ∈ 𝑍
Now,
𝑏 ∗ 𝑎 = 1 + 𝑏𝑎
⟹ 𝑏 ∗ 𝑎 = 1 + 𝑎𝑏 (Since usual multiplication is commutative)

8. ∴ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
⟹ ∗ is commutative
Next
Let 𝑎, 𝑏, 𝑐 be any three elements of Z
Consider,
𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 ∗ (1 + 𝑏𝑐)
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 1 + 𝑎(1 + 𝑏𝑐)
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 1 + 𝑎 + 𝑎𝑏𝑐

9. And,
𝑎 ∗ 𝑏 ∗ 𝑐 = 1 + 𝑎𝑏 ∗ 𝑐
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 1 + (1 + 𝑎𝑏)𝑐
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 1 + 𝑐 + 𝑎𝑏𝑐
∴ 𝑎 ∗ 𝑏 ∗ 𝑐 ≠ 𝑎 ∗ 𝑏 ∗ 𝑐
⟹ ∗ is not associative

10. 2. In the set 𝑹∗of non-zero real numbers the binary operations ∗ is defined by
𝒂 ∗ 𝒃 =
𝒂𝒃
𝟑
∀ 𝒂, 𝒃 ∈ 𝑹∗. Show that the inverse of 9 is 1.
Solution:
By definition 𝑎 ∗ 𝑏 =
𝑎𝑏
3
∀ 𝑎, 𝑏 ∈ 𝑅∗
Let 𝑒 ∈ 𝑅∗ be the identity element
Then
𝑒 ∗ 𝑎 = 𝑎 ⟹
𝑒𝑎
3
= 𝑎
⟹ 𝑒 = 3

11. Also
𝑎 ∗ 𝑒 = 𝑎 ⟹
𝑎𝑒
3
= 𝑎
⟹ 𝑒 = 3
∴ 3 acts as the identity element
Let 𝑥 be the inverse of 9
Then
𝑥 ∗ 9 = 𝑒 ⟹
𝑥9
3
= 3
⟹ 𝑥 = 1

12. Also
9 ∗ 𝑥 = 𝑒 ⟹
9𝑥
3
= 3
⟹ 𝑥 = 1
∴ 1 acts as the inverse of 9

13. 3. If in the set of real numbers other than −𝟏, the operation ∗ is defined by
𝒂 ∗ 𝒃 = 𝒂 + 𝒃 + 𝒂𝒃 ∀ 𝒂, 𝒃 ∈ 𝑹 − −𝟏 . Show that the identity element is
𝟎 and the inverse of 𝟒 is −
𝟒
𝟓
.
Solution:
By definition 𝑎 ∗ 𝑏 = 𝑎 + 𝑏 + 𝑎𝑏 ∀ 𝑎, 𝑏 ∈ 𝑅 − −1
Let 𝑒 ∈ 𝑅 − −1 be the identity element
Then
𝑒 ∗ 𝑎 = 𝑎 ⟹ 𝑒 + 𝑎 + 𝑒𝑎 = 𝑎
⟹ 𝑒 + 𝑒𝑎 = 0

14. ⟹ 𝑒(1 + 𝑎) = 0
⟹ 𝑒 = 0 or 𝑎 = −1
⟹ 𝑒 = 0 Since 𝑎 ∈ 𝑅 − −1 , 𝑎 ≠ −1
Also
𝑎 ∗ 𝑒 = 𝑎 ⟹ 𝑎 + 𝑒 + 𝑎𝑒 = 𝑎
⟹ 𝑒 + 𝑎𝑒 = 0
⟹ 𝑒(1 + 𝑎) = 0
⟹ 𝑒 = 0 or 𝑎 = −1

15. ⟹ 𝑒 = 0 Since 𝑎 ∈ 𝑅 − −1 , 𝑎 ≠ −1
∴ 0 acts as the identity element
Let 𝑥 be the inverse of 4
Then
𝑥 ∗ 4 = 𝑒 ⟹ 𝑥 + 4 + 𝑥4 = 0
⟹ 5𝑥 = −4
⟹ 𝑥 = −
4
5

16. Also
4 ∗ 𝑥 = 𝑒 ⟹ 4 + 𝑥 + 4𝑥 = 0
⟹ 5𝑥 = −4
⟹ 𝑥 = −
4
5
∴ −
4
5
acts as the inverse of 4

17. 4. If the binary operation ∗ on the set 𝑹 of real numbers is defined by
𝒂 ∗ 𝒃 = 𝒂 + 𝒃 − 𝟕 ∀ 𝒂, 𝒃 ∈ 𝑹. Show that ∗ is commutative and
associative. Also find the identity element and the inverse of 𝟏𝟒.
Solution:
By definition 𝑎 ∗ 𝑏 = 𝑎 + 𝑏 − 7 ∀ 𝑎, 𝑏 ∈ 𝑅
Now, 𝑏 ∗ 𝑎 = 𝑏 + 𝑎 − 7
⟹ 𝑏 ∗ 𝑎 = 𝑎 + 𝑏 − 7 (Since usual addition is commutative)
∴ 𝑎 ∗ 𝑏 = 𝑏 ∗ 𝑎
⟹ ∗ is commutative

18. Let 𝑎, 𝑏, 𝑐 be any three elements of 𝑅
Now, 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 ∗ 𝑏 + 𝑐 − 7
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 + 𝑏 + 𝑐 − 7 − 7
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 + 𝑏 + 𝑐 − 14
Next, 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 + 𝑏 − 7 ∗ 𝑐
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 + 𝑏 − 7 + 𝑐 − 7
⟹ 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 + 𝑏 + 𝑐 − 14
∴ 𝑎 ∗ 𝑏 ∗ 𝑐 = 𝑎 ∗ 𝑏 ∗ 𝑐
⟹ ∗ is associative

19. Let 𝑒 ∈ 𝑅 be the identity element
Then
𝑒 ∗ 𝑎 = 𝑎 ⟹ 𝑒 + 𝑎 − 7 = 𝑎
⟹ 𝑒 − 7 = 0
⟹ 𝑒 = 7
Also 𝑎 ∗ 𝑒 = 𝑎 ⟹ 𝑎 + 𝑒 − 7 = 𝑎
⟹ 𝑒 − 7 = 0
⟹ 𝑒 = 7
∴ 7 acts as the identity element

20. Let 𝑥 be the inverse of 14
Then 𝑥 ∗ 14 = 𝑒 ⟹ 𝑥 + 14 − 7 = 7
⟹ 𝑥 + 7 = 7
⟹ 𝑥 = 0
Also
14 ∗ 𝑥 = 𝑒 ⟹ 14 + 𝑥 − 7 = 7
⟹ 𝑥 + 7 = 7
⟹ 𝑥 = 0
∴ 0 acts as the inverse of 14