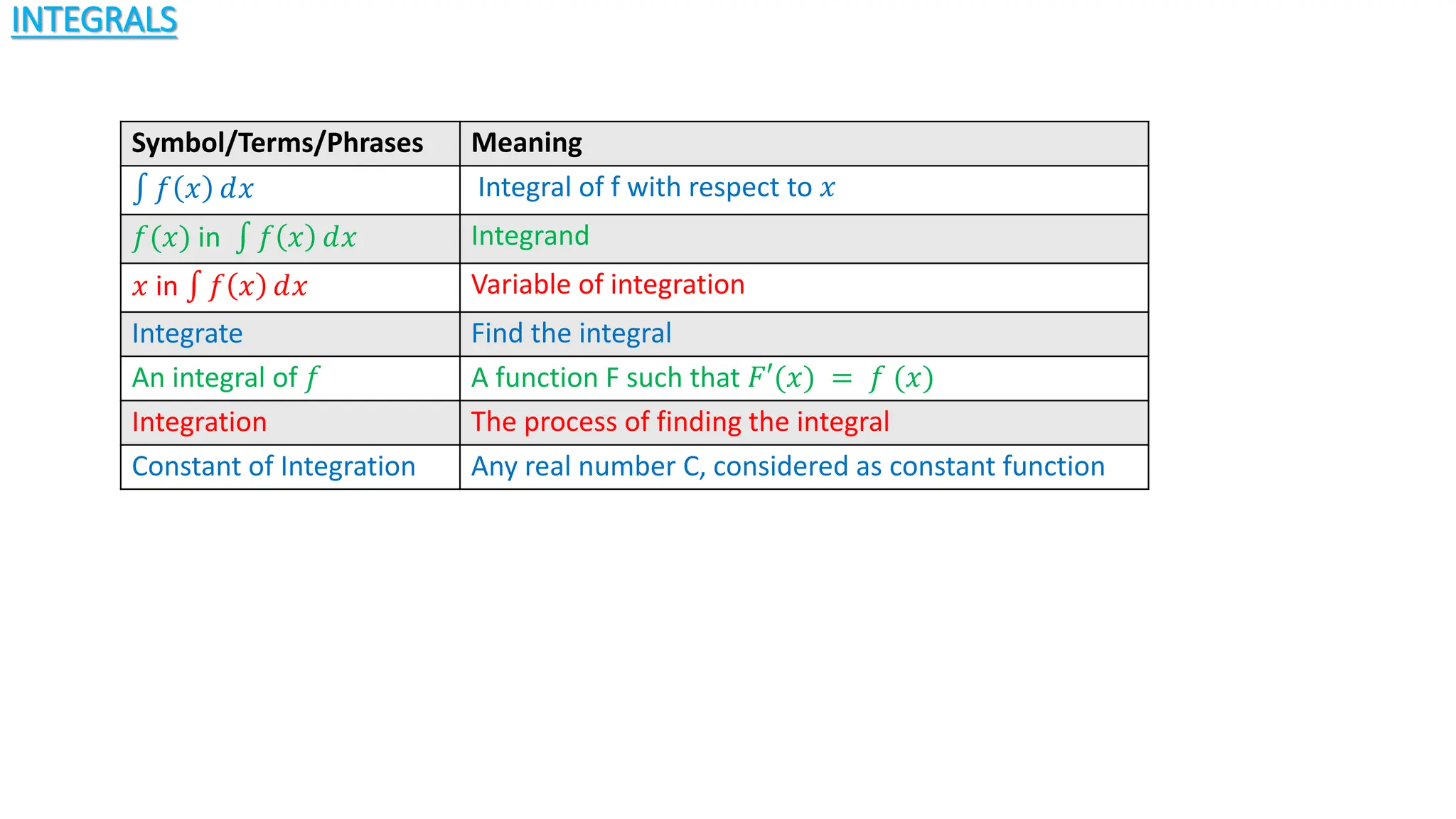
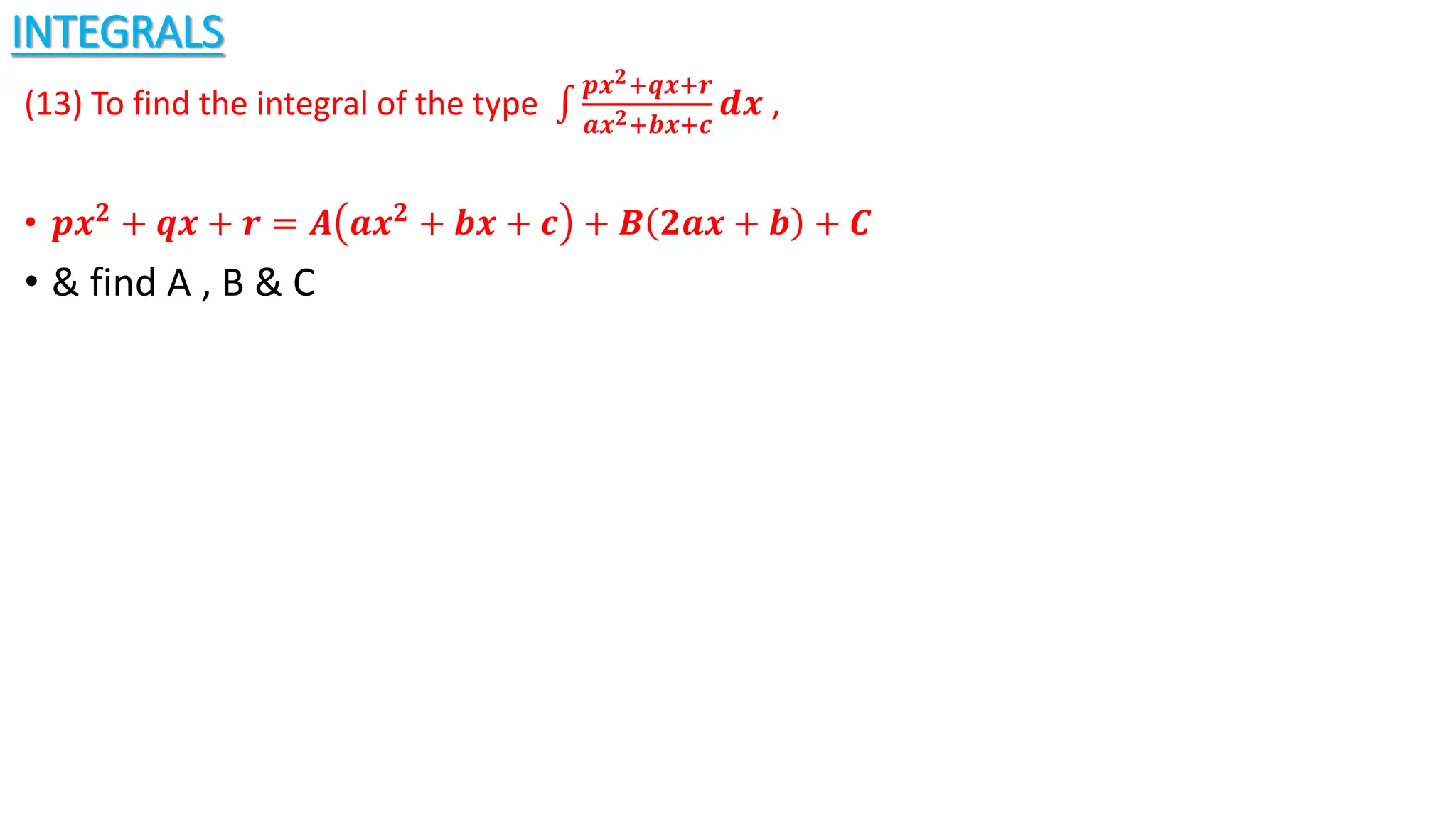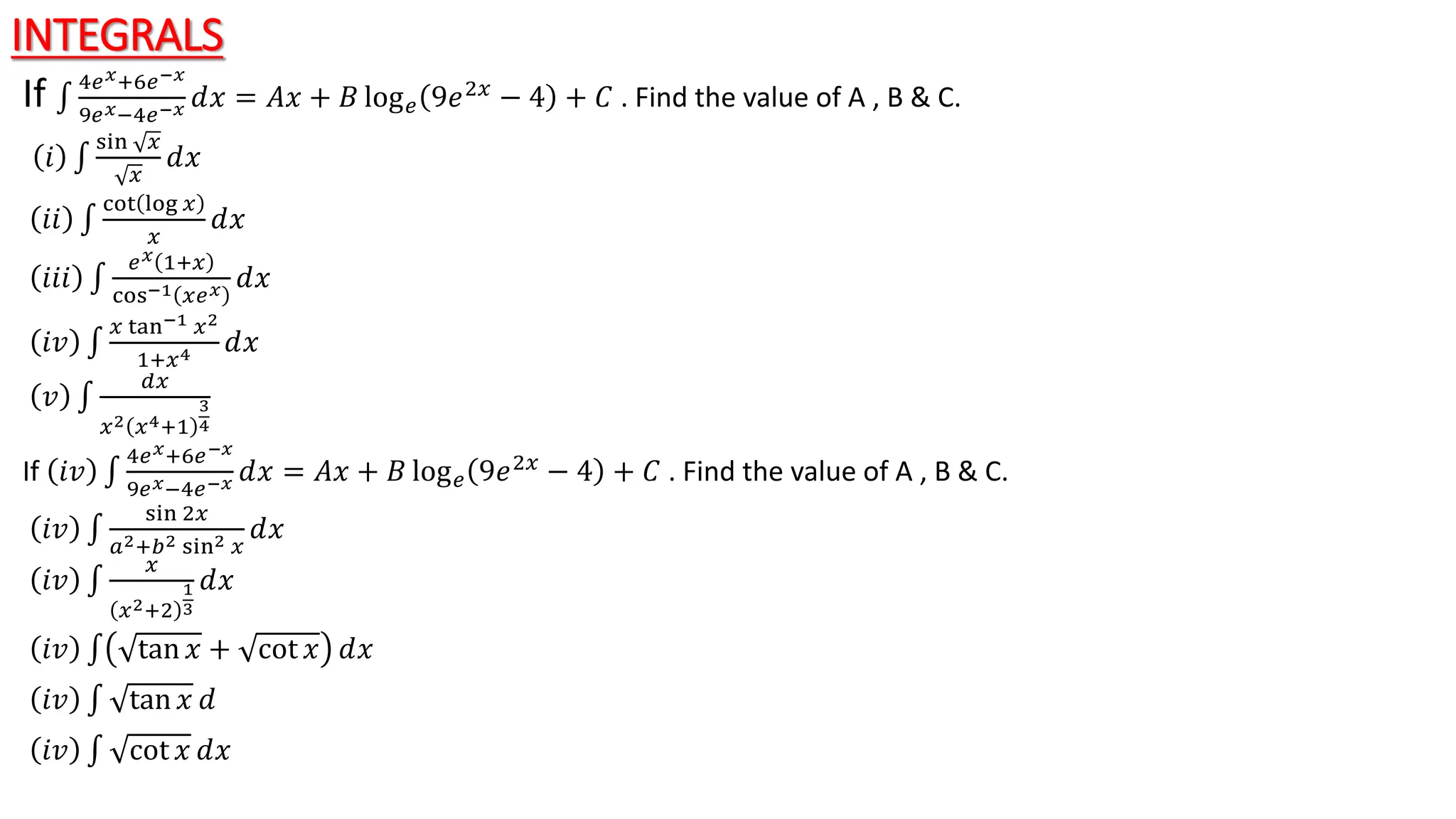1) This document defines key terms and formulas related to integrals and integration. It discusses integrals of algebraic, trigonometric, exponential, and other functions.
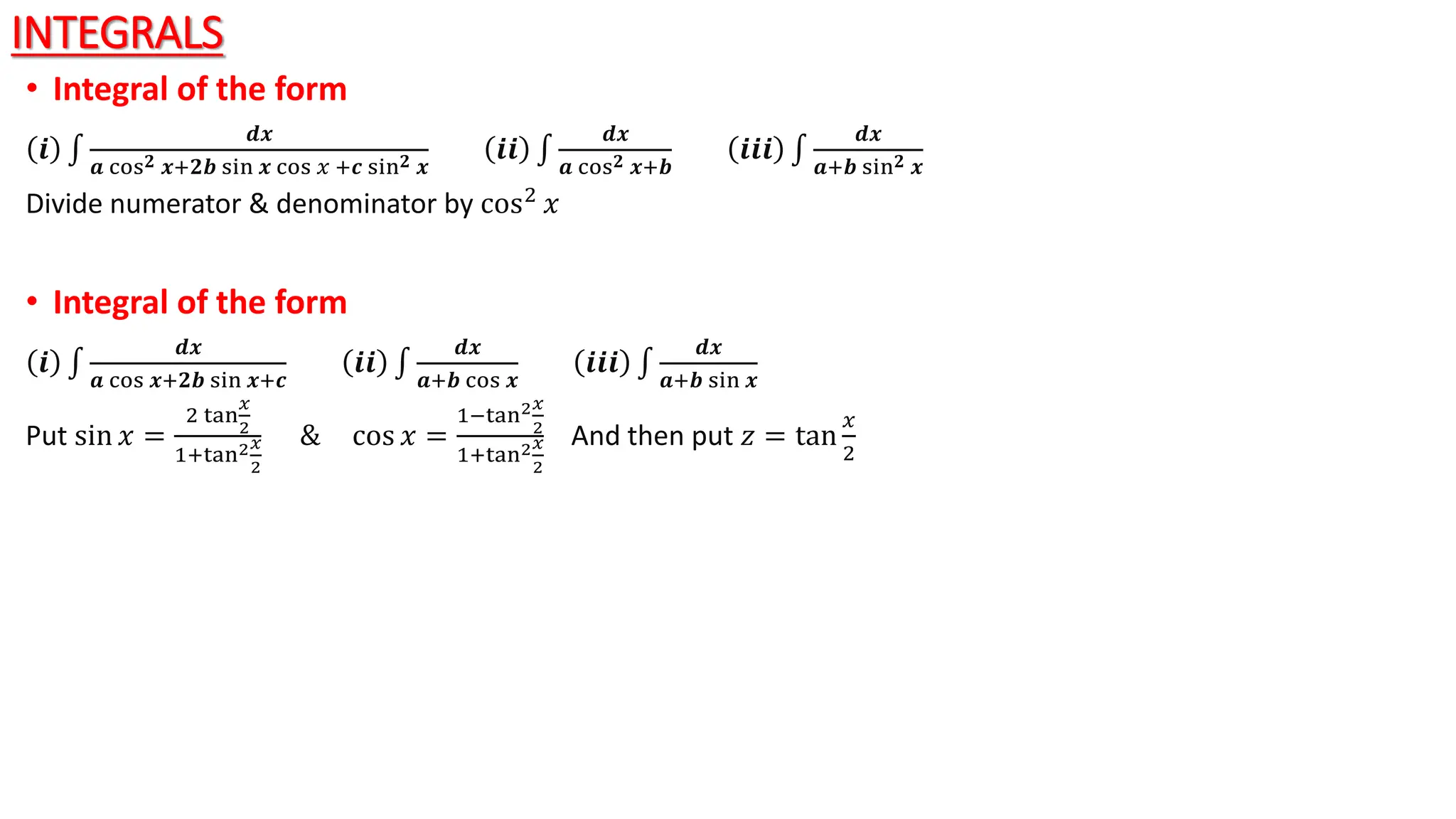
2) Formulas are provided for finding integrals of trigonometric functions involving sin, cos, tan, cot, sec, and csc. The document also discusses integration techniques like substitution and using trigonometric identities.
3) Examples are given to demonstrate finding integrals of various functions like algebraic functions, exponential functions, trigonometric functions, and functions that can be reduced to trigonometric form using substitution. Integration methods like substitution, using properties of derivatives, and trigonometric identities are also explained.