Downloaded 96 times
Uploaded byHarshana Madusanka Jayamaha
Linear and non linear equation
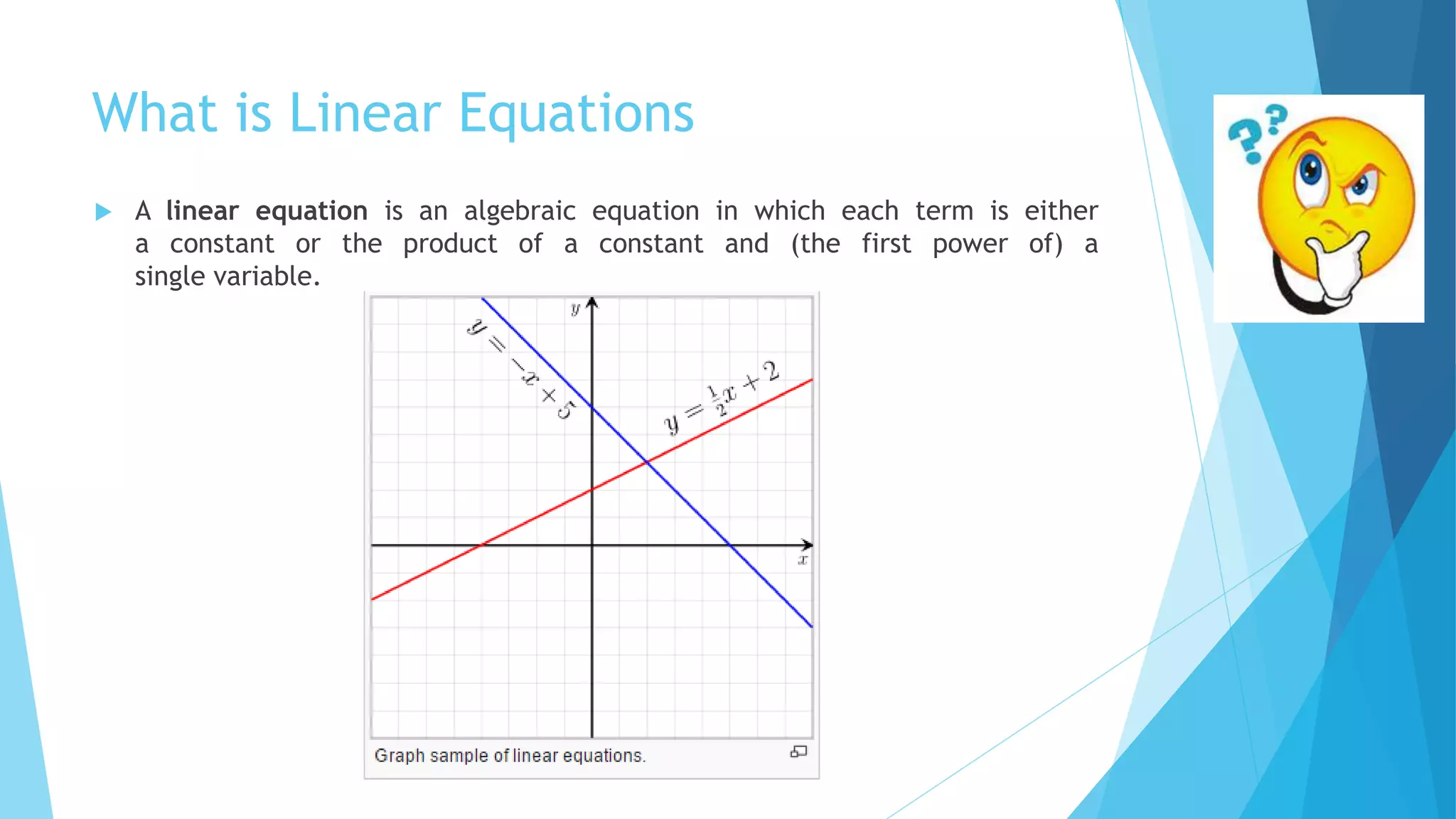
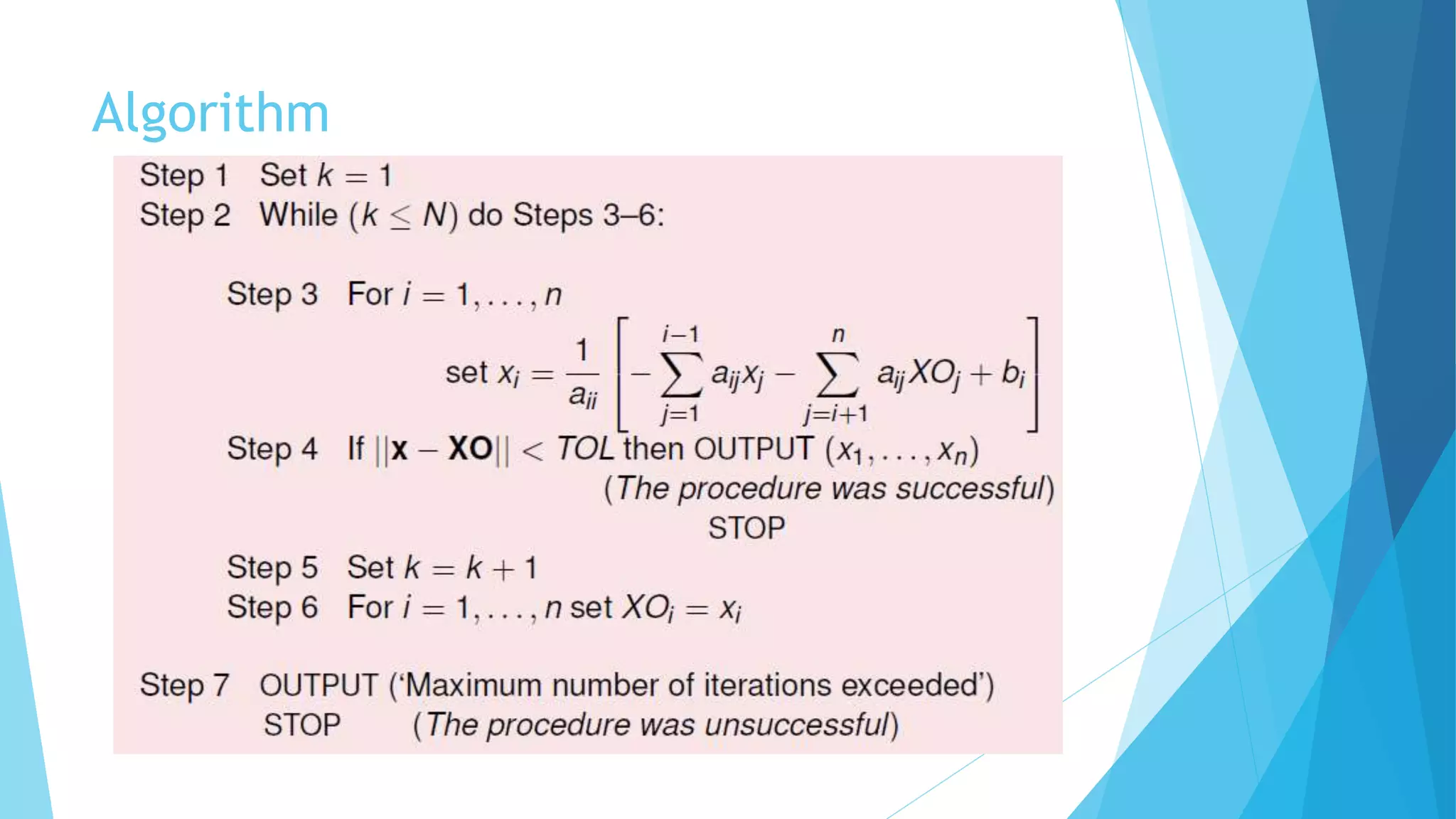
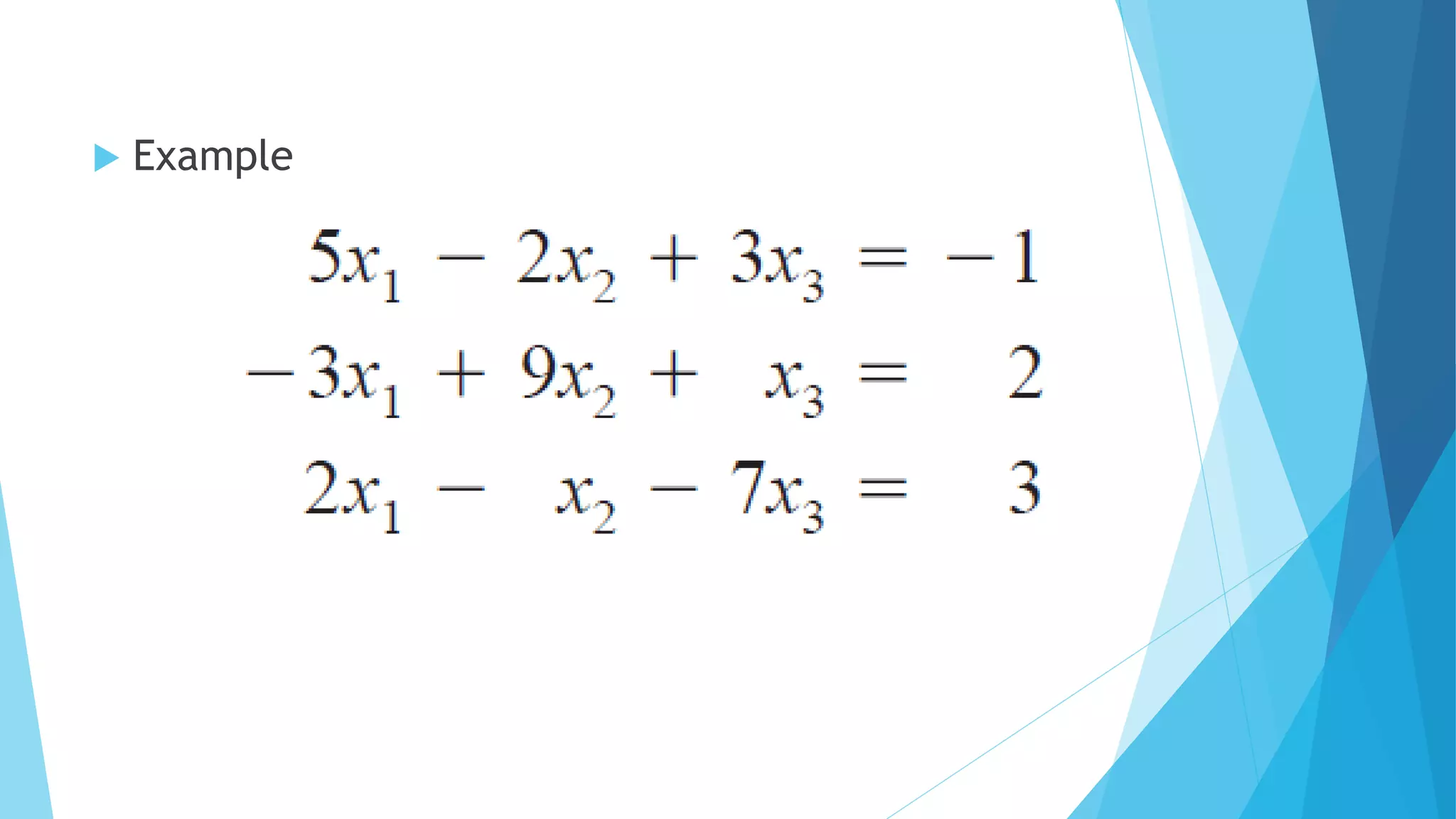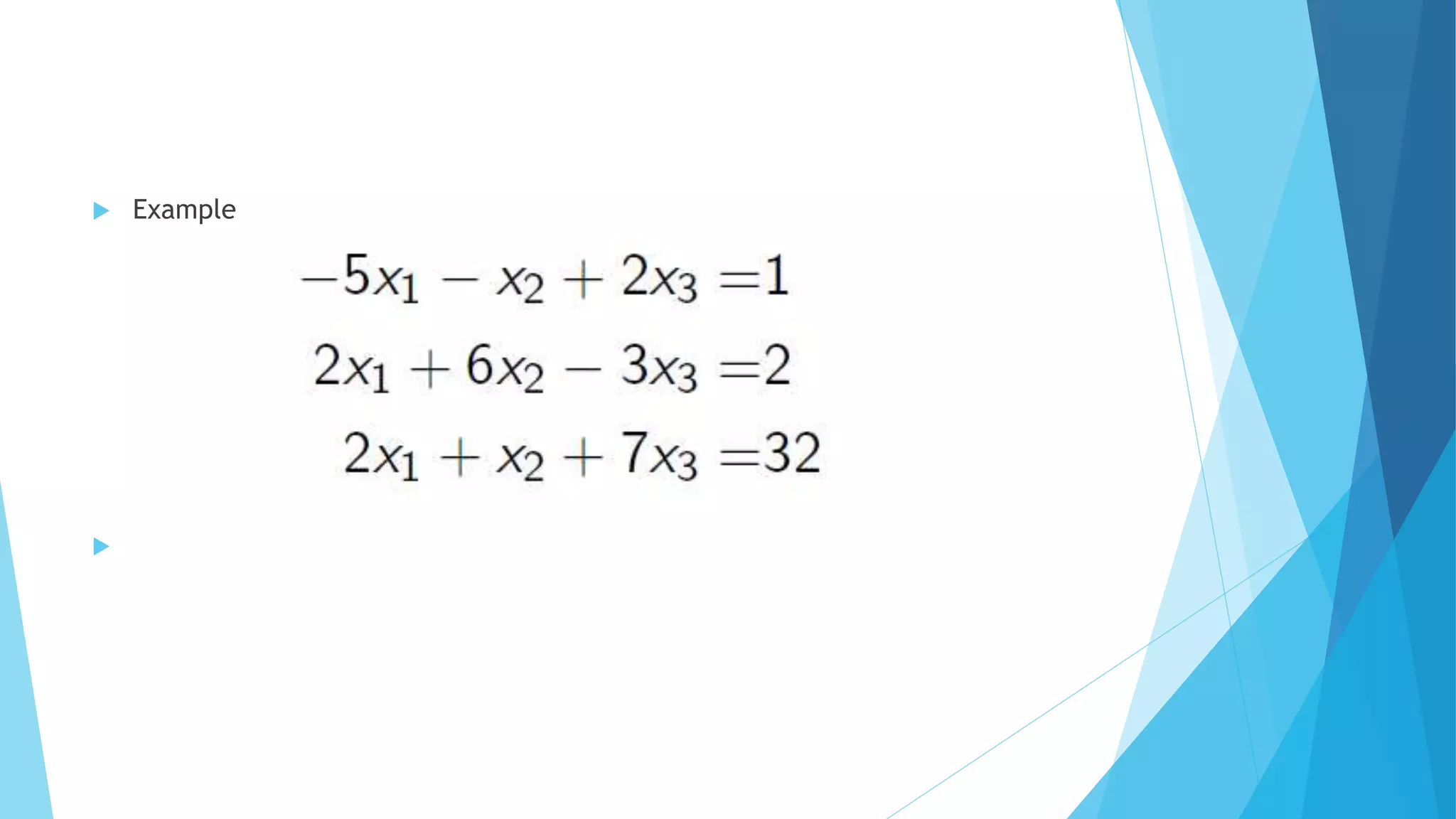This document discusses methods for solving systems of linear equations. It describes direct methods like Gauss elimination and LU decomposition that obtain solutions in a finite number of steps. It also describes iterative methods like Jacobi's method and Gauss-Seidel method that obtain solutions through successive approximations that converge to the required solution. Pseudocode and MATLAB implementations are provided for various algorithms.
More Related Content
Similar to Linear and non linear equation
Linear and non linear equation
- 1. computing discrete approximation ofsolution of linear simultaneous equation JMHM Jayamaha
- 2. Content Linear Equations What is Linear Equations Method for solving the system of linear equations Direct Method Gauss Elimination method LU Decomposition Iterative method Jacobi's method Gauss Seidal method
- 3.
- 4. What is LinearEquations A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable.
- 5. Two methods forsolving the system of linear equations Direct Method Solutions are obtained through a finite number of arithmetic operations Gauss Elimination method LU Decomposition Iterative Method: Solutions are obtained through a sequence of successive approximations which converges to the required solution Jacobi's method Gauss Seidal method
- 6. GAUSS – ELIMINATIONMETHOD
- 7. GAUSS – ELIMINATIONMETHOD Consider a system of 3 – equations with 3 – unknowns )1( 3333232131 2323222121 1313212111 bxaxaxa bxaxaxa bxaxaxa
- 8. Form the augmentedmatrix from the given equations as 3333231 2232221 1131211 baaa baaa baaa 1 11 21 22operationrowtheUse R a a RR 1 11 31 33operationrowtheUse R a a RR If a11 0
- 9. New augmented matrixwill be '''0 '''0 33332 22322 1131211 baa baa baaa
- 10. 2 22 32 33 ' ' operationrowtheUse R a a RR Newaugmented matrix will be ''''00 '''0 333 22322 1131211 ba baa baaa If a22’ 0
- 11. From the lastmatrix, the equations can be written as '''' ''' 3333 2323222 1313212111 bxa bxaxa bxaxaxa
- 12. Use back substitutionto get the solution as 11 3132121 1 22 3232 2 33 3 3 , ' '' , '' '' a xaxab x a xab x a b x
- 13. Gauss Elimination methodMatlab Implementation function x = Gauss(A,b); n = length(b); x = zeros(n,1); for k=1:n-1 % forward elimination for i=k+1:n xmult = A(i,k)/A(k,k); for j=k+1:n A(i,j) = A(i,j)-xmult*A(k,j); end b(i) = b(i)-xmult*b(k); end end % back substitution x(n) = b(n)/A(n,n); for i=n-1:-1:1 sum = b(i); for j=i+1:n sum = sum-A(i,j)*x(j); end x(i) = sum/A(i,i); end
- 14.
- 15. Matrix Ais decomposed into a product of a lower triangular matrix L and an upper triangular matrix U, that is A = LU or 100 10 1 0 00 23 1312 333231 2221 11 333231 232221 131211 u uu lll ll l aaa aaa aaa
- 16. Matrices L andU can be obtained by the following rule 1. Step 1: Obtain l11 = a11, l21 = a21, l31 = a31 11 13 13 11 12 12 ,Obtain:2Step.2 a a u a a u 3. Step 3: Obtain l22 = a22 – l21u12 132123 22 23 1 Obtain:4Step.4 ula l u 5. Step 5: Obtain l32 = a32 – l31u12 6. Step 6: Obtain l33 = a33 – l31u13 – l32u23
- 17. Once lower andupper triangular matrices are obtained the solution of Ax = b can be obtained using the procedure Ax = b LUx = b Let Ux = y then LUx = b Ly = b
- 18. Steps to getthe solution of linear equations 3 2 1 3 2 1 333231 2221 11 0 00 b b b y y y lll ll l bLy 2321313 33 3 1212 22 2 11 1 1 1 and 1 ,where ylylb l y ylb l y l b y By Forward substitution
- 19.
- 20. Matlab Implementation forLU Decomposition
- 21.
- 22. The Jacobi Method This method makes two assumptions 1. that the system given by has a unique solution 2. the coefficient matrix A has no zeros on its main diagonal
- 23. To beginthe Jacobi method, solve the first equation for x1 the second equation for x2 and so on, as follows. Then make an initial approximation of the solution,
- 24.
- 25.
- 26. To begin,write the system in the form Because you do not know the actual solution, choose
- 27. as aconvenient initial approximation. So, the first approximation is Continuing this procedure, you obtain the sequence of approximations shown in Table
- 28. Because thelast two columns in Table are identical, you can conclude that to three significant digits the solution is
- 29. Matlab Implementation forjacobi method
- 30.
- 31. Gauss-Seidel iterationis similar to Jacobi iteration, except that new values for xi are used on the right-hand side of the equations as soon as they become available. It improves upon the Jacobi method in two respects Convergence is quicker, since you benefit from the newer, more accurate xi values earlier. Memory requirements are reduced by 50%, since you only need to keep track of one set of xi values, not two sets.
- 32.
- 33.
- 34. Step 1:reformat the equations, solving the first one for x1, the second for x2, and the third for x3
- 35. Step 2a:Substitute the initial guesses for xi into the right-hand side of the first equation Step 2b: Substitute the new x1 value with the initial guess for x3 into the second equation Step 2c: Substitute the new x1 and x2 values into the third equation
- 36. Step 3,4, · · · : Repeat step 2 and watch for the xi values to converge to an exact solution.
- 37. Matlab Implementation ofGauss-Seidel Method
- 38. Summary Solution oflinear simultaneous are discussed. Two methods Direct Gauss Elimination method LU Decomposition Iterative Jacobi's method Gauss Seidal method
- 39. References https://en.wikipedia.org/wiki/Linear_equation(2016-06-15) http://homel.vsb.cz/~dom033/predmety/parisLA/02_direct_methods.pdf Numerical computational methods by P.B Patill , U.P Verma http://college.cengage.com/mathematics/larson/elementary_linear/5e/stud ents/ch08-10/chap_10_2.pdf http://ocw.usu.edu/Civil_and_Environmental_Engineering/Numerical_Method s_in_Civil_Engineering/NonLinearEquationsMatlab.pdf http://people.whitman.edu/~hundledr/courses/M467/GaussSeidel.pdf
Editor's Notes
- #5 A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable
- #8 It is a direct method for finding the solution of a system of linear equations and is based on the principle of elimination. where aij(1)’s (i, j = 1, 2, 3) are the coefficient of unknowns and bi(1)’s (i = 1, 2, 3) are prescribed constants
- #23 If any of the diagonal entries a11, a22, . . . , ann are zero, then rows or columns must be interchanged to obtain a coefficient matrix that has nonzero entries on the main diagonal.
- #24 To begin the Jacobi method, solve the first equation for x1 the second equation for x2 and so on, as follows. Initial Approximation and substitute these values of xi into the right-hand side of the rewritten equations to obtain the first approximation. After this procedure has been completed, one iteration has been performed.
- #26 In the same way, the second approximation is formed by substituting the first approximation’s x-values into the right-hand side of the rewritten equations. By repeated iterations, you will form a sequence of approximations that often converges to the actual solution.
- #31 Iterative methods provide an alternative approach that an iterative methods starts with an approximate solution , and uses it by means of a recrurrence fomula to provie another approximate solution ; by repeatedly applying the formula, a sequence of solution is abtained with ( under suitable conditions)( converges to the exact solution . Iterative methods have the advantages of simplicity of operation and ease of implementation of computers. And they are realativelyi insensitive to propagation of errors; they would be used in preference to direct methods for solving lenear systems involving several handred variables. Particularly , if many of the coefficients were zero . Systems of over 100000 variable have more variables are difficult or impossible to solve by direct methods.