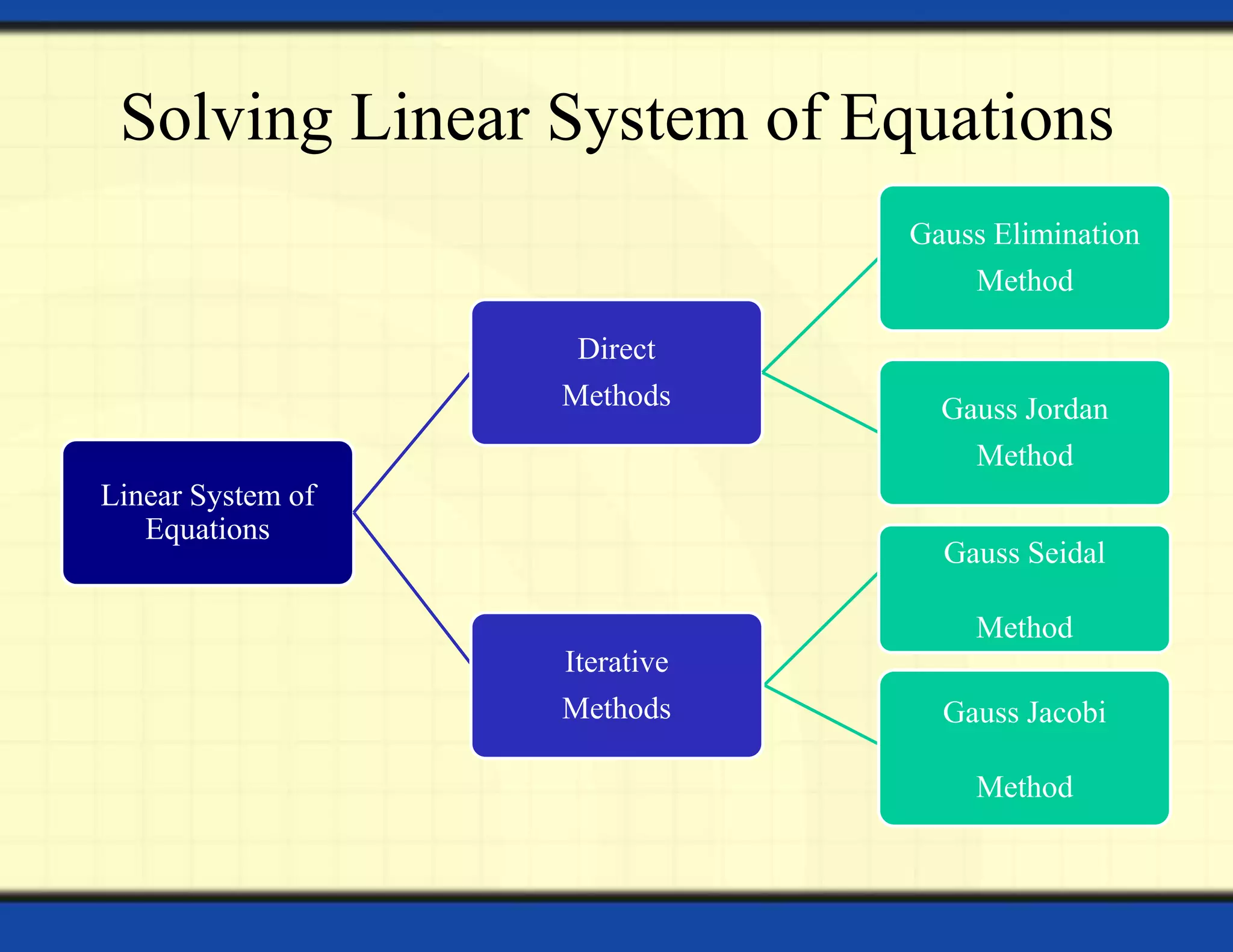
The document discusses methods for solving systems of linear equations. It introduces Gauss elimination and Gauss Jordan methods. Gauss elimination transforms the augmented matrix of the system into row echelon form through elementary row operations, then back-substitutes to solve for the variables. Gauss Jordan additionally transforms the matrix to reduced row echelon form to read solutions directly from the matrix. An example demonstrates applying each method to solve a system of equations.

1. Subject :- Numerical and Statistical Methods
Topic :- Gauss Elimination & Gauss Jordan Method

2. Contents
• System of Equations
• System of Linear Equation
• Solving Linear System of Equations
• Gauss Elimination Method
• Gauss Jordan Method
• Applications of Gaussian Method
• References

3. System of Equations
• A set of equations is called a system of
equations.
• The solutions must satisfy each equation
in the system.
• If all equations in a system are linear, the
system is a system of linear equations, or
a linear system.

4. System of Linear Equations
• Representation of system of linear equation :
a11x1 + a12x2 + ··· + a1nxn = b1
a21x1 + a22x2 + ··· + a2nxn = b2
. .
. .
am1x1 + am2x2 + ··· + amnxn = bm

5. System of Linear Equations
• In matrix form : A X = B
11 12 13 1n 1 1
21 22 23 2n 2 2
3 331 32 33 3n
n nn1 n2 n3 nn
a a a a x b
a a a a x b
=x ba a a a
x ba a a a
     
        
     
     
         
K
K
K
M MM
K

6. Solving Linear System of Equations
Linear System of
Equations
Direct
Methods
Gauss Elimination
Method
Gauss Jordan
Method
Iterative
Methods
Gauss Seidal
Method
Gauss Jacobi
Method

7. Carl Friedrich Gauss
1777-1855

8. Gauss Elimination Method
1. Write the system of equation in matrix form.
Form the augmented matrix [a | b]
2. Use row operations to transform the augmented
matrix into the form Row Echelon Form
(REF)
Row Echelon
Matrix
11 12 1n 1 1 11 12 1n 1
21 22 2n 2 2 21 22 2n 2
n1 n2 nn n n n1 n2 nn n
a a a x b a a a b
a a a x b a a a b
a a a x b a a a b
      
              
             
L L
L L
M M O M M M M M O M M
L L

9. 3. An elementary row operation is one of the
following:
• Interchange two rows.
• Multiply a row by a nonzero constant.
• Add a multiple of a row to another row.
4. Inspect the resulting matrix and re-interpret it as
a system of equations
• No Solution
• Infinite no. of solutions
• Exactly one solution

10. Example :
Q : Solve the following set of equations using
Gauss Elimination Method
x + y + z = 6
2x – y + z = 3
x + z = 4
Solution:

12. • Now re-interpret the augmented matrix as a
system of equations, starting at the bottom
and working backwards (back
substitution).
1. 0x + 0y + z = 3 so z = 3
2. 0x + y + 0z = 2 so y = 2
3. x+ y +z = 6. . Substitute the values z = 3 and
y = 2 into the equation and get x = 1

13. Gauss Jordan Method
1. Write the augmented matrix of the system
2. Use row operations to transform the augmented
matrix into the form Reduced Row Echelon
Form (RREF)
Reduced
Row Echelon
Matrix
11 12 1n 1 1 11 12 1n 1
21 22 2n 2 2 21 22 2n 2
n1 n2 nn n n n1 n2 nn n
a a a x b a a a b
a a a x b a a a b
a a a x b a a a b
      
              
             
L L
L L
M M O M M M M M O M M
L L

14. 3. An elementary row operation is one of the
following:
• Interchange two rows.
• Multiply a row by a nonzero constant.
• Add a multiple of a row to another row.
4. Inspect the resulting matrix and re-interpret it as
a system of equations
• No Solution
• Infinite no. of solutions
• Exactly one solution

15. Example :
Q : Solve the following set of equations using
Gauss Jordan Method
x + y + z = 5
2x + 3y + 5z = 8
4x + 5z = 2
Solution:

18. REFERENCES
• www.epcc.edu/Gauss-Jordan_Method
• www.Pages.pacificcoast.net/cazelais/Gauss
-Jordan_elimination_Method.pdf
• www.personal.soton.ac.uk/workbook_8_3
_gauss_elim.pdf