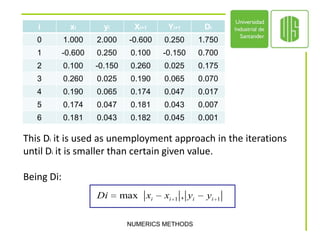
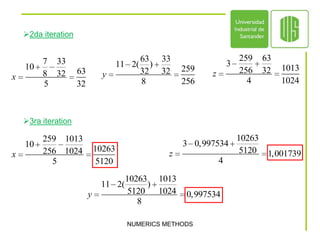
This document discusses iterative methods for solving systems of equations, including Jacobi, Gauss-Seidel, and Gauss-Seidel relaxation methods. Iterative methods progressively calculate approximations to the solution, unlike direct methods which require completing the full process to obtain the answer. The Jacobi method can solve simple square systems of equations in an iterative fashion. Gauss-Seidel is also an iterative technique that sequentially solves for each unknown using previous approximations. Gauss-Seidel relaxation is similar but incorporates a relaxation parameter. Examples demonstrate applying these methods to solve systems of equations.

1. SOLUTION OF EQUATIONS FOR ITERATIVOS METHODSBY:DUBAN CASTRO FLOREZ NUMERICS METHODS IN ENGINEERING2010

2. JACOBIA iterative method is a method that progressively it calculates approaches to the solution of a problem. To difference of the direct methods, in which the process should be finished to have the answer, in the iterative methods you can suspend the process to the i finish of an iteration and an approach is obtained to the solution.For example the method of Newton-RaphsonNUMERICS METHODS

3. NUMERICS METHODS

4. NUMERICS METHODSThe Jacobi method de is the iterative method to solve system of equations simple ma and it is applied alone to square systems, that is to say to systems with as many equations as incognito.The following steps should be continued: First the equation de recurrence is determined. Of the equation i and the incognito iclears. In notation matricial is written: where x is the vector of incognito It takes an approach for the solutions and to this it is designated for 3. You itera in the cycle that changes the approach

5. NUMERICS METHODSLeaving of x=1, y=2 applies two iterations of the Jacobi method to solve the system:

6. NUMERICS METHODSThis Di it is used as unemployment approach in the iterations until Di it is smaller than certain given value.Being Di:

7. NUMERICS METHODSGAUSS-SEIDELGiven a square system of n linear equations with unknown x:Where:

8. NUMERICS METHODSGAUSS-SEIDELThen A can be decomposed into a lower triangular component L*, and a strictly upper triangular component U:The system of linear equations may be rewritten as:

9. NUMERICS METHODSGAUSS-SEIDELThe Gauss–Seidel method is an iterative technique that solves the left hand side of this expression for x, using previous value for x on the right hand side. Analytically, this may be written as:However, by taking advantage of the triangular form of L*, the elements of x(k+1) can be computed sequentially using forward substitution:

10. To solve the following exercise for the method of Gauss-Seidel with an initial value of (0,0,0). Use three iterationsNUMERICS METHODS1ra iteration2da iterationNUMERICS METHODS3ra iterationNUMERICS METHODSGAUSS-SEIDEL RELAXATIONTo solve the previous exercise for the gauss method for relaxation. .Use two iterationsReplacing with the initial values (0,0,0)

11. 1ra iterationNUMERICS METHODS

12. 2da iterationNUMERICS METHODS

13. BIBLIOGRAFIAhttp://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method

14. http://es.wikipedia.org/wiki/M%C3%A9todo_iterativo

15. http://search.conduit.com/Results.aspx?q=METODOS+ITERATIVOS&meta=all&hl=es&gl=co&SearchSourceOrigin=13&SelfSearch=1&ctid=CT2247187NUMERICS METHODS