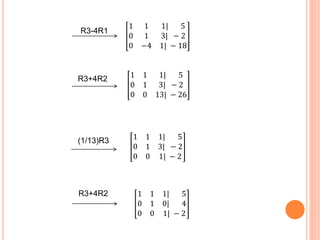
The document discusses the Gauss elimination and Gauss-Jordan methods in linear algebra for solving systems of linear equations. It details the procedures, algorithms, and applications of these methods, including an example involving the extraction of nickel in chemical engineering. Additionally, it contrasts the two methods and explains their historical background and the conditions for applying them.

1. CHEMICAL ENGINEERING
MATHS
(2140505)
GAUSS ELIMINATION AND GAUSS JORDAN METHOD

2. MADE BY:

3. GAUSS ELIMINATION METHOD
 In linear algebra, Gaussian elimination (also known
as row reduction) is an algorithm for solving systems
of linear equations.
 It is usually understood as a sequence of operations
performed on the associated matrix of coefficients.
 This method can also be used to find the rank of a
matrix, to calculate the determinant of a matrix, and to
calculate the inverse of an invertible square matrix.
 The method is named after Carl Friedric Gauss(1777–
1855), although it was known to Chinese
mathematicians as early as 179 AD.

4.  To perform row reduction on a matrix, one uses a
sequence of elementary row operations to modify the
matrix until the lower left-hand corner of the matrix is
filled with zeros, as much as possible. There are three
types of elementary row operations:
 1) Swapping two rows
 2) Multiplying a row by a non-zero number
 3) Adding a multiple of one row to another row.

5. ALGORITHM OF GAUSS ELIMINATION METHOD
 Start
 Declare the variables and read the order of the matrix n.
 Take the coefficients of the linear equation as:
Do for k=1 to n
Do for j=1 to n+1
Read a[k][j] End for j
End for k
 Do for k=1 to n-1
Do for i=k+1 to n
Do for j=k+1 to n+1
a[i][j] = a[i][j] – a[i][k] /a[k][k] * a[k][j] End for j
End for i
End for k
 Compute x[n] = a[n][n+1]/a[n][n]
 Do for k=n-1 to 1
sum = 0
Do for j=k+1 to n
sum = sum + a[k][j] * x[j] End for j
x[k] = 1/a[k][k] * (a[k][n+1] – sum)
End for k
 Display the result x[k]
 Stop

6. AN EXAMPLE OF GAUSS ELIMINATION METHOD OF
CHEMICAL ENGINEERING APPLICATIONS
Example 1
 A liquid-liquid extraction process conducted in the
Electrochemical Materials Laboratory involved the
extraction of nickel from the aqueous phase into an
organic phase. A typical set of experimental data from
the laboratory is given below.
 Ni aqueous phase, 2 , 2.5, 3
 Ni organic phase, 8.57 , 10 , 12
 Assuming g is the amount of Ni in the organic phase
and a is the amount of Ni in the aqueous phase, the
quadratic interpolant that estimates is given by g= x1a2
+ x2a + x3 , where 2 < a < 3
 Find the values of both the using naïve Gauss
elimination.

7.  The solution of x1, x2, x3 is given by
 Forward Elimination of Unknowns
 Since there are three equations, there will be two steps of
forward elimination of unknowns.
 First step
 Divide Row 1 by 4 and then multiply it by 6.25, that is,
multiply Row 1 by .































12
10
57.8
139
15.225.6
124
3
2
1
x
x
x

8. Subtract the result from Row 2 to get
     391.135625.1125.325.65625.11Row 
































12
3906.3
57.8
139
5625.0625.00
124
3
2
1
x
x
x

9.  Second step
 We now divide Row 2 by −0.625 and then multiply it by
−1.5, that is, multiply Row 2 by .
 Subtract the result from Row 3 to get
     1375.835.15.104.22Row 
































855.0
3906.3
57.8
1.000
5625.0625.00
124
3
2
1
x
x
x

10.  Back Substitution
 From the third equation,
Substituting the value of in the second equation,
855.01.0 3 x
1.0
0.855
3 x
55.8
    3906.35625.0625.0 32  xx
 
625.0
5625.03906.3 3
2



x
x
 
625.0
55.85625.03906.3



27.2

11.  Hence the solution vector is
 Hence, g= 1.14a2 - 2.27a +8.55, where g is the amount
of nickel in organic phase and a is the amount of nickel
in aqueous phase.
 Thus, if the value of g is given by 2.3g/l then the value
of a will be , g= 1.14(2.3)2 - 2.27(2.3) + 8.55
= 9.3596 g/l





















55.8
27.2
14.1
3
2
1
x
x
x

12. GAUSS JORDAN METHOD
 Some authors use the term Gaussian
elimination to refer only to the procedure until the
matrix is in echelon form, and use the
term Gauss-Jordan elimination to refer to the
procedure which ends in reduced echelon form.
 In linear algebra, Gauss–Jordan elimination is an
algorithm for getting matrices in reduced row
echelon form using elementary row operations. It
is a variation of Gaussian elimination.

13. HISTORY ABOUT GAUSS JORDAN
METHOD
 it is a variation of Gaussian elimination as
described by Wilhelm Jordan in 1887.
 However, the method also appears in an article
by Clasen published in the same year. Jordan
and Clasen probably discovered Gauss–Jordan
elimination independently.

14. HERE ARE THE STEPS TO GAUSS-JORDAN
ELIMINATION:
 Turn the equations into an augmented matrix.
 Use elementary row operations on matrix [A|b] to
transform A into diagonal form. Make sure there are
no zeros in the diagonal.
 Divide the diagonal element and the right-hand
element (of b) for that diagonal element's row so
that the diagonal element is equal to one.

15. HERE ARE THE STEPS TO GAUSS-JORDAN
ELIMINATION:
 1. Write the augmented matrix of the system.
 2. Use row operations to transform the augmented
matrix in the form described below, which is called
the reduced row echelon form (RREF).
(a) The rows (if any) consisting entirely of zeros are
grouped together at the bottom of the matrix.
(b) In each row that does not consist entirely of
zeros, the leftmost nonzero element is a 1 (called a
leading 1 or a pivot).

16. (c) Each column that contains a leading 1 has
zeros in all other entries.
(d) The leading 1 in any row is to the left of any
leading 1’s in the rows below it.
o 3. Stop process in step 2 if you obtain a row
whose elements are all zeros except the last one
on the right. In that case, the system is
inconsistent and has no solutions. Otherwise,
finish step 2 and read the solutions of the system
from the final matrix.

17. ALGORITHM OF GAUSS JORDAN
METHOD
 Start
 Read the order of matrix ’n’ and read the coefficient of
the linear eq.
 Do for k=1 to n.
Do for l=k+1 to n+1
a[k][l]=a[k][l]/a[k][k] end for l set a[k][k]=1
 Do for i=1 to n.
If (i is not equal to k) then ,
do for j=k+1 to n+1
a[i][j]=a[i][j]-(a[k][j]*a[i][k])
End for j
End for i
End for k.

18.  Do for m=1 to n.
x[m]=a[m][n+1],display x[m],[n] for m
 Stop.

19.  Example 1. Solve the following system by
using the Gauss-Jordan elimination method.
x + y + z = 5
2x + 3y + 5z = 8
4x + 5z = 2

20.  Solution: The augmented matrix of the system is the
following.
1 1 1|5
2 3 5|8
4 0 5|2
 We will now perform row operations until we obtain a matrix
in reduced row echelon form.
1 1 1|5
2 3 5|8
4 0 5|2
1 1 1| 5
0 1 3| − 2
4 0 5| 2

21. 1 1 1| 5
0 1 3| − 2
0 −4 1| − 18
R3-4R1
1 1 1| 5
0 1 3| − 2
0 0 13| − 26
R3+4R2
(1/13)R3 1 1 1| 5
0 1 3| − 2
0 0 1| − 2
R3+4R2 1 1 1| 5
0 1 0| 4
0 0 1| − 2

22. R1-R3
1 1 0| 5
0 1 0| 4
0 0 1| − 2
1 0 0| 3
0 1 0| 4
0 0 1| − 2
 From this final matrix, we can read the solution of the
system. It is
R1-R2