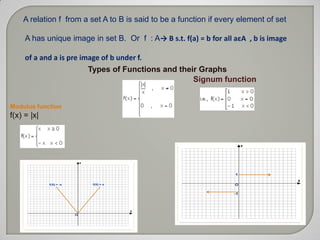
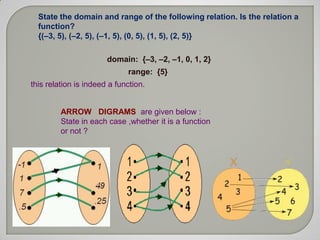
The document discusses Cartesian products, domains, ranges, and co-domains of relations and functions through examples and definitions. It explains that the Cartesian product of sets A and B, written as A×B, is the set of all ordered pairs (a,b) where a is an element of A and b is an element of B. It also defines what constitutes a relation between two sets and provides examples of relations and functions, discussing their domains and ranges. Arrow diagrams are presented to illustrate various functions along with questions and their solutions related to relations and functions.

1. CARTESIAN PRODUCT, DOMAIN, RANGE
,CODOMAIN , ARROW DIAGRAM & GRAPHS.
BY:--INDU THAKUR

2.  We will learn how to link pairs of objects from
two sets and then introduce relations b/w the
two objects in the pair.
 AXB = { (a,b): a ε A, b ε B} for non-empty sets
A,B otherwise AXB=φ, this is the set of all
ordered pairs of elements from A and B.
n(AXB)=n(A)Xn(B)
 AXBXC = {(a,b,c):aεA,bεB,cεC} is called set
of all ordered triplets for non-empty sets.
n(AXBXC) =n(A)Xn(B)Xn(C)
AX(BXC)=(AXB)XC=AXBXC.
 AXB,BXA are not equal (not commutative).

3.  Let P,Q be two sets then a relation R from P to Q is a subset of
PXQ.
 Example: If A={a,b,c,d},B={p,q,r,s},then which of the following are
relations
(i) R1={(a,p),(b,r),(c,s)}
(ii) R2 ={(q,b),(c,s),(d,r)}
 Solution: R1is a relation because R1is the subset of AXB but R2 is
the not the relation of AXB because (q,b)εR2 but not in AXB.(R2 is not a
subset of AXB)
 Total number of relations that can be defined from a set A to B is the
number of possible subsets of AXB.
 If n(A)=P , n(B)=q , then total number of relations is 2pq
OR total number of subsets of AXB.
 Example: If R is relation on a finite set having n elements, then the
number of relations on A is
 Answer 2nxn
 Inverse Function is a relation from B to A defined by
{ (b,a) :(a,b)εR}

4. State the domain and range of the following
relation. Is the relation a function?
{(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}
they gave me two points with the same x-value: (2, –3) and (2,
3). Since x = 2 gives me two possible destinations, then this
relation is not a function.
domain: {2, 3, 4, 6}
range: {–3, –1, 3, 6}
Relations
A relation is a set of inputs and outputs, often
written as ordered pairs (input, output). We can
also represent a relation as a mapping diagram
or a graph. For example, the relation can be
represented as:
* If output has one more unmapped element
say 5 then output becomes codomain then
Range is the subset of codomain
Range ={-2,1,2,4} and Codomain ={-2,1,2.4,5}

5. A relation f from a set A to B is said to be a function if every element of set
A has unique image in set B. Or f : A→ B s.t. f(a) = b for all aεA , b is image
of a and a is pre image of b under f.
Types of Functions and their Graphs
Signum function
Modulus function
f(x) = |x|

6. Reciprocal function f(x) = [x], x εR
is called the smallest
integer function or the
Domain = R – {0} ceiling function.
Range = R – {0} Domain=R , Range =Z.
Square root function
f : R → R (x > 0) such that
Domain =Range is set of all positive
real numbers.

7. State the domain and range of the following relation. Is the relation a
function?
{(–3, 5), (–2, 5), (–1, 5), (0, 5), (1, 5), (2, 5)}
domain: {–3, –2, –1, 0, 1, 2}
range: {5}
this relation is indeed a function.
ARROW DIGRAMS are given below :
State in each case ,whether it is a function
or not ?

8. f : R → R defined by f(x) = x2
Domain = R , Range = *0,∞)
Graph of f : R → R such that f(x) = |x-1|
Graph of f : R → R such that f(x) = |x+1|
Draw a graph of the function defined by f(x) =
Draw a graph of f : R → R defined by f(x) = |x-2|
Ques. If f : R → R Be defined by f(x) = x2 +2x+1 then find
(i) f(-1) x f(1) ,is f(-1)+f(1)=f(0)
(ii) f(2) x f(3) , is f(2) x f(3)=f(6)
Q.1 Find the domain of f(x) = [Hint R-{2,6} ]

9. Ques. Find the domain and Range of following functions:
(i) f(x) =
(ii) f(x) = { ( x, ) : xεR}
Sol. (i) Domain = R , Range = [-1/2 , 1/2+ , y ≠ 0 (How)
Y= it implies yx2 – x + y =0 ,if y=0 then x=0
If y ≠ 0 for x to be real 1 – 4y2 ≥ 0(D≥0)
(ii) Domain = R – {-1,1} , Range = (-∞,0) U [1,∞) ={ y:y<0 or y≥1} (How)
1 –x2 = 1/y it implies x = ± , ≥0 for x to be real.
Find the domain and Range of the function f(x) =
Sol. Domain = R , Range = [1/ 3 , 1] (How)
-1 ≤ sin3x ≤ 1 it implies 1 ≥ sin3x ≥ -1 then 3 ≥ 2- sin3x ≥ 1
1/3 ≤ y 1 by using inequality result ,where y = f(x).

10. A relation R in a set A is called
(i) reflexive, if (a, a) ∈ R, for every a ∈ A,
(ii) symmetric, if (a, b) ∈ R implies that (b, a) ∈ R, for all a, b ∈ A.
(iii) transitive, if (a, b) ∈ R and (b, c) ∈ R implies that (a, c) ∈ R, for
all a, b, c ∈ A.
Example : Let T be the set of all triangles in a plane with R a relation in T given by
R = {(T1, T2) : T1 is congruent to T2}. Show that R is an equivalence relation.
R is reflexive, since every triangle is congruent to itself. Further,(T1, T2) ∈ R
⇒ T1 is congruent to T2 ⇒ T2 is congruent to T1 ⇒ (T2, T1) ∈ R. Hence,R is
symmetric. Moreover, (T1, T2), (T2, T3) ∈ R ⇒ T1 is congruent to T2 and T2
congruent to T3 ⇒ T1 is congruent to T3 ⇒ (T1, T3) ∈ R. Therefore, R is an
equivalence relation.
Example: Let L be the set of all lines in a plane and R be the relation in L defined
as
R = {(L1, L2) : L1 is perpendicular to L2}. Show that R is symmetric but neither
reflexive nor transitive or in other words we can say it is not an equivalence
relation.
If L1 is perpendicular to L2 and L2 is perpendicular to L3, then L1 can
never be perpendicular to L3. In fact, L1 is parallel to L3, i.e., (L1, L2) ∈ R,
(L2, L3) ∈ R but (L1, L3) ∉ R. It is not transitive and cannot be equivalence
relation also.

11. QUESTION BANK WITH HINTS
OF
RELATIONS AND FUNCTIONS
↓
BY:--INDU THAKUR

12. Q.1 The relation R is defined on the set N as R={ (x,x+5) : x <4 ; x,yε N}
Write R in roster form .Write its domain & range.
Q.2 If AXB={(p,q),(p,r),(m,q),(m,r)},find A&B.
Q.3 If A={x,y,z} and B={1,2}.Find the number of relations from A to B.
Q.4 Examine the relation :R={{(2,1),(3,1),(4,1)} and state whether it is a
function or not?
Q.5 Let A={1,2,3,4,5,6,7,8,9,10}.Define a relation R from A to A by R={(x,y):2x –
y=0,where x,y εA}.
Write down its domain ,co-domain & range.
Q.6 Let a relation R1 on the set of real numbers be defined as (a,b)ε R1↔
1+ab>0 for all a,bεR. Show that R1 is reflexive & symmetric but not transitive.
Q.7 If a={1,2,3,4,6}.Let R be the relation on A defined by {(a,b):a,bεA, b is
divisible by a}
Write R in roster form, domain & range of R.
Q.8 If R is a relation from set A={11,12,13} to set B={8,10,12} defined by y=x-3,
then write R-1.
Q.9 Let R be the relation on the set N of natural numbers defined by
R={(a,b):a+3b=12,a,bεN}
Find R, domain of R & range of R.
Q.10 If A={1,2,3},B={1,4,6,9} and R is a relation from A to B defined by ‘x is
greater than y’.Find the range of R.

13. SOLUTIONS:
Ans.1 R={(1,6),(2,7),(3,8)}
domain={1,2,3},range={6,7,8}
Ans .3 22x3 =26
Ans.5 R={(1,2),(2,4),(3,6),(4,8),(5,10)} , Domain= {1,2,3,4,5}
range ={2,4,6,8,10} ,co-domain = A
Ans.6 Reflexive (a,a)εR1 [1+a²>0] & symmetric also as
ab=ba. (1,1/2)εR1,(1/2,-1)ε R1
Ans.7 {(1,1),(1,2)……(1,6),(2,4)….(4,4),(6,6),(3,3),(3,6)} , domain=range
={1,2,3,4,6}
. Ans.8 {8,11),(10.13)}
Ans.9 R={(9,1),(6,2),3,3)}
Ans 10 {1} BY:--INDU THAKUR

14. . Q.1 Find the domain and range of the function f defined by f(x)=
Q.2 Let f(x)=x2 and g(x)=2x+1 be two real functions .Find (f – g)(x),(fg)(x),(f/g)(x)
Q.3 If f={(1,1),(2,3),(o,-1),(-1,-3)} be a linear function from Z into Z . Find f(x).
Q.4 If f(x) = x2 , find
Q.5 Let f(x)= find f(-1) , f(3).
Q.6 If f(x)= x2 – 1/x2 , then find the value of : f(x) +f(1/x)
Q.7 Let A= {-2,-1,0.1,2} and f:A→ Z given by f(x) =x2 – 2x – 3,find range of f and also
pre-image of 6,-3,5.
Q.8 Find the domain and range of real valued function f(x)=
Q.9 Y=f(x)= , then show that x=f(y).
Q.10 If f(x) = , show that f[f(x)].

15. SOLUTIONS :
Ans.1 f(x) is defined real function if 9-x2>0 ,so domain=(-3,3)
and x2=(9 - 1/y2 ) ,x is defined when 9 – 1/y2 ≥0,so range=*1/3,∞)
Ans.2 (f – g)(x)=x2-2x-1, (fg)(x)=2x3+x2 and (f/g)(x)= ,x≠-1/2.
Ans.3 Let f(x)=ax+b be a linear function. If (0,-1),(1,1)εf then we
Can get a=2,b=-1 so linear function becomes f(x)=2x-1
Ans.4 = 2.2
Ans.5 f(-1)=2,f(3)=10.
Ans.6 0
Ans.7 Range of f={0,5,-3,-4} and no pre-image of 6 ;0,2 are the pre-images of -3;-2 is the
pre-image of 5.
Ans.8 It is defined when x ≠4 otherwise it becomes 0/0 form(indeterminate form)
Domain(f)=R-{4}, range (f)={-1} as f(x) =-1 [x-4=-(4-x)]