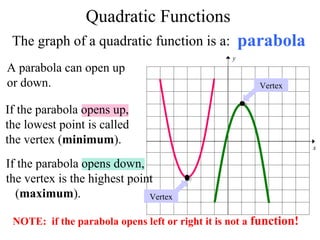
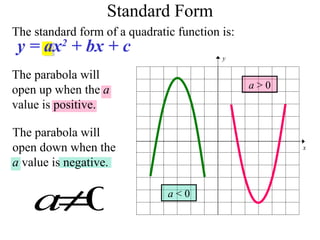
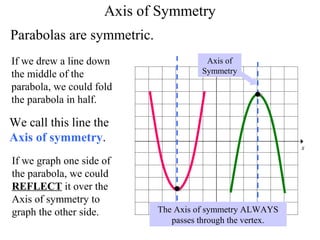
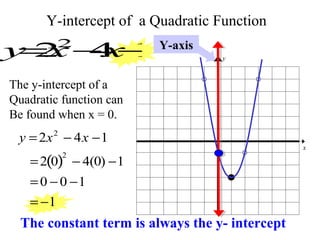
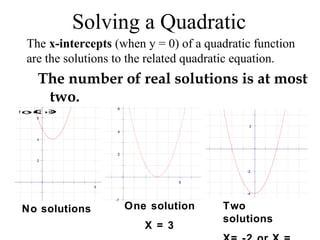
This document provides information about graphing quadratic functions. It defines the standard form of a quadratic function as y = ax^2 + bx + c and explains that the sign of a determines if the parabola opens up or down. It describes how to find the axis of symmetry, vertex, domain and range. The steps to graph a quadratic function are given as finding the axis of symmetry, the vertex, and then two other points to reflect across the axis and connect with a smooth curve. Methods for finding the axis of symmetry, vertex, y-intercept and solutions are demonstrated through examples.

1. Graphing Quadratic Functions
MA.912.A.2.6 Identify and graph functions
MA.912.A.7.6 Identify the axis of symmetry,
vertex, domain, range, and intercept(s) for a
given parabola

2. Quadratic Function
y = ax2 + bx + c
Quadratic Term Linear Term Constant Term
What is the linear term of y = 4x2
– 3? 0x
What is the linear term of y = x2
- 5x ? -5x
What is the constant term of y = x2
– 5x? 0
Can the quadratic term be zero? No!

3. Quadratic Functions
The graph of a quadratic function is a:
A parabola can open up
or down.
If the parabola opens up,
the lowest point is called
the vertex (minimum).
If the parabola opens down,
the vertex is the highest point
(maximum).
NOTE: if the parabola opens left or right it is not a function!
y
x
Vertex
Vertex
parabola

4. y = ax2
+ bx + c
The parabola will
open down when the
a value is negative.
The parabola will
open up when the a
value is positive.
Standard Form
y
x
The standard form of a quadratic function is:
a > 0
a < 0
a≠0

5. y
x
Axis of
Symmetry
Axis of Symmetry
Parabolas are symmetric.
If we drew a line down
the middle of the
parabola, we could fold
the parabola in half.
We call this line the
Axis of symmetry.
The Axis of symmetry ALWAYS
passes through the vertex.
If we graph one side of
the parabola, we could
REFLECT it over the
Axis of symmetry to
graph the other side.

6. Find the Axis of symmetry for y = 3x2
– 18x + 7
Finding the Axis of Symmetry
When a quadratic function is in standard form
the equation of the Axis of symmetry
is
y = ax2
+ bx + c,
2
b
a
x −
=
This is best read as …
‘the opposite of b divided by the quantity of 2 times a.’
( )
18
2 3
x= 18
6
= 3=
The Axis of
symmetry is
x = 3.
a = 3 b = -18

7. Finding the Vertex
The Axis of symmetry always goes through the
_______. Thus, the Axis of symmetry gives
us the ____________ of the vertex.
STEP 1: Find the Axis of symmetry
Vertex
Find the vertex of y = -2x2
+ 8x - 3
2
b
a
x −
= a = -2 b = 8
x=
−8
2(−2)
=
−8
−4
=2
X-coordinate
The x-
coordinate
of the vertex
is 2

8. Finding the Vertex
STEP 1: Find the Axis of symmetry
STEP 2: Substitute the x – value into the original equation
to find the y –coordinate of the vertex.
8 8
2
2 2( 2) 4
b
a
x − − −
= =
− −
= =
The
vertex is
(2 , 5)
Find the vertex of y = -2x2
+ 8x - 3
y = −2 2( )
2
+8 2( )− 3
= −2 4( )+16 − 3
= −8+16 −3
= 5

9. Graphing a Quadratic Function
There are 3 steps to graphing a parabola in
standard form.
STEP 1: Find the Axis of symmetry using:
STEP 2: Find the vertex
STEP 3: Find two other points and reflect them across
the Axis of symmetry. Then connect the five points
with a smooth curve.
MAKE A TABLE
using x – values close to
the Axis of symmetry.
2
b
a
x −
=

10. STEP 1: Find the Axis of
symmetry
( )
4
1
2 2 2
b
x
a
-
= = =
y
x
Graph:y=2x2
−4x−1
Graphing a Quadratic Function
STEP 2: Find the vertex
Substitute in x = 1 to
find the y – value of the
vertex.
( ) ( )2
2 1 4 1 1 3y = - - =- Vertex:1,−3( )
x=1

11. 5
–1
( ) ( )2
2 3 4 3 1 5y = - - =
STEP 3: Find two other
points and reflect them
across the Axis of
symmetry. Then connect
the five points with a
smooth curve.
y
x
( ) ( )2
2 2 4 2 1 1y = - - =-
3
2
yx
Graphing a Quadratic Function
Graph:y=2x2
−4x−1

12. y
x
Y-intercept of a Quadratic Function
y=2x2
−4x−1Y-axis
The y-intercept of a
Quadratic function can
Be found when x = 0.
y =2x2
− 4x −1
=2 0( )2
− 4(0) −1
=0 −0 −1
= −1
The constant term is always the y- intercept

13. The number of real solutions is at most
two.
Solving a Quadratic
No solutions
6
4
2
-2
5
f x()= x2-2 ⋅x( )+5
6
4
2
-2
5
2
-2
-4
-5 5
One solution
X = 3
Two
solutions
The x-intercepts (when y = 0) of a quadratic function
are the solutions to the related quadratic equation.

14. Identifying Solutions
4
2
-2
-4
5
X = 0 or X = 2
Find the solutions of 2x - x2
= 0
The solutions of this
quadratic equation can be
found by looking at the
graph of f(x) = 2x – x2
The x-
intercepts(or
Zero’s) of
f(x)= 2x – x2
are the solutions
to 2x - x2
= 0