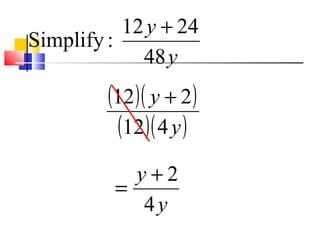This document discusses simplifying rational expressions by dividing out common factors, factoring numerators and denominators, and dividing common factors. It provides examples of simplifying various rational expressions step-by-step and explains how to identify excluded values that would make denominators equal to zero.

1. Rational Expressions
Simplifying
Section 11.3

2. Simplifying Rational Expressions
 The objective is to be able to simplify a
rational expression
5
2x +
3
92
x
x −

3.  Polynomial – The sum or difference of monomials.
 Rational expression – A fraction whose numerator
and denominator are polynomials.
 Reduced form – a rational expression in which the
numerator and denominator have no factors in
common.

4.  Divide out the
common factors
 Factor the
numerator and
denominator and
then divide the
common factors

5. Dividing Out Common Factors
Step 1 – Identify any factors which are common to both the
numerator and the denominator.
5
5 7
x
x( )−
The numerator and denominator have
a common factor.
The common factor is the five.

6. Dividing Out Common Factors
Step 2 – Divide out the common factors.
The fives can be divided since 5/5 = 1
The x remains in the numerator.
The (x-7) remains in the denominator
5
5 7
x
x( )−
=
x
x − 7

7. Factoring the Numerator
and Denominator
Factor the numerator.
Factor the denominator.
Divide out the common factors.
Write in simplified form.
3 9
1 2
2
3
x x
x
+

8. Factoring
Step 1: Look for common factors
to both terms in the numerator.
3 9
1 2
2
3
x x
x
+ ♦3 is a factor of both 3 and 9.
♦X is a factor of both x2
and x.
Step 2: Factor the numerator.
3 9
1 2
2
3
x x
x
+ 3 3
12 3
x x
x
( )+

9. Factoring
Step 3: Look for common factors to the
terms in the denominator and factor.
3 9
1 2
2
3
x x
x
+
The denominator only has one term.
The 12 and x3
can be factored.
The 12 can be factored into 3 x 4.
The x3
can be written as x • x2
.
3 9
1 2
2
3
x x
x
+ 3 3
3 4 2
x x
x x
( )+
• • •

10. Divide and Simplify
Step 4: Divide out the common factors. In this
case, the common factors divide to become 1.
3 3
3 4 2
x x
x x
( )+
• • •
Step 5: Write in simplified form.
x
x
+ 3
4 2

11. You Try It
Simplify the following rational expressions.
1
9
2 4
2
2
.
x y z
x y z
2
3
4 32
.
a
a a
+
+ +
3
3 1 5
7 1 02
.
x
x x
−
− +
4
2 1 5
1 2
2
2
.
x x
x x
− −
− −
5
1 4 3 5 2 1
1 2 3 0 1 8
2
2
.
x x
x x
+ +
+ +

12. Problem 1
9
2 4
2
2
x y z
x y z
= 3 3
3 8
• • • • •
• • • • •
x x y z
x y z z
3
3
• • •
• • •
x y z
x y z
•
3
8
•
•
x
z
1 •
3
8
x
z
=
3
8
x
z
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

13. Problem 2
a
a a
+
+ +
3
4 32 = a
a a
+
+ +
3
3 1( ) ( )
Factor the numerator
and denominator
a
a
+
+
3
3
•
1
1a +
1 •
1
1a +
= 1
1a +
Divide out the
common factors.
Write in simplified
form.
You Try It

14. Problem 3
3 1 5
7 1 02
x
x x
−
− +
= 3 5
5 2
( )
( ) ( )
x
x x
−
− −
x
x
−
−
5
5
•
3
2x −
1 •
3
2x −
=
3
2x −
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.
You Try It

15. Problem 4
You Try It
x x
x x
2
2
2 1 5
1 2
− −
− −
=
( ) ( )
( ) ( )
x x
x x
− +
− +
5 3
4 3
x
x
+
+
3
3
•
x
x
−
−
5
4
1 •
x
x
−
−
5
4
=
x
x
−
−
5
4
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

16. Problem 5
1 4 3 5 2 1
1 2 3 0 1 8
2
2
x x
x x
+ +
+ +
=
7 2 5 3
6 2 6 3
2
2
( )
( )
x x
x x
+ +
+ +
( )
( )
2 5 3
2 6 3
2
2
x x
x x
+ +
+ +
•
7
6
1 •
7
6
=
7
6
You Try It
Factor the numerator
and denominator
Divide out the
common factors.
Write in simplified
form.

17. x
x
5
105
:Simplify
− ( )
x
x
5
25 −
=
Factor
( )
x
x 2−
=
x
x 2−
=

18. 1
23
:Simplify 2
2
−
++
y
yy
( )( )
( )( )11
21
−+
++
yy
yy
1
2
−
+
=
y
y

19. y
y
48
2412
:Simplify
+
( )( )
( )( )y
y
412
212 +
y
y
4
2+
=

20. xx
xx
23
2
:Simplify 2
2
+
+
( ) ( )
( ) ( )
2 1
3 2
x x
x x
+
+
2 1
3 2
x
x
+
=
+

21. 2
2
9
Simplify:
2 15
a
a a
−
+ −
( ) ( )
( ) ( )
3 3
5 3
a a
a a
+ −
+ −
12
1
+
+
=
a
a

22. x
x
−
−
4
4
:Simplify
( )
( )( )41
4
−−
−
x
x
1
1
1
−=
−
=

23. Simplifying
4 3
5 5
x x
x
+
+ 2
5
25
q
q
+
−
3
x
3
5
x
5q +
1
5q −
( )1x +
5 ( )1x + ( )5q + ( )5q −
12.1 – Simplifying Rational Expressions

24. Simplifying
2
2
11 18
2
x x
x x
+ +
+ −
( )2x +
( )
( )
9
1
x
x
+
−
( )9x +
( )2x + ( )1x −
12.1 – Simplifying Rational Expressions

25. Simplifying
4
4
x
x
−
−
4x −
4x −
=
4x− +
1− ( )4x −
1−
12.1 – Simplifying Rational Expressions

26. Restrictions on
Rational Expressions
For what value of x is undefined?x x
x
2
2 1 5
4 2 0
− −
−
It is undefined for any value of “x” which makes the
denominator zero.
4 2 0 0x − =
4 5 0( )x − =
x − =5 0
x − + = +5 5 0 5
x = 5
The restriction is
that x cannot
equal 5.

27. YOU TRY IT
What are the excluded values of the variables for
the following rational expressions?
1
4 2
1 4
3 2
2 3
.
y z
y z
2
3 6
2 1 2
2
.
x
x
−
−
3
4 1 2
2 8
2
2
.
c c
c c
+ −
+ −

28. Problem 1
Solution
y ≠ 0
z ≠ 0

29. Problem 2
Solution
2x - 12 = 0
2x - 12 + 12 = 0 + 12
2x = 12
2x ÷ 2 = 12 ÷ 2
x = 6
ANSWER
x ≠ 6

30. Problem 3
Solution
C2
+ 2C - 8 = 0
(C-2)(C+4) = 0
C-2 = 0 or C + 4 = 0
C-2+2 = 0 + 2 C + 4 - 4 = 0 - 4
C = 2 or C = -4
Answer
C ≠ 2
C ≠ -4