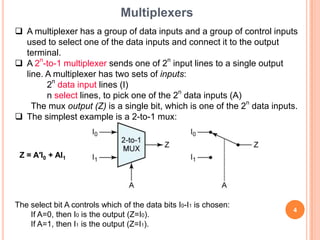
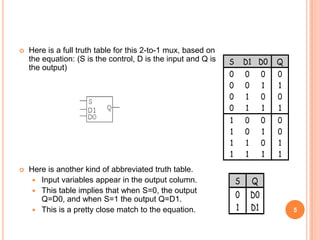
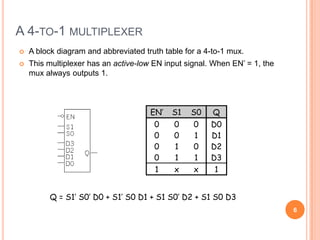
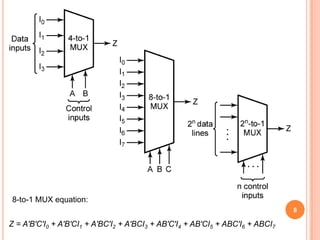
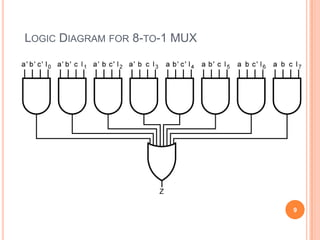
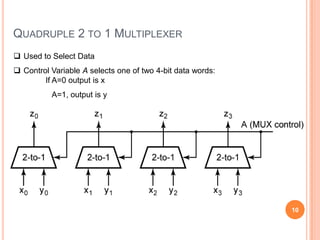
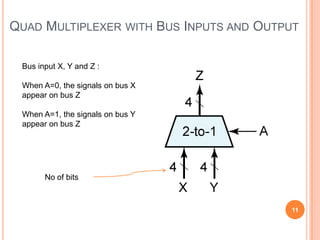
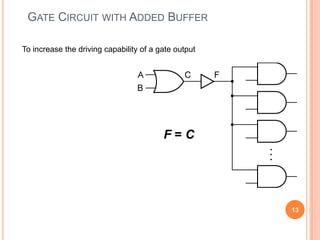
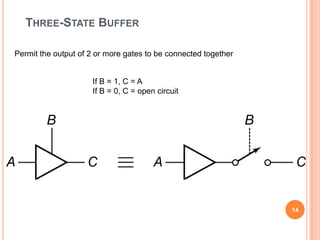
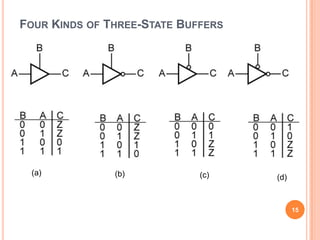
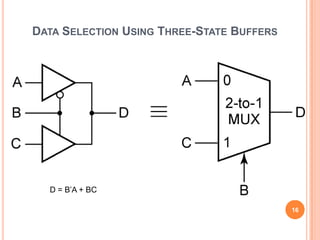
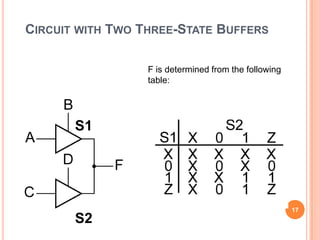
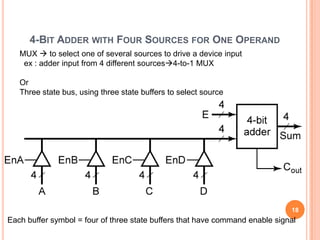
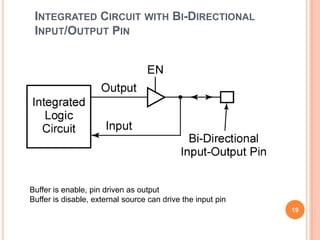
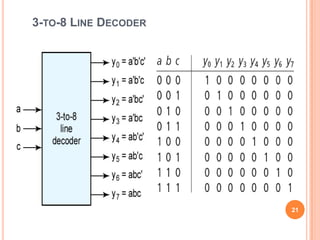
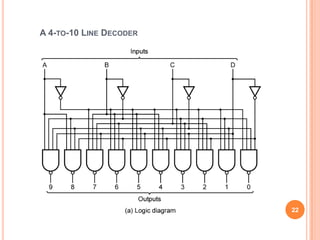
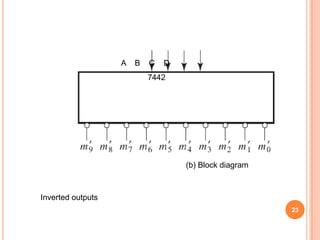
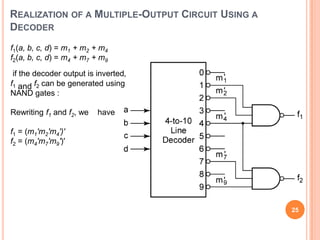
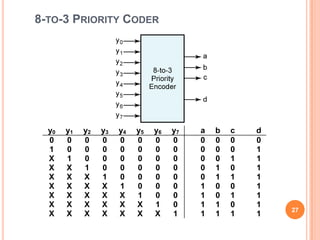
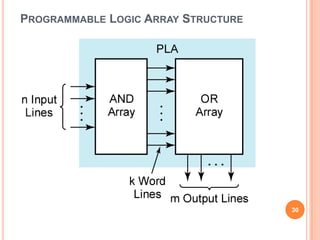
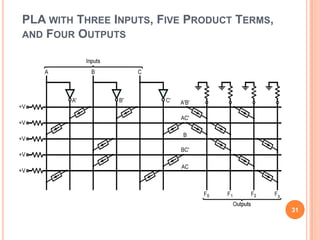
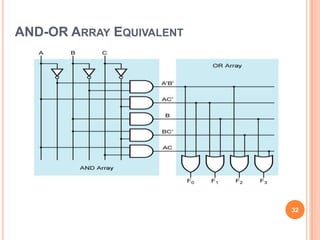
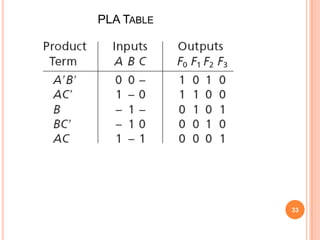
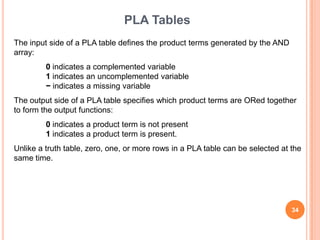
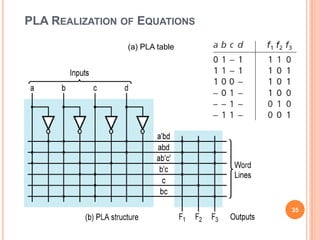
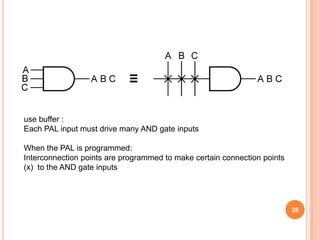
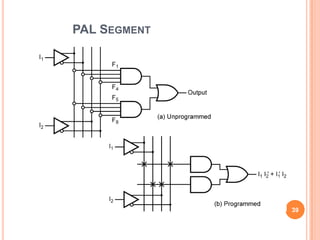
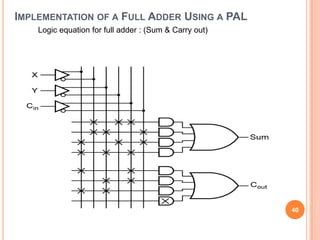
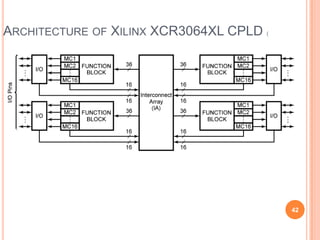
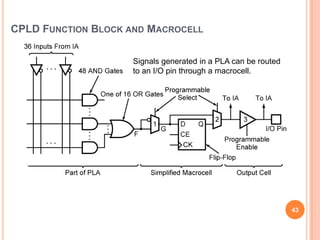
This document discusses complex integrated circuits used in logic design including multiplexers, decoders, and programmable logic devices. It provides details on 4 categories of integrated circuits based on the number of gates - SSI, MSI, LSI, and VLSI. Multiplexers are described as circuits that select one of several data inputs to connect to the output based on the control inputs. Decoders are the inverse, detecting a particular input and activating the corresponding output. Programmable logic devices can be programmed to provide different logic functions, allowing for changes without rewiring the system.

1. KL 2164
DIGITAL ELECTRONICS
Multiplexers, Decoders and
Programmable Logic Devices
Wan Nurdiana Wan Ibrahim

2. COMPLEX INTEGRATED CIRCUIT IN LOGIC DESIGN
4 category of integrated circuit (IC):
1) SSI  small scale integration : NAND, NOR, AND,
OR, Inverter, flip flop
 1 to 4 gates
2) MSImedium scale integration: adder , mux, decoder,
registers, counters
 more complex function
 12 to 100 gates
2

3. 3) LSI  Large scale integration
100 to few thousands gates
4) VLSI very large scale integration
more complex function includes
memories and microprocessor
 several thousands gates
3

4. Multiplexers
 A multiplexer has a group of data inputs and a group of control inputs
used to select one of the data inputs and connect it to the output
terminal.
 A 2n-to-1 multiplexer sends one of 2n input lines to a single output
line. A multiplexer has two sets of inputs:
2n data input lines (I)
n select lines, to pick one of the 2n data inputs (A)
The mux output (Z) is a single bit, which is one of the 2n data inputs.
 The simplest example is a 2-to-1 mux:
Z = A′I0 + AI1
The select bit A controls which of the data bits I0-I1 is chosen:
4
If A=0, then I0 is the output (Z=I0).
If A=1, then I1 is the output (Z=I1).

5.  Here is a full truth table for this 2-to-1 mux, based on
the equation: (S is the control, D is the input and Q is S D1 D0 Q
the output)
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
 Here is another kind of abbreviated truth table.
 Input variables appear in the output column. S Q
 This table implies that when S=0, the output
Q=D0, and when S=1 the output Q=D1. 0 D0
 This is a pretty close match to the equation. 1 D1 5

6. A 4-TO-1 MULTIPLEXER
 A block diagram and abbreviated truth table for a 4-to-1 mux.
 This multiplexer has an active-low EN input signal. When EN’ = 1, the
mux always outputs 1.
EN’ S1 S0 Q
0 0 0 D0
0 0 1 D1
0 1 0 D2
0 1 1 D3
1 x x 1
Q = S1’ S0’ D0 + S1’ S0 D1 + S1 S0’ D2 + S1 S0 D3
6

7. IMPLEMENTING FUNCTIONS WITH MULTIPLEXERS
 Muxes can be used to implement arbitrary functions.
 One way to implement a function of n variables is to use an n-to-1 mux:
 For each minterm mi of the function, connect 1 to mux data input Di.
Each data input corresponds to one row of the truth table.
 Connect the function’s input variables to the mux select inputs. These
are used to indicate a particular input combination.
 For example, let’s look at f(x,y,z) = m(1,2,6,7).
x y z f
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1 7
1 1 1 1

8. 8-to-1 MUX equation:
8
Z = A′B′C′I0 + A′B′CI1 + A′BC′I2 + A′BCI3 + AB′C′I4 + AB′CI5 + ABC′I6 + ABCI7

9. LOGIC DIAGRAM FOR 8-TO-1 MUX
9

10. QUADRUPLE 2 TO 1 MULTIPLEXER
 Used to Select Data
 Control Variable A selects one of two 4-bit data words:
If A=0 output is x
A=1, output is y
10

11. QUAD MULTIPLEXER WITH BUS INPUTS AND OUTPUT
Bus input X, Y and Z :
When A=0, the signals on bus X
appear on bus Z
When A=1, the signals on bus Y
appear on bus Z
No of bits
11

12.  MUX with invert input :
without inversion  active high output
with inversion  active low output
 Additional input “ ENABLE” :
if E=0 (active low) then output is 0
if E=1 (active high) then output function as MUX
12

13. GATE CIRCUIT WITH ADDED BUFFER
To increase the driving capability of a gate output
F=C
13

14. THREE-STATE BUFFER
Permit the output of 2 or more gates to be connected together
If B = 1, C = A
If B = 0, C = open circuit
14

15. FOUR KINDS OF THREE-STATE BUFFERS
(a) (b) (c) (d)
15

16. DATA SELECTION USING THREE-STATE BUFFERS
D = B’A + BC
16

17. CIRCUIT WITH TWO THREE-STATE BUFFERS
F is determined from the following
table:
S1
17
S2

18. 4-BIT ADDER WITH FOUR SOURCES FOR ONE OPERAND
MUX  to select one of several sources to drive a device input
ex : adder input from 4 different sources4-to-1 MUX
Or
Three state bus, using three state buffers to select source
18
Each buffer symbol = four of three state buffers that have command enable signal

19. INTEGRATED CIRCUIT WITH BI-DIRECTIONAL
INPUT/OUTPUT PIN
Buffer is enable, pin driven as output
Buffer is disable, external source can drive the input pin
19

20. Decoders
 In older days, the (good) printers used be like typewriters:
 To print “A”, a wheel turned, brought the “A” key up, which then
was struck on the paper.
 Letters are encoded as 8 bit codes inside the computer.
 When the particular combination of bits that encodes “A” is
detected, we want to activate the output line corresponding to A
 (Not actually how the wheels worked)
 How to do this “detection” : decoder
 General idea: given a k bit input,
 Detect which of the 2^k combinations is represented
 Produce 2^k outputs, only one of which is “1”.
20

21. 3-TO-8 LINE DECODER
21

22. A 4-TO-10 LINE DECODER
22

23. A B C D
7442
(b) Block diagram
Inverted outputs
23

24. 24
(c) Truth Table

25. REALIZATION OF A MULTIPLE-OUTPUT CIRCUIT USING A
DECODER
f1(a, b, c, d) = m1 + m2 + m4
f2(a, b, c, d) = m4 + m7 + m9
if the decoder output is inverted,
f1 and f2 can be generated using
NAND gates :
Rewriting f1 and f2, we have
f1 = (m1′m2′m4′)′
f2 = (m4′m7′m9′)′
25

26. Encoders
 An encoder performs the inverse function of a decoder.
 If input yi is 1 and the other inputs are 0,
 abc outputs represent a binary number equal to i.
For example, if y3 = 1, then abc = 011.
 If more than one input is 1, the highest numbered input determines the output.
 An extra output, d, is 1 if any input is 1, otherwise d is 0.
 This signal is needed to distinguish the case of all 0 inputs from the case
where only y0 is 1.
26

27. 8-TO-3 PRIORITY CODER
y0 y1 y2 y3 y4 y5 y6 y7 a b c d
0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 1
X 1 0 0 0 0 0 0 0 0 1 1
X X 1 0 0 0 0 0 0 1 0 1
X X X 1 0 0 0 0 0 1 1 1
X X X X 1 0 0 0 1 0 0 1
X X X X X 1 0 0 1 0 1 1
X X X X X X 1 0 1 1 0 1
27
X X X X X X X 1 1 1 1 1

28. Programmable Logic Devices
A programmable logic device (or PLD) :
 a general name for a digital integrated circuit
 capable of being programmed to provide a variety of different logic functions
 replace a large number of integrated circuit
digital system is designed using a PLD:
changes in the design can easily be made
 changing the programming of the PLD
 without having to change the wiring in the system
28

29. Programmable Logic Arrays
A programmable logic array (PLA) :
 performs the same basic function as a ROM
 n inputs and m outputs can realize m functions of n variables
The internal organization of the PLA:
 AND array : realizes selected product terms of the input variables
 The OR array : Ors together the product terms needed to form the output
functions
 PLA implements a sum-of-products expression.
29

30. PROGRAMMABLE LOGIC ARRAY STRUCTURE
30

31. PLA WITH THREE INPUTS, FIVE PRODUCT TERMS,
AND FOUR OUTPUTS
31

32. AND-OR ARRAY EQUIVALENT
32

33. PLA TABLE
33

34. PLA Tables
The input side of a PLA table defines the product terms generated by the AND
array:
0 indicates a complemented variable
1 indicates an uncomplemented variable
− indicates a missing variable
The output side of a PLA table specifies which product terms are ORed together
to form the output functions:
0 indicates a product term is not present
1 indicates a product term is present.
Unlike a truth table, zero, one, or more rows in a PLA table can be selected at the
same time.
34

35. PLA REALIZATION OF EQUATIONS
(a) PLA table
35

36. Programmable Array Logic
The PAL (programmable array logic):
 a special case of the PLA
 the AND array is programmable
 the OR array is fixed
Basic structure PAL is same as PLA
PAL is less expensive than PLA :
 only the AND array is programmable
PAL is easier to program
36

37. Buffer logically equivalent to
37

38. use buffer :
Each PAL input must drive many AND gate inputs
When the PAL is programmed:
Interconnection points are programmed to make certain connection points
(x) to the AND gate inputs
38

39. PAL SEGMENT
39

40. IMPLEMENTATION OF A FULL ADDER USING A PAL
Logic equation for full adder : (Sum & Carry out)
40

41. Complex Programmable Logic Devices
As integrated circuit technology continues to improve,;
o more gates can be placed on a single chip
o development of complex programmable logic devices (CPLDs)
Instead of a single PAL or PLA on a chip,
 many PALs or PLAs can be placed on a single CPLD chip and
interconnected.
41

42. ARCHITECTURE OF XILINX XCR3064XL CPLD (
42

43. CPLD FUNCTION BLOCK AND MACROCELL
Signals generated in a PLA can be routed
to an I/O pin through a macrocell.
43