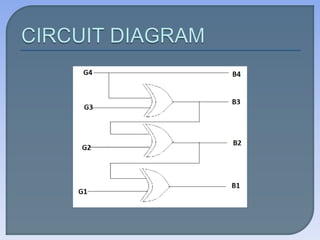
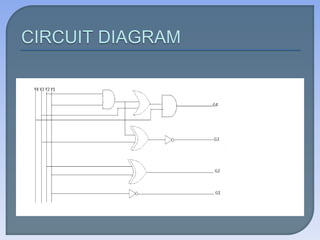
The document explains the difference between analog and digital signals, highlighting that digital signals have two discrete values (high and low), often represented as binary 0 and 1 in various coding systems. It covers binary coding techniques such as BCD, excess-3, and gray code, along with methods for converting between codes and using K-maps for simplifying Boolean expressions. The document further discusses the applications and limitations of these coding systems and provides examples of logical expressions and code representations.

1. BY :-
ALAPAN RANJAN BANERJEE

2. The electronics signals are continuous and
can have any value over a given range,
are called analog signal.
The electrical signal which have only two
discreet value or level (high and low), is
called digital signal. Actual values of the
signal are unimportant.

3.  In this system, if 0 and 1 refer to the low and high
values respectively, the system is termed a
positive logic system.
 On the contrary, if 1 and 0 refer to the low and high
values respectively, the system is termed a
negative logic system.
 The signal between 0 and 1 volt can be recognized
as binary 0, between 3 and 5 volt can be taken as
binary 1. In digital system functions only in two
state, i.e. in a binary manner. The voltage is only
leveled low or high; its exact value is immaterial.

4.  A binary code represents text, computer
processor instructions, or any
other data using a two-symbol system. The
two-symbol system used is often the binary
number system's 0 and 1.
 The binary code assigns a pattern of binary
digits, also known as bits, to each character,
instruction, etc. For example, a
binary string of eight bits can represent any of
256 possible values and can therefore
represent a wide variety of different items.

6. BINARY CODE
NUMERIC CODE
BCD CODE XS-3 CODE GRAY CODE
ALPHANUMERIC
CODE
EBCDIC CODE ASCII CODE

8.  The Binary-coded Decimal uses the binary
number system to specify the decimal
numbers 0 to 9.
 It has four bits. The weights of the first
position is 20 (1), the second 21(2), the third
22(4), and the fourth 23(8). Reading from left to
right, the weights 8-4-2-1, hence it is called
8421 code.
 Valid BCD code are : 0000 to 1001
 Invalid BCD code are :1010 to 1111

9. As the name indicates, the excess-3
represents a decimal number, in binary
form, as a number greater than 3. An
excess-3 code is obtained by adding 3 to a
decimal number.
Valid excess-3 code : 0011 to 1100
Invalid excess-3 code :[0000 to 0010] and
[1101 to 1111]

10.  The Gray Code belongs to a class of code
called minimum-change code, in which only
one bit in the code group changes when
moving from one step to another step.
 The Gray Code is a non-weighted code.
Therefore it is not suitable arithmetic
operations but finds applications in
input/output devices and in some types of
analog to digital converters.

11. A code converters is a logic circuits whose
bit patterns representing numbers (or
characters) in one code and whose
outputs are the corresponding
representations in another code.
Code converters are usually multiple
output circuits.

12.  The K-map method of solving the
logical expressions is referred to
as the graphical technique of
simplifying Boolean expressions.
K-maps are also referred to as 2D
truth tables as each K-map is
nothing but a different format of
representing the values present in
a one-dimensional truth table.
 In K-maps, the rows and the
columns of the table use Gray
code-labeling which in turn
represent the values of the
corresponding input variables. This
means that each K-map cell can
be addressed using a unique Gray
Code-Word

14.  Minterm expansion
will
be ∑m(4,5,7,8,10,11,
13,14) + ∑d (0,1,2)
 Maxterm expansion
will be
∏M(3,6,9,12,15) · ∏D
(0,1,2)

15.  we have to fill the K-
map cells with one for
each minterm, zero
for each maxterm,
and X for Don't Care
terms.
 The procedure is to
be repeated for every
single output variable.

16.  The process has to be initiated by grouping
the bits which lie in adjacent cells such that
the group formed contains the maximum
number of selected bits. This means that for
an n-variable K-map with 2ncells,
The procedure must be applied for all
adjacent cells of the K-map, even when they
appear to be not adjacent—the top row is
considered to be adjacent to the bottom row
and the rightmost column is considered to be
adjacent to the leftmost column
 A bit appearing in one group can be repeated
in another group provided that this leads to
the increase in the resulting group-size.
 Don’t Care conditions are to be considered
for the grouping activity if and only if they
help in obtaining a larger group.
Otherwise, they are to be neglected.

17.  For each of the resulting groups,
we have to obtain the
corresponding logical expression
in terms of the input-variables. This
can be done by expressing the bits
which are common amongst the
Gray code-words which represent
the cells contained within the
considered group.
 Thus, Y =
 B̅ D̅ + A̅ C̅ + A̅ BD + BC̅ D + AB̅ C
+ ACD̅
 OR Y = (A+B) (B+C+D̅ ) (A+C̅ +D)
(A̅ +B̅ +C+D) (A̅ +B̅ +C̅ +D̅ )

20. 4-BIT BINARY 4-BIT GRAY
B4 B3 B2 B1 G4 G3 G2 G1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 1
0 0 1 0
0 1 1 0
0 1 1 1
0 1 0 1
0 1 0 0
1 1 0 0
1 1 0 1
1 1 1 1
1 1 1 0
1 0 1 0
1 0 1 1
1 0 0 1
1 0 0 0

21. FOR G4 (G4=B4)
FOR G3 (G3=
B4.B3+B3.B4
B4⊕B3)
B2B1
B4B3
00 01 11 10
00 0 0 0 0
01 0 0 0 0
11 1 1 1 1
10 1 1 1 1
B2B1
B4B3
00 01 11 10
00 0 0 0 0
01 1 1 1 1
11 0 0 0 0
10 1 1 1 1

22. FOR G2 (G2=B2.B3+B3.B2
B2 ⊕B3)
FOR G1 (G1= B2.B3+B3.B2
B2 ⊕B1)
B2B1
B4B3
00 01 11 10
00 0 0 1 1
01 1 1 0 0
11 1 1 0 0
10 0 0 1 1
B2B1
B4B3
00 01 11 10
00 0 1 0 1
01 0 1 0 1
11 0 1 0 1
10 0 1 0 1

26. 4 BIT GRAY 4 BIT BINARY
G4 G3 G2 G1 B4 B3 B2 B1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 1
0 0 1 0
0 1 1 1
0 1 1 0
0 1 0 0
0 1 0 1
1 1 1 1
1 1 1 0
1 1 0 0
1 1 0 1
1 0 0 0
1 0 0 1
1 0 1 1
1 0 1 0

27. FOR B4 =G4
FOR B3= G4.G3+G3.G4
=G4⊕G3
G2G1
G4G3
00 01 11 10
00 0 0 0 0
01 0 0 0 0
11 1 1 1 1
10 1 1 1 1
G2G1
G4G3
00 01 11 10
00 0 0 0 0
01 1 1 1 1
11 0 0 0 0
10 1 1 1 1

28. FOR B2= G2⊕G3⊕G4 FOR B1=G1⊕G2⊕G3⊕G4
G2G1
G4G3
00 01 11 10
00 0 0 1 1
01 1 1 0 0
11 0 0 1 1
10 1 1 1 1
G2G1
G4G3
00 01 11 10
00 0 1 0 1
01 1 0 1 0
11 0 1 0 1
10 1 0 1 0

32. 4-BIT BINARY 4-BIT BCD
B4 B3 B2 B1 Y4 Y3 Y2 Y1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
X X X X
X X X X
X X X X
X X X X
X X X X
X X X X

33. FOR Y4=B4 FOR Y3=B3
B2B1
B4B3
00 01 11 10
00 0 0 0 0
01 0 0 0 0
11 X X X X
10 1 1 X X
B2B1
B4B3
00 01 11 10
00 0 0 1 1
01 1 1 1 1
11 X X X X
10 0 0 X X

34. FOR Y2=B2 FOR Y1=B1
B2B1
B4B3
00 01 11 10
00 0 0 1 1
01 0 0 1 1
11 X X X X
10 0 0 X X
B2B1
B4B3
00 01 11 10
00 0 1 1 0
01 0 1 1 0
11 X X X X
10 0 1 X X

37. 4-BIT BCD 4-BIT EXCESS-3
B4 B3 B2 B1 Y4 Y3 Y2 Y1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0

38. FOR Y4= B4+B3.B1+B3.B2
FOR
Y3=B3.B1+B3.B2+B3.B2.B1
B2B1
B4B3
00 01 11 10
00 0 0 0 0
01 0 1 1 1
11 X X X X
10 1 1 X X
B2B1
B4B3
00 01 11 10
00 0 1 1 1
01 1 0 0 0
11 X X X X
10 0 1 X X

39. FOR Y2= B2.B1+B2.B1
FOR Y1=B2.B1+B2.B1
=B1
B2B1
B4B3
00 01 11 10
00 1 0 1 0
01 1 0 1 0
11 X X X X
10 1 0 X X
B2B1
B4B3
00 01 11 10
00 1 0 0 1
01 0 0 0 1
11 X X X X
10 1 0 X X

42. 4-BIT EXCESS-3 4-BIT BCD
Y4 Y3 Y2 Y1 B4 B3 B2 B1
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1

43. FOR B4=Y4(Y3+Y2.Y1)
FOR
B3=Y3.Y1+Y3.Y2+Y3.Y2.Y1
=Y3 ⊕Y2.Y1
Y2Y1
Y4Y3
00 01 11 10
00 X X 0 X
01 0 0 0 0
11 1 X X X
10 0 0 1 0
Y2Y1
Y4Y3
00 01 11 10
00 X X 0 X
01 0 0 1 0
11 0 X X X
10 1 1 0 1

44. FOR B2=Y2 ⊕Y1
FOR B1=Y2.Y1+Y2.Y1
=Y1
Y2Y1
Y4Y3
00 01 11 10
00 X X 0 X
01 0 1 0 1
11 X X X X
10 0 1 0 1
Y2Y1
Y4Y3
00 01 11 10
00 X X 0 X
01 1 0 0 1
11 1 X X X
10 1 0 X 1

47.  WEIGHTED AND NON-WEIGHTED CODE
 SEQUEMTIAL CODE
 SELF COMPLEMENTING CODE
 CYCLIC CODE
 REFLECTIVE CODE

49. ASCII CODE
EBCDIC CODE
 The ASCII code- American Standards Code For Information
Interchange is used in most microcomputers by its
manufacturers.
 This code is represented by 7 bit binary combination
 EBDIC or Extended Binary Coded Decimal Interchange Code is
used in IB equipment.
 It differs from ASCII code only in its grouping for the different
alphanumeric characters.
 It uses 8 bits for each characters.