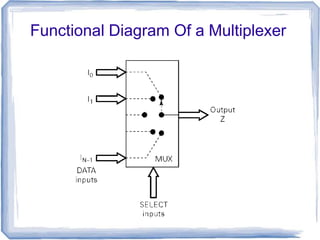
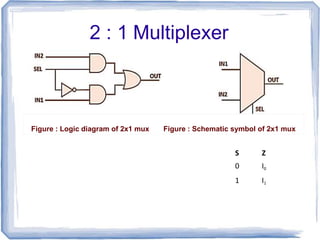
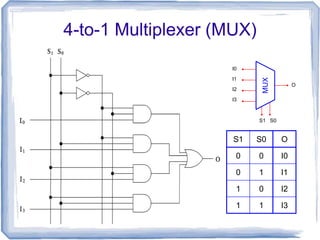
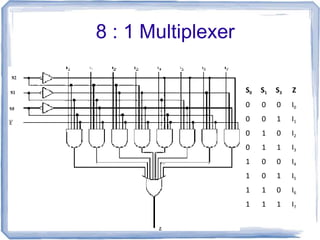
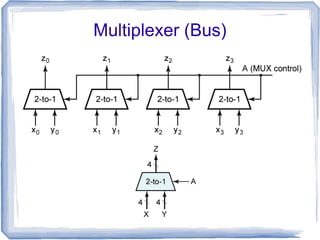
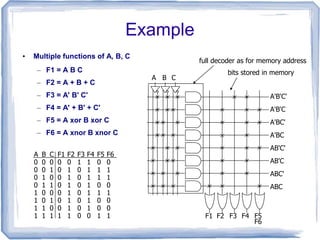
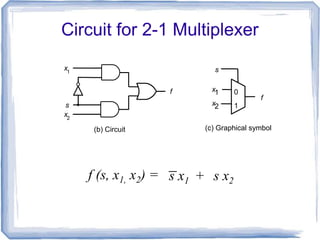
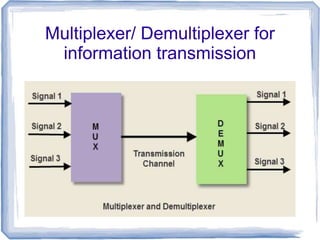
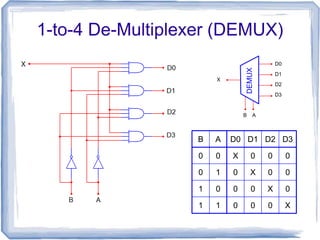
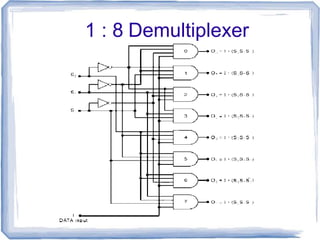
This document discusses multiplexers and demultiplexers. It defines them as devices that allow digital information from several sources to be routed onto a single line (multiplexers) or distributed to multiple output lines (demultiplexers). The key properties of multiplexers and demultiplexers are described, including the relationship between the number of inputs, outputs, and selection lines. Examples of implementing multiplexers and demultiplexers using logic gates are provided.

1. BY UNSA SHAKIR
Multiplexers and
Demultiplexers

2. • Solve by using K-map.
• Design a circuit using logic function.
Exercise:

3. Exercise:
1. Implement the XOR function using only AND
and OR gates
2. Design a circuit using only truth tables and
logic function using AND, OR and NOT gates

4. Multiplexer
(DATA SELECTOR)
A multiplexers (MUX) is a device that allows
digital information from several sources to be
routed onto a single line for transmission over
that line to a common destination.
MUX Types
 2-to-1 (1 select line)
 4-to-1 (2 select lines)
 8-to-1 (3 select lines)
 16-to-1 (4 select lines)

5. Multiplexers
 A multiplexer has
 N control / select inputs
 2N
data inputs
 1 output
 Selection input (N) determines the input that
should be connected to the output

6. Functional Diagram Of a Multiplexer

7. 2 : 1 Multiplexer
S
0
1
Z
I0
I1
Figure : Logic diagram of 2x1 mux Figure : Schematic symbol of 2x1 mux

8. 4-to-1 Multiplexer (MUX)
S1 S0 O
0 0 I0
0 1 I1
1 0 I2
1 1 I3
MUX
I0
I1
I2
I3
O
S1 S0

9. 8 : 1 Multiplexer
S0 S1 S3 Z
0 0 0 I0
0 0 1 I1
0 1 0 I2
0 1 1 I3
1 0 0 I4
1 0 1 I5
1 1 0 I6
1 1 1 I7

10. 8 : 1 Multiplexer

11. ECE 331 - Digital System Design
Multiplexer (Bus)

12. Multiplexers
Exercise:
Design an 8-to-1 multiplexer using
• 4-to-1 multiplexer
• 2-to-1 multiplexer

13. 8-to-1 multiplexer using
4-to-1 multiplexer

14. 8-to-1 multiplexer using
2-to-1 multiplexer

15. 8-to-1 multiplexer using
2-to-1 multiplexer

16. Multiplexers
Exercise:
Design a 16-to-1 multiplexer using
4-to-1 multiplexers only.

17. 16-to-1 multiplexer using
4-to-1 multiplexers

18. • It's often desirable to add an enable input EN to a
multiplexer. An enable input makes the multiplexer operate.
• It is like an on switch of your computer, when you connect
the power supply to cpu it has provision to start functioning.
• A digital logic circuit may have more than 1 enable pins.
• When EN = 0, the output LOW (depending on the specific
device).
• When EN = 1, the multiplexer performs its operation
depending on the selection line.
Enable Input

21. Multiplexers as General Purpose Blocks
2 :1 multiplexer can implement any function of n variables
n-1 control variables; remaining variable is a data input to the mux
n-1
Example:
F(A,B,C) = m0 + m2 + m6 + m7
= A' B' C' + A' B C' + A B C' + A B C
= A' B' (C') + A' B (C') + A B' (0) + A B (1)
8:1
MUX
1
0
1
0
0
0
1
1
0
1
2
3
4
5
6
7 S2 S1 S0
A B C
F
"Lookup Table"
S1 S0
A B
4:1
MUX
0
1
2
3
C
C
0
1
F
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
F
1
0
1
0
0
0
1
1
C
C
0
1

22. Multiplexers
• Efficient implementation:

23. Implementation Of Logic Functions
using Multiplexer
A B C F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
f(a, b, c) = a’b’c + ab
0
1
0
0
0
0
1
1
S2 S1 S0
A B C
F
0
1
2
3 8:1 MUX
4
5
6
7

24. A B C O
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
F
C
0
0
1
C
0
0
1
B C
S S1 0
F
0
1 4:1MUX
2
3
f(a, b, c) = a’b’c + ab

25. A B C D O
0 0 0 0 0
0 0 0 1 1
0 0 1 0 0
0 0 1 1 1
0 1 0 0 1
0 1 0 1 0
0 1 1 0 0
0 1 1 1 0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 1
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 1
F
D
D
D’
0
0
D’
1
1
f(a, b, c) = F= A’B’C’D + A’B’CD + A’BC’D’ + AB’CD
+ ABC’D’ + ABC’D + ABCD’ +ABCD
D
0
1
A B C
S S S2 1 0
F
0
1
2
3 8:1 MUX
4
5
6
7
D’

26. Example
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

27. Example
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1

28. 4-1 Multiplexer (SOP circuit)
f = s1 s0 w0 + s1 s0 w1 + s1 s0 w2 + s1 s0 w3

29. A B C F1 F2 F3 F4 F5 F6
0 0 0 0 0 1 1 0 0
0 0 1 0 1 0 1 1 1
0 1 0 0 1 0 1 1 1
0 1 1 0 1 0 1 0 0
1 0 0 0 1 0 1 1 1
1 0 1 0 1 0 1 0 0
1 1 0 0 1 0 1 0 0
1 1 1 1 1 0 0 1 1
A'B'C'
A'B'C
A'BC'
A'BC
AB'C'
AB'C
ABC'
ABC
A B C
F1 F2 F3 F4 F5
F6
full decoder as for memory address
bits stored in memory
Example
• Multiple functions of A, B, C
– F1 = A B C
– F2 = A + B + C
– F3 = A' B' C'
– F4 = A' + B' + C'
– F5 = A xor B xor C
– F6 = A xnor B xnor C

30. Truth Table for a 2-1 Multiplexer

31. Let’s Derive the SOP form
s x1 x2
s x1 x2
s x1 x2
s x1 x2
f (s, x1, x2) = s x1 x2 s x1 x2 s x1 x2 s x1 x2+ + +

32. Let’s simplify this expression
f (s, x1, x2) = s x1 x2 s x1 x2 s x1 x2 s x1 x2+ + +
f (s, x1, x2) = s x1 (x2 + x2) s (x1 +x1 )x2+ +
f (s, x1, x2) = s x1 s x2+

33. Circuit for 2-1 Multiplexer
f
x1
x2
s
f
s
x1
x2
0
1
(c) Graphical symbol(b) Circuit
f (s, x1, x2) = s x1 s x2+

34. Demultiplexers
(Data Distributor)
A DEMULTIPLEXER (DEMUX) basically
reverses the multiplexing function. It
takes data from one line and distributes
them to a given number of output lines.

35. Demultiplexers
 A demultiplexer has
 N control inputs
 1 data input
 2N
outputs
 A demultiplexer routes (or connects) the data input to
the selected output.
 The value of the control inputs determines the output
that is selected.
 A demultiplexer performs the opposite function of a
multiplexer.

36. Multiplexer/ Demultiplexer for
information transmission

37. Functional Diagram Of a
Demultiplexer

38. Demultiplexers
A B W X Y Z
0 0 I 0 0 0
0 1 0 I 0 0
1 0 0 0 I 0
1 1 0 0 0 I
W = A'.B'
X = A.B'
Y = A'.B
Z = A.B
Out0
In
S1 S0
I
W
X
Y
Z
A B
Out1
Out2
Out3

39. 1 : 2 Demultiplexer
S0 Y0 Y1
0 D 0
1 0 D

40. 1-to-4 De-Multiplexer (DEMUX)
B A D0 D1 D2 D3
0 0 X 0 0 0
0 1 0 X 0 0
1 0 0 0 X 0
1 1 0 0 0 X
D0
D1
D2
D3
X
B A
DEMUX

41. 1 : 8 Demultiplexer

42. 1 : 8 Demultiplexer (Truth Table)
S0 S1 S3 D0 D1 D2 D3 D4 D5 D6 D7
0 0 0 D 0 0 0 0 0 0 0
0 0 1 0 D 0 0 0 0 0 0
0 1 0 0 0 D 0 0 0 0 0
0 1 1 0 0 0 D 0 0 0 0
1 0 0 0 0 0 0 D 0 0 0
1 0 1 0 0 0 0 0 D 0 0
1 1 0 0 0 0 0 0 0 D 0
1 1 1 0 0 0 0 0 0 0 D

43. F1
F2
F3
Demultiplexers as General-purpose
Logic
• F1 = A' B C' D + A' B' C D + A B C D
• F2 = A B C' D’ + A B C
• F3 = (A' + B' + C' + D')
A B
0 A'B'C'D'
1 A'B'C'D
2 A'B'CD'
3 A'B'CD
4 A'BC'D'
5 A'BC'D
6 A'BCD'
7 A'BCD
8 AB'C'D'
9 AB'C'D
10 AB'CD'
11 AB'CD
12 ABC'D'
13 ABC'D
14 ABCD'
15 ABCD
4:16
DECEnable
C D