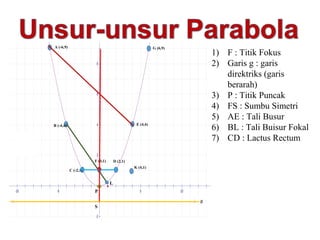
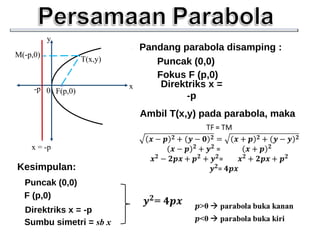
Dokumen tersebut memberikan penjelasan mengenai konsep-konsep dasar parabola seperti titik puncak, titik fokus, direktriks, dan sumbu simetri. Juga dijelaskan cara menentukan persamaan parabola dari informasi geometrisnya seperti titik puncak dan fokus. Contoh soal juga diberikan beserta penyelesaiannya untuk latihan.

1. IIRRIISSAANN KKEERRUUCCUUTT

2. PPAARRAABBOOLLAA
Himpunan titik-titik / tempat kedudukan titik-titik
yang berjarak sama terhadap sebuah titik
tertentu dan sebuah garis lurus tertentu

3. 8
6
4
2
f(x) =
1
4 ( )×x2
-10 -5 5 10
-2
h(x) = -1
A (-6,9)
B (-4,4)
C (-2,1)
D (2,1)
E (4,4)
G (6,9)
F (0,1)
K (4,1)
g
1) F : Titik Fokus
2) Garis g : garis
direktriks (garis
berarah)
3) P : Titik Puncak
4) FS : Sumbu Simetri
5) AE : Tali Busur
6) BL : Tali Buisur Fokal
7) CD : Lactus Rectum
L
P
S

4. Pandang parabola disamping :
Puncak (0,0)
Fokus F (p,0)
Direktriks x =
-p
Ambil T(x,y) pada parabola, maka
y
M(-p,0) T(x,y)
-p x
0 F(p,0)
x = -p
Kesimpulan:
Puncak (0,0)
F (p,0)
Direktriks x = -p
Sumbu simetri = sb x

6. Persamaan parabola berpuncak P(a,b)
Parabola yang dinyatakan oleh persamaan y2 = 4px dengan puncak O(0,0)
digeser ke titik P (a,b) dan sumbu simetrinya tetap sejajar.
•
• a. Titik puncak P(a,b)
• x
O(0,0) F(•p,0)
•
• •
•
y
P(a,b)
F(a+p,b)
a
•
b. Titik fokus F(a + p,b)
c. Direktriks : x = a – p
d. Sumbu simetri : y = b
(y – b)2 = 4p(x – a)
b
x = a - p
-p p
y = b

7. Bila parabola yang dinyatakan oleh x2 = 4py dengan puncak O(0,0)
digeser ke titik P(a,b) dan sumbu simetri tetap sejajar.
Dengan uraian yang sama diperoleh persamaan parabola itu :
(x – a)2 = 4p(y – b)
a. Titik puncak P(a,b)
b. Titik Fokus (a,b + p)
c. Direktriks : y = b – p
d. Sumbu simetri : x = a
p > 0 parabola buka atas
p < 0 parabola buka bawah

8. CONTOH SOAL :
Diberikan persamaan parabola 3x – y2 + 4y + 8= 0
Tentukan : a. Titik puncak c. Direktriks
b. Titik fokus d. Sumbu simetri
Jawab:
Ubah persamaan parabola ke persamaan umum:
3x – y2 + 4y + 8= 0
y2 - 4y = 3x + 8
y2 - 4y + 4 = 3x + 8 + 4
(y – 2)2 = 3x + 12
(y – 2)2 = 3(x + 4)
Didapat persamaan parabola (y – 2)2 = 3(x + 4) yaitu
parabola mendatar yang terbuka ke kanan.

9. Dari persamaan tersebut diperoleh:
a. Titik puncak P(-4,2)
b. 4p = 3 maka p =
3
4
Titik Fokus F(a+p,b)
F(-4 + 3
,2)
4
F(-3 1
,2)
4
c. Persamaan direktriks :
x p a
= - + = - -
x
4 3
4
4
3
4
= -
d. Sumbu simetrinya : y = 2
O(0,0) y
P(-4,2)
F
y

10. LATIHAN SOAL:
a.Tentukan persamaan parabola
yang berpuncak di P(2,4) dan
fokusnya F(-3,4)
b.Tentukan persamaan Parabola
yang titik fokusnya F(2,-3) dan
persamaan direktriksnya y = 5

11. Persamaan Garis Singgung Parabola
n
m
m

12. m