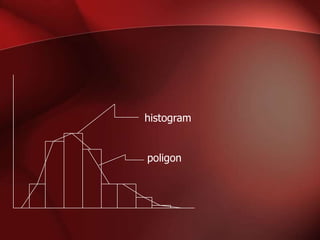
Dokumen tersebut membahas tentang distribusi frekuensi, yang merupakan susunan data menurut kelas interval tertentu beserta frekuensinya. Terdapat penjelasan mengenai bagian-bagian distribusi frekuensi seperti kelas, batas kelas, dan frekuensi kelas, beserta cara penyusunannya melalui contoh soal lengkap. Juga dibahas mengenai histogram sebagai grafik dari tabel frekuensi dan poligon untuk menghubungkan titik tengah

1. Distribusi Frekuensi

2. Pengertian
• Susunan data menurut kelas-kelas interval
tertentu atau menurut kategori tertentu
dalam sebuah daftar
• Dari distribusi frekuensi dapat diperoleh
keterangan atau gambaran sederhana dan
sistematis dari data yang diperoleh.

3. Bagian-bagian distribusi frekuensi
•
•
•
•
Kelas-kelas (class)
Batas kelas (class limits)
Tepi kelas (class boundary)
Titik tengah kelas/tanda kelas (class
mid point/class marks)
• Interval kelas (class interval)
• Panjang Interval kelas atau kelas
(interval kelas)
• Frekuensi kelas (class frequency)

4. Contoh :
Modal (jutaan Rp)
Frekuensi (f)
50-59
16
60-69
32
70-79
20
80-89
17
90-99
15
Jumlah
100
Dari distribusi frekuensi di atas:
1. Banyaknya kelas adalah 5.
2. Batas kelas-kelas adalah 50, 59, 60, 69,…
3. Batas bawah kelas-kelas adalah 50, 60, 70,…
4. Batas atas kelas-kelas adalah 59, 69, 79,…
5. Batas nyata kelas-kelas adalah 49.5, 59.5, 69.5,…
6. Tepi bawah kelas-kelas adalah 49.5, 59.5, 69.5,…
7. Tepi atas kelas-kelas adalah 59.5, 69.5, 79.5,…
8. Titik tengah kelas-kelas adalah 54.4, 64.5, 75.5,…
9. Interval kelas-kelas adalah 50-59, 60-69, 70-79,…
10.Panjang interval kelas-kelas adalah 10.
11.Frekuensi kelas-kelas adalah 16, 32, 20,…

5. Penyusunan Distribusi Frekuensi
1. Mengurutkan data dari yang terkecil ke yang terbesar.
2. Menentukan jangkauan (range) dari data.
Jangkauan = data terbesar – data terkecil
3. Menentukan banyaknya kelas (k).
k = 1 + 3.3 log n;
k Є bulat
ket :
k = banyaknya kelas
n = banyaknya data
Hasil dibulatkan, biasanya ke atas.
4. Menentukan panjang interval kelas.
Panjang interval kelas (i) = jangkauan (R) / banyaknya kelas (k)
5. Menentukan batas bawah kelas pertama.
6. Menuliskan frekuensi kelas secara melidi dalam kolom turus sesuai
banyaknya data.

6. Contoh soal :
Dari hasil pengukuran diameter pipa-pipa yang dibuat oleh sebuah mesin
(dalam mm terdekat), diperoleh data sebagai berikut :
78
72
74
79
74
71
75
74
72
68
72
73
72
74
75
74
73
74
65
72
66
75
80
69
82
73
74
72
79
71
70
75
71
70
70
70
75
76
77
67
Buatlah distribusi frekuensi dari data tersebut!
Penyelesaian :
a. Urutan data:
65
66
67
68
69
70
70
70
70
71
71
71
72
72
72
72
72
72
73
73
73
74
74
74
74
74
74
74
75
75
75
75
75
76
77
78
79
79
80
82
b. Jangkauan (R) = 82 – 65 =17
c. Banyaknya kelas (k) adalah k = 1 + 3.3 log 40
= 1 + 5.3 = 6.3 ≈ 6

7. d. Panjang interval kelas (i) adalah
i = 17/6 =2.8 ≈ 3
e. Batas kelas pertama adalah 65 (data terkecil)
f. Tabel :
Diameter
Turus
Frekuensi
65 – 67
III
3
68 – 70
IIIII I
6
71 – 73
IIIII IIIII II
12
74 – 76
IIIII IIIII III
13
77 – 79
IIII
4
80 – 82
II
2
Jumlah
40

8. histogram
poligon

9. • Histogram adalah grafik dari tabel
frekuensi. Hampir sama bentuk-nya
dengan diagram batang (bar chart);
panjang masing-masing batangnya
ditentukan oleh frekuensinya
• Poligon adalah garis yang
menghubungkan titik tengah puncak
histogram. Manfaatnya untuk
mengetahui bentuk kurva hasil suatu
observasi