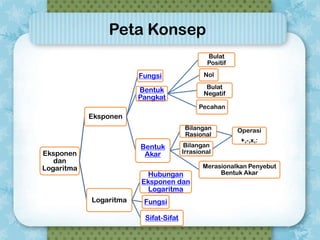
Dokumen ini membahas kompetensi dasar yang harus dicapai siswa setelah mempelajari eksponen dan logaritma, termasuk penerapan disiplin dan tanggung jawab dalam kehidupan sehari-hari. Selain itu, siswa diharapkan dapat menyelesaikan masalah nyata dengan menggunakan eksponen dan logaritma serta memahami sifat-sifat matematis yang terkait. Poin-poin penting juga mencakup berbagai sifat fungsi eksponen dan logaritma serta operasi pada bentuk akar.

3. Kompetensi Dasar
Setelah mengikuti pembelajaran eksponen dan logaritma siswa mampu:
1. Menghayati pola hidup disiplin, kritis, bertanggung jawab, konsisten, dan jujur
serta menerapkannya dalam kehidupan sehari-hari;
2. Memilih dan menerapkan aturan eksponen dan logaritma sesuai dengan
karakteristik
permasalahan
yang
akan
diselesaikan
dan
memeriksa
kebenaran langkah-langkahnya;
3. Menyajikan masalah nyata menggunakan operasi aljabar berupa eksponen
dan logaritma serta menyelesaikannya menggunakan sifat-sifat dan aturan
yang telah terbukti kebenarannya.

4. Pengalaman Belajar
Melalui pembelajaran materi eksponen dan logaritma, siswa memperoleh pengalaman belajar:
•
Mengkomunikasikan karakteristik masalah otentik yang pemecahannya terkait eksponen
dan logaritma;
•
Merancang model Matematika dari sebuah permasalahan autentik yang berkaitan dengan
eksponen dan logaritma;
•
Menyelesaikan model Matematika untuk memperoleh solusi permasalahan yang diberikan;
•
Menafsirkan hasil pemecahan masalah;
•
Membuktikan berbagai sifat terkait eksponen dan logaritma;
•
Menuliskan dengan kata-katanya sendiri konsep persamaan kuadrat berdasarkan ciri-ciri
yang dituliskan sebelumnya;
•
Membuktikan sifat-sifat dan aturan matematika yang berkaitan dengan eksponen dan
logaritma berdasarkan konsep yang sudah dimiliki;
•
Menerapkan berbagai sifat eksponen dan logaritma dalam pemecahan masalah.

5. Peta Konsep
Bulat
Positif
Fungsi
Nol
Bentuk
Pangkat
Bulat
Negatif
Pecahan
Eksponen
Bilangan
Rasional
Bentuk
Akar
Eksponen
dan
Logaritma
Bilangan
Irrasional
Hubungan
Eksponen dan
Logaritma
Logaritma
Fungsi
Sifat-Sifat
Operasi
+,-,x,:
Merasionalkan Penyebut
Bentuk Akar

6. EKSPONEN
 Fungsi Eksponen
Perhatikan tabel berikut! Ada beberapa sifat grafik fungsi eksponen!
x
-3
-2
-1
0
1
2
3
4
f(x) = 2x
⅛
⅟4
⅟2
1
2
4
8
16
f(x) = 2-x
8
4
2
1
⅟2
⅟4
⅛
⅟16
f(x) = 3x
⅟27
⅟9
⅟3
1
3
9
27
81
f(x) = 3-x
27
9
3
1
⅟3
⅟9
⅟27
⅟81
Sifat-sifat tersebut adalah sebagai berikut:
1. Jika x negatif dan rumus fungsi dengan pangkat positif = hasilnya adalah pecahan
2. Jika x positif dan rumus fungsi dengan pangkat positif = hasilnya adalah positif
3. Jika x negatif dan rumus fungsi dengan pangkat negatif = hasilnya adalah positif
4. Jika x positif dan rumus fungsi dengan pangkat negatif = hasilnya adalah pecahan
5. Jika x nol dan rumus fungsi dengan pangkat positif/negatif = hasilnya adalah satu

7.  Bentuk Pangkat
 Pangkat Bulat Positif
Y-Values
Misal: a = bilangan real; n = bilangan bulat positif; maka:
12:00
an = a x a x a x…x a
n faktor
0:00
Artinya: bilangan a dikalikan sebanyak n faktor; dengan a sebagai basis, dan n
sebagai pangkat, maka dihasilkan an 12:00
Contoh:
1. 22
2. 35
3. -24
4. (-5)2
Y-Values
0:00
=2x2=4
= 3 x 3 x 3 x 3 x 3 = 243
= - (2 x 2 x 2 x 2) = -16
12:00
= (-5 x -5) = 25
0:00
-4
-3
-2
-1
0
1
2

8. • Sifat-Sifat Pangkat Bulat Positif
1. am x an = am+n
Dimana; a bilangan real, m dan n bilangan bulat positif
- Bukti:
am x an = a x a x a x…x a x a x a x a x…x a
m faktor
=axaxaxaxa
m+n
= am+n
- Contoh:
1. 53 x 52 = 53+2
= 55
= 3125
2. 92 x 272 = (32)2 x (33)2
= 34 x 36
= 34+6
= 310
= 59049
n faktor

9. 2. am : an = am-n
Dimana; a bilangan real, m dan n bilangan bulat positif
- Bukti:
am : an = a x a x a x…x a : a x a x a x…x a
m faktor
n faktor
=axaxaxaxa
m-n
= am-n
- Contoh:
1. 35 : 32
2. 23 : 8
3. 22 : 42
= 35-2
= 33
= 27
= 23-3
= 20 = 1
= 22 : (22)2
= 22-4 = 2-2
= ⅟4

10. 3. (am)n = amxn
Dimana; a bilangan real, m dan n bilangan bulat positif
- Bukti:
(am)n
= am x am x am…x am
n faktor
= a x a x a…x a a x a x a…x a
m faktor
m faktor
a x a x a…x a … a x a x a…x a
m faktor
n faktor
= a x a x a…x a
mxn
- Contoh:
1. (2x8⅓)2
= (21+1)2
= (22)2
= 24
= 16
=
amxn
m faktor

11.  Pangkat Nol
Diperoleh dari sifat am:an=am-n, jika a bilangan real, m dan n bilangan bulat
positif, dan m = n.
- Bukti :
25 : 2 5 = 2 x 2 x 2 x 2 x 2
=1
2x2x2x2x2
Jadi, a0 = 1
 Pangkat Bulat Negatif
Perhatikan pola pemangkatan berikut ini!
22 = 4
2-1 = ⅟2
21 = 2
2-2 = ⅟4
20 = 1
dst…
Jadi, a-n= 1
a
n
- Bukti : a-n= 1
a
n
=
1
= 1n
a x a x a x…x a
a
n faktor

12.  Pangkat Pecahan
- Misal: a bilangan bulat dan a ≠ 0; m dan n bilangan bulat positif,
Maka:
Contoh:
- Misal: a bilangan bulat dan a ≠ 0; m dan n bilangan bulat positif,
Maka:
Contoh:

13. • Sifat-Sifat Pangkat Pecahan
1.
- Misal: a bilangan bulat dan a > 0,
- Contoh:
dan
adalah pecahan, n ≠ 0.
2.
- Misal: a bilangan bulat dan a > 0,
- Contoh:
dan
adalah pecahan, n ≠ 0.

15. •
Sederhanakanlah operasi pemangkatan
berikut ini!
1.)
4.)
2.)
5.)
3.)

16.  Bentuk Akar
Sebelum mempelajari bentuk akar, terlebih dahulu mengetahui konsep:
• Bilangan Rasional
Adalah bilangan yang dapat dinyatakan dalam bentuk , dengan a dan b bilangan
bulat dan b ≠ 0.
-Contoh : ¼, ½, ¾, 2, 3, , dll.
• Bilangan Irrasional
Adalah bilangan yang tidak dapat dinyatakan dalam bentuk pecahan, dan mengandung
bentuk desimal yang tak terhingga dan tak berpola.
-Contoh: ,
,
, dll.
Bilangan Irrasional yang menggunakan tanda akar ( ) dinamakan bentuk akar.
Namun, tidak semua bilangan yang berada dalam tanda akar merupakan bentuk akar.
Contoh:
= bukan bentuk akar, karena
= 2.
= bentuk akar

17.  Operasi pada Bentuk Akar
• Penjumlahan dan Pengurangan
Dimana, p,q,r bilangan real dan r ≥ 0; maka berlaku:
• Perkalian dan Pembagian
Beberapa sifat perkalian dan pembagian pada bentuk akar adalah sebagai berikut:
-Perkalian:
-Pembagian:

18.  Merasionalkan Penyebut Bentuk Akar
Pada prinsipnya, cara merasionalkan penyebut bentuk akar suatu pecahan adalah
dengan mengalikannya dengan bentuk akar sekawannya.
1. Merasionalkan bentuk
Caranya dengan mengalikan
Jadi:
2. Merasionalkan bentuk
Bilangan sekawan dari
Jadi:
dan
adalah
, dan sebaliknya

19. 3. Merasionalkan bentuk
Bentuk
dan
dan
saling sekawan
Jadi:
4. Menyederhanakan bentuk
Coba perhatikan proses berikut ini!

20. Jadi:

21. Contoh Soal:
• Penjumlahan dan Pengurangan
1.
2.
• Perkalian dan Pembagian
1.
2.
• Merasionalkan
1.

24. •
Carilah hasil dari operasi pengakaran
berikut ini!
• Rasionalkan penyebut pecahan berikut ini!
3.)
1.)
• Tentukan nilai
4.)
2.)
• Sederhanakan bentuk akar berikut ini!
5.)

26. LOGARITMA
 Hubungan Eksponen dan Logaritma
Logaritma pada hakekatnya merupakan kebalikan dari proses pemangkatan
dan/atau pengakaran.
Bentuk Pangkat
Bentuk Akar
Bentuk Logaritma
ax
x
a
m
Unsur Logaritma:
a
log m
x
= Basis
= Numerus
= Hasil Logaritma
m
a
log m
x

27.  Fungsi Logaritma
Perhatikan tabel berikut! Ada beberapa sifat grafik fungsi logaritma!
x
1
2
3
4
8
9
f(x) = 2log x
-1
-1,5
-2
0
1
1,5
2
3
3,15
f(x) = log x
1
1,5
2
0
-1
-1,5
-2
-3
-3,15
f(x) = 3log x
-0,5
-1
-1,25
0
0,5
1
1,25
1,9
2
f(x) = log x
0,5
1
1,25
0
-0,5
-1
-1,25
-1,9
-2
Sifat-sifat tersebut antara lain:
1.
Jika x pecahan dan rumus fungsi dengan basis bilangan bulat positif, hasil = negatif
2.
Jika x bilangan bulat positif > 1 dengan rumus fungsi dengan basis bilangan bulat positif, hasil
= positif
3.
Jika x pecahan dan rumus fungsi dengan basis pecahan, hasil = positif
4.
Jika x bilangan bulat positif > 1 dengan rumus fungsi dengan basis pecahan, hasil = positif
5.
Jika x=1 dengan rumus fungsi dengan basis bilangan bulat positif / pecahan, hasil = nol

28.  Sifat-Sifat Logaritma
1. a log x 1
6. a log m n
n a log m
c
a
2. log 1 0
3. a log x a
7. log m
a
4. log mn
m
5. log
n
8. a log m.m log b
a
a
a
log m
c
log n
a
a
log m
log m
a
a
log n
log n
9.
ab
log m
n
n
m
1
m
log a
a
a
log b
log m

30. • Hitunglah nilai dari :
1.)
• Sederhanakan
4.)
2.)
5.)
3.)