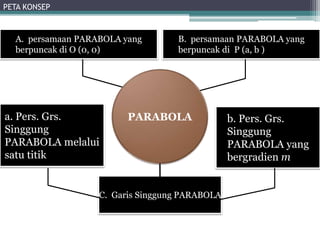
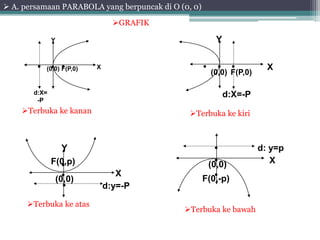
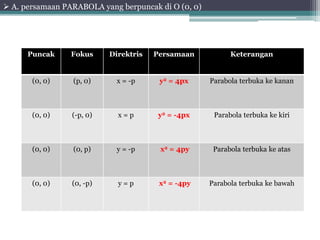
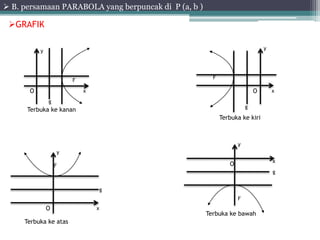
Dokumen tersebut membahas tentang pengertian dan konsep parabola. Terdapat beberapa poin penting yaitu: (1) Persamaan parabola yang berpuncak di titik tertentu dan garis fokus, direktris, sumbu simetrinya. (2) Persamaan garis singgung parabola di satu titik dan yang memiliki gradien tertentu. (3) Contoh soal dan penyelesaiannya.

1. PARABOLA

3. A. persamaan PARABOLA yang
berpuncak di O (0, 0)
B. persamaan PARABOLA yang
berpuncak di P (a, b )
PARABOLA
a. Pers. Grs.
Singgung
PARABOLA melalui
satu titik
C. Garis Singgung PARABOLA
b. Pers. Grs.
Singgung
PARABOLA yang
bergradien m
PETA KONSEP

4. Parabola adalah tempat
kedudukan titik-titik pada
bidang datar yang mempunyai
jarak yang sama terhadap
suatu titik tertentu dan suatu
garis tertentu.
PENGERTIAN

5. Perhatikan gambar
A
B
C
C`
P
F l
g/d
Keterangan
1. Titik A dan B terletak pada
parabola
2. Titik P adalah puncak parabola
3. Titik F adalah titik fokus (titik api)
4. Garis g / d adalah garis arah
(direktris)
5. Garis l merupakan sumbu simetri
6. Garis CC`disebut lactus rektum
(LR)
Jarak dari titik A ke garis g dan titik fokus adalah
sama. Begitu juga halnya dengan titik B.

6.  A. persamaan PARABOLA yang berpuncak di O (0, 0)
(0,0) X
d:X=
-P
F(P,0)
Y
• • •
Terbuka ke kanan
X
Y
• • •
(0,0) F(P,0)
d:X=-P
Terbuka ke kiri
X
Y
F(0,p)
•
•
(0,0)
•
d:y=-P
Terbuka ke atas
X
•
•
(0,0)
•
F(0,-p)
d: y=p
Terbuka ke bawah
GRAFIK

7.  A. persamaan PARABOLA yang berpuncak di O (0, 0)
Puncak Fokus Direktris Persamaan Keterangan
(0, 0) (p, 0) x = -p y2 = 4px Parabola terbuka ke kanan
(0, 0) (-p, 0) x = p y2 = -4px Parabola terbuka ke kiri
(0, 0) (0, p) y = -p x2 = 4py Parabola terbuka ke atas
(0, 0) (0, -p) y = p x2 = -4py Parabola terbuka ke bawah

8. Contoh:
1.Dari parabola-parabola berikut tentukan koordinat
fokus,persamaan sumbu simetri,persamaan direktris dan
panjang lactus rectum
a. y2 = 4x c. x2 = -8y
b. y2 = -12x
Jawab:
a. y2 =4px y2 = 4x, maka p = 1
Parabola ini merupakan parabola horizontal yang
terbuka ke kanan.
(i) Koordinat titik fokus F(p,0) F(1,0)
(ii) Sumbu semetri berimpit dengan sumbu X, maka
persamaanya y = 0
(iii) Persamaan direktris: x = -p x = -1
(iv) Panjang lactus rectum (LR) = 4p = 4 . 1 = 4

9. b. y2 =-p4x y2 = -12x, maka 4p = 12 p = 3
Parabola ini merupakan parabola horizontal yang terbuka
ke kiri
(i) Koordinat titik fokus F(-p,0) F(-3,0)
(ii) Sumbu semetri berimpit dengan sumbu X, maka
persamaanya y = 0
(iii) Persamaan direktris: x = -p x = 3
(iv) Panjang lactus rectum (LR) = 4p = 4 . 3= 12
x = 0
(iii) Persamaan direktris: y = p y = 2
(iv) Panjang lactus rectum (LR) = 4p = 4 . 2 = 8
c. x2 = -8y, maka 4p = 8 p = 2
Parabola ini merupakan parabola horizontal yang
terbuka ke bawah
(i) Koordinat titik fokus F(0,-p) F(0,-2)
(ii) Sumbu semetri berimpit dengan sumbu y, maka
persamaanya x2 = -p4y

10.  B. persamaan PARABOLA yang berpuncak di P (a, b )
•
•
Fp(a+p,b)
• x • Keterangan
a. Titik puncak P(a,b)
b. Titik fokus F(a+p,b)
c. Direktris x = -p+a
d. Sumbu semetri y = b
•
O(0,0) F(p,0)
•
• •
y
P(a,b)
a
•
(y – b)2 = 4p(x – a)

11. GRAFIK
y
O
g
F
x
Terbuka ke kanan
O
g
x
y
F
Terbuka ke kiri
y
F
O
g
x
Terbuka ke atas
y
F
O
x
g
Terbuka ke bawah
 B. persamaan PARABOLA yang berpuncak di P (a, b )

12.  B. persamaan PARABOLA yang berpuncak di P (a, b )
Puncak Fokus Direktris Persamaan Keterangan
(a, b) (a + p, b) x = -p + a (y – b)² = 4p(x – a) Terbuka ke kanan
(a, b) (a - p, b) x = p + a (y – b)² = -4p(x – a) Terbuka ke kiri
(a, b) (a, b + p) y = -p + b (x – a)² = 4p(y – b) Terbuka ke atas
(a, b) (a, b – p) y = p + b (x – a)² = -4p(y – b) Terbuka ke bawah

13. Contoh:
Diberikan persamaan parabola 3x – y2 + 4y + 8= 0
Tentukan : a. Titik puncak c. Direktris
b. Titik fokus d. Sumbu semetri
Jawab:
Ubah persamaan parabola ke persamaan umum:
3x – y2 + 4y + 8= 0
y2 - 4y = 3x + 8
y2 - 4y + 4 = 3x + 8 + 4
(y – 2)2 = 3x + 12
(y – 2)2 = 3(x + 4)
Didapat persamaan parabola (y – 2)2 = 3(x + 4) yaitu
parabola mendatar yang terbuka ke kanan.

14. Dari persamaan tersebut diperoleh:
a. Titik puncak P(-4,2)
b. 4p = 3 maka p =
3
4
Titik Fokus F(a+p,b)
3
,2)
4
F(4 
,2)
1
4
F(3
c. Persamaan direktris :
x p a
     
d. Sumbu semetrinya : y = 2
3
4
4
4
3
4
 
x
O(0,0) x
F
P(-4,2)
y

15.  C. Garis singgung PARABOLA
a. Persamaan Garis Singung melalui satu titik pada PARABOLA
x
y
•
A•(x1,y1)
h
0
 Perhatikan Gambar di samping,
Garis h adalah garis singgung parabola y² = 4px di
titik A(x1,y1).

16. • Secara umum, persamaan garis singgung parabola di
titik A(x1,y1). Di sajikan pada tabel berikut.
y2 = 4px yy1 = 2p(x+x1)
y2 = -4px yy1 = -2p(x+x1)
x2 = 4py xx1 = 2p(y+y1)
x2 = -4py xx1 = -2p(y+y1)
(y – b)2 = 4p(x – a) (y-b)(y1-b)=2p(x+x1-2a)
(y – b)2 = -4p(x – a) (y-b)(y1-b)=-2p(x+x1-2a)
(x – a)2 = 4p(y – b) (x-a)(x1-a)=2p(y+y1-2b)
(x – a)2 = -4p(y – b) (x-a)(x1-a)=-2p(y+y1-2b)

17. Tentukan persamaan garis singgung parabola y2 = 8x di
titik (2,4)
jawab :
y2 = 8x
4p = 8
p = 2
Titik A(x1,y1) A(2,4)
Persamaan garis singgungnya adalah
yy1 = 2p(x+x1)
y.4 = 2.2(x+2)
4y = 4(x+2)
y = x+2
Contoh:

18.  C. Garis singgung PARABOLA
b. Persamaan Garis Singung PARABOLA yang Bergradienm
• Secara umum, persamaan garis singgung parabola dengan gradienm
dapat di lihat pada tabel berikut.
Persamaan parabola Persamaan garis singgung
y2 = 4px y = mx +
p
m
p
y2 =- 4px y = mx -
m
x2 = 4py y = mx – m2p
x2 = -4py y = mx + m2p
p
(y – b)2 = 4p(x – a) (y – b) = m(x – a) +
m
p
(y – b)2 = -4p(x – a) (y – b) = m(x – a) -
m
(x– a)2 = 4p(y – b) (y – b) = m(x – a) – m2p
(x– a)2 = -4p(y – b) (y – b) = m(x – a) + m2p

19. Contoh:
Tentukan persamaan garis singgung parabola y2 = 8x
yang bergradien 2
Jawab:
Parabola y2 = 8x
4p = 8
p = 2
Maka persamaan garis singgungnya adalah:
y = mx +
y = 2x + 1
p
m

20. Sekian dan Terima Kasih