Dokumen ini membahas penerapan integral dalam menyelesaikan persamaan diferensial dan menghitung luas serta volume daerah yang dibatasi oleh kurva. Terdapat contoh-contoh konkret tentang hukum pendinginan Newton, luas daerah yang dibatasi dua kurva, dan volume benda pejal menggunakan metode silinder dan cincin. Selain itu, dokumen juga menyentuh tentang fungsi densitas dalam probabilitas dan memberikan langkah-langkah untuk menghitung area dan volume.

1. MODUL VI :
PENERAPAN INTEGRAL

2. PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah persamaan yang memuat sebuah fungsi yang
tidak diketahui dan turunan-turunannya. Menyelesaikan suatu persamaan
diferensial adalah mencari suatu fungsi yang tidak diketahui.
Contoh
x4cosx2
dx
dy
3yy2
x31
dx
dy
2x4
dx
yd 2
2
2
Persamaan
diferensial orde
satu variabel
terpisah
Persamaan diferensial linier orde dua
PD orde satu variabel terpisah
)y(g
)x(f
dx
dy
atau
f(x)dx + g(y) dy = 0
dx)x(fdy)y(g
cdy)y(gdx)x(f
atau

3. Contoh penerapan
Hukum Pendinginan Newton
Hukum Newton menyatakan bahwa
laju perubahan laju pendinginan
suhu benda sebanding dengan
selisih suhu antara benda dan
medium yang mengelilinginya.
Andaikan t adalah waktu t setelah
benda mulai mendingin. Jika T(t)
adalah suhu benda pada saat t, Tm
suhu medium yang mengelilinginya,
dT/dt laju perubahan suhu pada
saat t, dan k faktor pembanding
maka,
)TT(k
dt
dT
m
Rangkaian Listrik R-L
Pada rangkaian seri menyatakan
bahwa hubungan antara hambatan
R ohm dan induktansi L henry
dengan sebuah sumber arus listrik
konstan yang tegangannya V volt.
Andaikan i(t) menyatakan arus listrik
dalam ampere yang mengalir pada
rangkaian setelah waktu t, dan t
menyatakan waktu dalam detik sejak
rangkaian ditutup. Menurut hukum
Kircoff, diperoleh :
VRi
dt
di
L

4. PENERAPAN INTEGRAL TENTU
Luas Bidang Datar
Misalkan daerah R dibatasi oleh
kurva y=f(x), sumbu x pada [a,b]
seperti pada gambar
R
y=f(x)
f(xi)
xi
x=a x=b
Ai=f(xi) xi, a xi b
Luas empat persegi panjang
b
a
dx)x(f)R(A
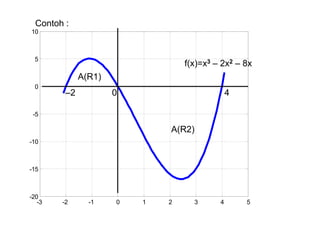
Contoh 1
Hitunglah luas daerah R, yang terletak
dibawah kurva f(x) = 4x2 – x3, sumbu x,
garis x = 1 dan garis x = 3.
Jawab
x=1 x=3
f(xi)
x
y
f(x) = 4x2 – x3
Ai=(4xi2 – xi3) xi, 1 xi 3
3
44
dx)xx4()R(A
3
1
32

5. -3 -2 -1 0 1 2 3 4 5
-20
-15
-10
-5
0
5
10
f(x)=x3 – 2x2 – 8x
Contoh :
A(R1)
A(R2)
–2 0 4

6. Luas diantara dua kurva
Misalkan daerah R dibatasi oleh dua
kurva y=f(x), y=g(x) pada [a,b]
seperti pada gambar
f(x)-g(x)
xi
R
y=f(x)
y=g(x)
x
y
x=a x=b
Luas empat persegi panjang :
Ai=[f(xi) – g(xi)] xi, a xi b
b
a
dx)]x(g)x(f[)R(A
Prosedur Menghitung Luas Daerah
Langkah-langkah untuk menghitung
luas daerah dengan integral tertentu
(1)Buatlah gambar daerah R yang
bersangkutan, beserta batas-
batasnya.
(2)Pada daerah R buatlah suatu jalur
tertentu.
(3)Hampiri luas suatu jalur tertentu
langkah 2 dengan luas empat
persegi panjang.
(4)Jumlahkan luas aproksimasi dari
langkah 3.
(5)Ambil limitnya sehingga diperoleh
suatu integral tertentu.

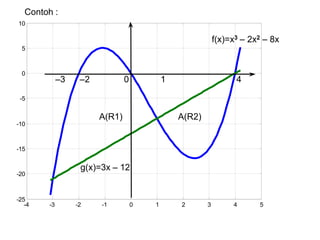
7. Contoh 2
Hitunglah luas daerah R, terletak
y = 4x2 – x3, dan x+y = 4.
Jawab :
Sketsa grafik R lihat gambar berikut
R2
R1
g(x)=4-x
f(x) = 4x2 – x3
x=-1 x=1 x=4
x
y
A2
A1
Titik potong kedua kurva diperoleh :
4-x = 4x2 -x3
X3-4x2 – x + 4 = 0, x1=-1,x2=1,x3=4
Menghitung A(R)
A1 = [g(xi)-f(xi)] xi
= [(4-xi)-(4xi
2 – xi
3)] xi, -1 xi 1
1
1
32
1 dx)]xx4()x4[()R(A
3
16
4
x
3
x4
2
x
x4
1
1
432
A2 = [f(xi)-g(xi)] xi
= [(4xi
2 – xi
3)-(4-xi)] xi, 1 xi 4
4
1
32
2 dx)]x4()xx4[()R(A
4
63
4
x
3
x4
2
x
x4
4
1
432
12
253
4
63
3
16
)R(A

8. -4 -3 -2 -1 0 1 2 3 4 5
-25
-20
-15
-10
-5
0
5
10
f(x)=x3 – 2x2 – 8x
g(x)=3x – 12
–3 –2 0 1 4
A(R1) A(R2)
Contoh :

9. Fungsi Densitas :
Fungsi f(x) dikatakan sebagai fungsi densitas (probabilitas), jika hanya jika
f(x) memenuhi sifat-sifat berikut ini :
(1) f(x) 0
dx)x(f)bxa(P)3(
1dx)x(f)2(
b
a
Mean dan variannya diberikan oleh :
2222
)]x(E[)x(E)x(E
dx)x(xf)x(E

10. Soal 1
Suatu fungsi densitas (kepadatan)
didefinisikan oleh
(i) f(x) = k x (2 – x)4, 0 x 2
(ii) f(x) = kxa(8 – x3) 0 x 2
(III) f(x) = kxb(4 – x2), 0 x 2
(a) Hitunglah nilai k
(b) Berapa, P(x>1)
(c) Hitunglah E(x) dan varian
Soal 2
Hitunglah luas daerah yang
dibatasi oleh kurva, berikut
dengan sumbu x
(a) f(x)=(x+a)(x – 1)(x – a – 1)
(b) f(x) = (x2 – 1 )(x – a – 1)
TUGAS LUAS BIDANG DATAR
Soal 3.
Hitunglah luas daerah yang dibatasi
oleh kurva berikut ini:
(a). y = a – (x – 4)2, dan x + y = (a + 2),
(b). y = x2, x + y = 2, dan x=y3.
(c). y = x2, y = 8 – x2, dan 4x–y+12 = 0.
Soal 4. Hitunglah luas segitiga dimana
titik-titik sudutnya adalah :
(a). (1,2), (7,4), dan (-1,8)
(b). (2,1), (6,5), dan (0,8)
Soal 5. Hitunglah luas segiempat
dimana koordinat titiktitik sudutnya
adalah
(a). (1,1), (4,2), (–2, 6) dan (2,7)
(b). (2,1), (5,3), (–2,7) dan (1,9)

11. Volume Benda Pejal, Metode Silinder
Perhatikanlah sketsa silinder
berikut ini
r
h V= r2h
r1
r2
h
hrrV 2
1
2
2
Andaikan daerah R dibatasi oleh f(x),
sumbu x, garis x = a dan garis x = b.
y=f(x)
y
f(xi)
xi
x=a x=b
x
R
r=f(xi)
h= xi
Jika R diputar terhadap sumbu x
dihasilkan benda pejal. Elemen volume
V = r2h
= [f(xi)]2 xi, a xi b
Jadi : b
a
2dx)]x(f[V

12. Contoh 3 :
Hitung volume benda pejal daerah
R yang dibatasi oleh y=1+(x-1)2,
sumbu x, dari x=1 sd x=3, jika
diputar tehadap sb x
Jawab
h= xi
r=f(xi)
x
y
x=3
x=1
y=1+(x-1)2
V = r2h
= [1+(x-1)2]2 xi, 1 xi 3
15
206
])1(1[3
1
22
dxxV
Hitung volume benda pejal daerah
R yang dibatasi oleh y=1+(x-1)2,
garis y=5, dari x=1 sd x=3, jika
diputar terhadap garis y=5
Jawab
x
y=5
r=5-f(xi)
y=1+(x-1)2
x=1
x=3
R
R
V = r2h = [4-(x-1)2]2 xi, 1 xi 3
15
256
])1(4[3
1
22
dxxV

13. Metode Cincin, Silinder
Misalkan daerah R dibatasi oleh kurva-kurva y = f(x) dan y = g(x), garis x = a
dan garis x = b, dengan f(x) g(x). Andaikan daerah R diputar dengan sumbu
putar sumbu x, maka akan dihasilkan suatu benda pejal, dimana bagian
tengahnya lubang. Metode demikian disebut metode cincin
xi y=f(x)
y=g(x)
x=a x=b
R
f(x)-g(x)
x
y
r1=g(x)
r2=f(x)
y
h= xi
Dengan metode silinder :
V= [r2
2 – r1
2]h
= [f(xi)2–g(xi)2] xi,a xi b
dx])x(g)x(f[V 2
b
a
2

14. Contoh 4
Daerah R dibatasi oleh, y=6-x dan
y=(x-3)2+1. Hitung volume bendanya,
jika R diputar terhadap sumbu x,
garis y=6, y=1
Jawab :
Kasus 1. Sumbu putar sumbu x
y=f(x)=6-x
y=g(x)=(x-3)2+1
r1=g(x)
r2=f(x)
h= xi
x
Karena, A SP . dengan metode
silinder :
V= [r2
2 – r1
2]h
= [f(x)2–g(x)2] x,1 x 4
= [(6-x)2–(1+(x-3)2)2] x,1 x 4
Jadi,
dx}])3x(1[)x6{(V
4
1
222
R
a=1 b=4
4
1
533
4
1
422
5
)3x(
3
)3x(2
x
3
)x6(
dx})3x()3x(21)x6{(
5
117
V

15. Kasus 2 : Sumbu putar garis y = 6
r1=6-f(x)
r2=6-g(x)
y=6
y=f(x)=6-x
y=g(x)=(x-3)2+1
R
a=1 b=4
x
y
h= xi
Karena, A SP, Dengan metode
silinder :
V= [r2
2 – r1
2]h
= {[6-g(x)]2–[6-f(x)]2} x,1 xi 4
= {[6–(1+(x-3)2)]2-[6-(6-x)]2} x,
= {[5–(x-3)2]2- x2} x, 1 x 4
Jadi,
5
153
3
x
5
)3x(
3
)3x(10
x25
dx}x)3x()3x(1025{
dx}x])3x(5{[V
4
1
353
4
1
242
4
1
222

16. Kasus 3 : Sumbu putar garis y = 1
y=1
x
y
y=g(x)=(x-3)2+1
y=f(x)=6-x
r1=g(x)-1
r2=f(x)-1
R
h= xi
a=1 b=4
Karena, A SP, maka dengan metode
silinder :
V= [r2
2 – r1
2]h
= {[f(x)-1]2– [g(x)-1]2} x,1 x 4
= {[(6–x)-1]2 – [(1+(x-3)2)-1]2} x,
= {[5–x]2 – (x-3)4} x, 1 x 4
Jadi,
5
72
5
)3x(
3
)x5(
dx})3x()x5{(V
4
1
53
4
1
42

17. Metode Sel Silinder
Perhatikanlah sel silinder berikut ini
r2
r
r1
r1 : jari-jari dalam
r2 : jari-jari luar
r : jari-jari rata-rata
h : tinggi silinder
h h)rr(
2
rr
2 12
12
Volume sel silinder adalah :
V = r2
2h – r1
2 h
= [r2
2 – r1
2 ] h
= (r2 + r1)(r2 – r1)h
Jika diambil
2
rr
r 12
r = r2 – r1
Dihasilkan rumus
V = 2 r h r

18. Volume benda pejal, Metode Sel
Silinder
Andaikan daerah R dibatasi oleh f(x),
sumbu x, garis x = a dan garis x = b.
x=bx=a
R y=f(x)
r= xi
r=x
h=f(x)
Jika R diputar terhadap sumbu y
dihasilkan benda pejal. Elemen volume
V = 2 rh r
= 2 x f(x) x, a x b
Jadi : b
a
dx)x(xf2V
Contoh 5 :
Hitung volume benda pejal jika R
dibatasi oleh y=1+(x-1)2, sumbu x,
dari x=1 sd x=3, diputar terhadap y
Jawab
r=x
h=f(x)
r= xi
R
x=1 x=3
V = 2 rh r = 2 x f(x) x
=2 x[1+(x-1)2] x, 1 x 3
Jadi,
3
64
dx))1x(1(x2V
3
1
2

19. Metode Sel Silinder Lanjutan
Misalkan daerah R dibatasi oleh kurva-kurva y = f(x) dan y = g(x), garis x = a
dan garis x = b, dengan f(x) g(x). Andaikan daerah R diputar dengan sumbu
putar sumbu y, maka akan dihasilkan suatu benda pejal, berbentuk sel
silinder. Metode demikian disebut metode sel silinder
xi y=f(x)
y=g(x)
x=a x=b
R
h=f(x)-g(x)
x
y
h=f(x)-g(x)r=x
y
r= x
Dengan metode sel silinder :
V= 2 r h r
= 2 x[f(x)–g(x)] x, a x b
dx)]x(g)x(f[x2V
b
a
x

20. Contoh 4
Daerah R dibatasi oleh, y=6-x dan
y=(x-3)2+1. Hitung volume bendanya,
jika R diputar terhadap sumbu y,
garis x=1, dan x=4
Jawab :
Kasus 1. Sumbu putar sumbu y
Karena A // SP, maka dengan metode
sel silinder :
V= 2 r h r
= 2 x [f(x)–g(x)] x,1 x 4
= 2 x [(6-x)–(1+(x-3)2)] x,1 x 4
Jadi,
dx})3x()x5{(x2V
4
1
2
4
1
4332
4
1
322
4
)3x(
3
)3x(3
3
x
2
x5
2
dx})3x()3x(3xx5{2
2
45
V
r=x
y=6-x
y=(x-3)2+1
R
x=1 x=4
x
y
h=f(x)-g(x)
r= xi

21. Kasus 2 : Sumbu putar garis x=1
y=6-x
1
x
r=x-1
h=f(x)-g(x)
y=(x-3)2+1
r= xi
Dengan metode sel silinder
V = 2 r h r
= 2 (x-1)[(6-x) – (1+(x-3)2] x,
Jadi,
)2/27(
dx})3x(x5){1x(2V
4
1
2
x=1 x=4
Kasus 3 : Sumbu putar garis x=4
h=f(x)-g(x)
r=4-xx
R
r= xi
y=6-x
y=(x-3)2+1
x=1 x=4
Dengan metode sel silinder
V = 2 r h r
= 2 (4 - x)[(6-x) – (1+(x-3)2] x
Jadi,
)2/27(
dx})3x(x5){x4(2V
4
1
2

22. Prosedur Menghitung Volume Benda Pejal
Langkah-langkah untuk menghitung volume benda pejal dengan integral
tertentu adalah sebagai berikut :
(1)Buatlah gambar daerah R yang bersangkutan, tentukan fungsi f(x)
dan g(x) beserta batas-batasnya (batas integral).
(2)Pada daerah R buatlah suatu jalur tertentu (luas empat persegi
panjang), dan buatlah sumbu putarnya yang tidak memotong daerah
R.
(3)Hampiri volume benda pejalnya dengan pendekatan :
(a) Volume silinder, V = r2h jika A tegak lurus dengan sumbu putar
(b) Volume sel slilinder, V = 2 rh r, jika A sejajar dengan sumbu
putar.
(4)Jumlahkan volume silinder aproksimasi dari langkah 3.
(5)Ambil limitnya sehingga diperoleh suatu integral tertentu, atau
hitunglah volume benda pejalnya dengan integral tentu.

23. Momen dan Pusat Massa
Misalkan sepotong lamina homogen dibatasi oleh kurva y = f(x) dan y = g(x)
dengan f(x) g(x) garis x = a, dan garis x = b. Andaikan bahwa kerapatan
lamina adalah ,
y=f(x)
y=g(x)
x=a x=b
R
y
x
2
)xi(g)xi(f
xi
xi
Andaikanlah, )y,x( pusat masaa lamina
m
M
ydan,
m
M
x xy
dimana,
My : moment terhadap sumbu y
Mx : moment terhadap sumbu x
m : massa lamina
b
a
dx)]x(g)x(f[m
b
a
22
x
b
ay
dx])x(g)x(f[
2
M
dx)]x(g)x(f[xM

24. Contoh 5
Hitung pusat massa daerah R
dibatasi oleh, y=6-x dan y=(x-3)2+1.
Jika kerapatannya adalah konstan k
Jawab :
y=f(x)
y=g(x)
y=6-x
xi
y=(x-3)2+1
xi
x=1 x=4
k
2
9
3
)3x(
2
)x5(
k
dx)])3x(1()x6[(km
4
1
32
4
1
2
k
4
45
dx)])3x(1()x6[(xkM
4
1
2
y
k
dxxx
k
Mx
10
117
]))3(1()6[(
2
4
1
222
Jadi,
2
5
k)2/9(
k)4/45(
m
M
x
y
5
13
)2/9(
)10/117(
k
k
m
M
y x

25. Teorema Pappus
Jika sebuah daerah R yang terletak pada sebuah bidang diputar
terhadap sebuah garis pada bidang tersebut yang tidak memotong
daerah R, maka volume benda putar yang dibentuk oleh R sama
dengan luas daerah R dikalikan dengan keliling yang ditempuh oleh
titik pusat R itu
Bilamana daerah diputar terhadap sebuah sumbu putar yang tidak
terletak pada daerah R, maka volume benda putarnya diberikan oleh,
V = 2 r A
dimana r adalah jari-jari lingkaran yakni panjang jarak tegak lurus dari
titik pusat massa ke sumbu putar, dan A adalah luas daerah R, lamina.

26. Tugas Khusus Volume Benda Putar
Soal 1. Perhatikanlah daerah R dibatasi oleh, y = (b – 5) + (x – a + 4)2
dan garis lurus yang menghubungkan titik (a–5, b–4) dan (a–2,b –1).
Hitunglah volume benda putarnya, jika daerah R diputar terhadap :
(a). Garis y = b – 6, y=b+5
(b). Garis x = a +1 , x=a – 6
Soal 2. Suatu daerah R dibatasi oleh kurva, y = a – (x – b)2, dan x + y =
(a + b – 2), hitunglah volume benda putarnya, jika daerah R diputar
terhadap :
a. garis y = a+1, y=a - 5
b. garis x = b + 3, x=b – 3
Soal 3. Daerah R adalah sebuah segitiga dimana titik-titik ujungnya
adalah (a,b), (2a,2b), dan (a,2a+2b). Dengan integral tentu hitunglah,
a. Volume benda putarnya jika R diputar terhadap garis y = b
b. Volume benda putarnya jika R diputar terdadap garis x = a

27. Soal 5.
Tugas Massa dan Pusat Massa
a. Untuk soal nomor 1,2 dan 4
hitunglah pusat massa dengan
asumsi kerapatan konstan
b. Hitunglah volume yang
ditanyakan dengan metode
teorema pappus.
Soal 4
Perhatikanlah gambar daerah berikut ini
Hitunglah volume benda putarnya jika
daerah R diputar terhadap :
(a). Garis, y=b-5,
(b). Garis, y= b+1
(c). Garis, x=a – 3
(d). Garis, x = a + 2
Gambar Soal No. 4