For More Information : eac.ryeosomnia@gmail.com

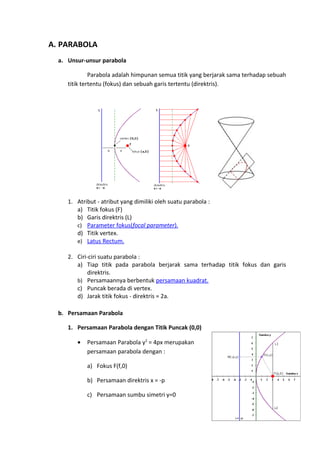
1. A. PARABOLA
a. Unsur-unsur parabola
Parabola adalah himpunan semua titik yang berjarak sama terhadap sebuah
titik tertentu (fokus) dan sebuah garis tertentu (direktris).
1. Atribut - atribut yang dimiliki oleh suatu parabola :
a) Titik fokus (F)
b) Garis direktris (L)
c) Parameter fokus(focal parameter).
d) Titik vertex.
e) Latus Rectum.
2. Ciri-ciri suatu parabola :
a) Tiap titik pada parabola berjarak sama terhadap titik fokus dan garis
direktris.
b) Persamaannya berbentuk persamaan kuadrat.
c) Puncak berada di vertex.
d) Jarak titik fokus - direktris = 2a.
b. Persamaan Parabola
1. Persamaan Parabola dengan Titik Puncak (0,0)
• Persamaan Parabola y2
= 4px merupakan
persamaan parabola dengan :
a) Fokus F(f,0)
b) Persamaan direktris x = -p
c) Persamaan sumbu simetri y=0

2. • Persamaan Parabola x2
= 4py merupakan persamaan parabola dengan :
a) Fokus (0,p)
b) Persamaan direktris y = -p
c) Persamaan sumbu simetri x = 0
2. Persamaan Parabola dengan Titik Puncak (a,b)
• Persamaan Parabola (y-b)2
= 4p(x-a) merupakan persamaan parabola
dengan :
a) Fokus F(p+a,b)
b) Persamaan direktris x=-p+b
c) Perrsaman sumbu simetri x = a
c. Persamaan Garis Singgung Parabola
1. Persamaan Garis Singgung Parabola dengan Gradien m
Syarat garis menyinggung parabola adalah D = 0 sehingga n = -m2
p.
Persamaan garis singgung dengan gradien m pada parabola :
a) y2
= 4px adalah y = mx +
b) x2 = 4py adalah y = mx – m2
p
c) (y-b)2
= 4p(x-a) adalah y-b = m(x-a) +
d) (x-a)2
= 4p(y-b) adalah y-b = m(x-a) + m2
p
2. Persamaan Garis Singgung Parabola di Titik P(x1,y1)
Titik P(x1,y1) terletak pada kurva parabola y2
=4px sehingga didapat
persamaan garis singgung sebagai berikut :
a) y2
= 4px adalah y1y = 2p(x+x1)
b) x2
= 4py adalah x1x = 2p(y+y1)

3. c) (y-b)2
= 4p(x-a) adalah (y1-b)(y-b) = 2p(x+x1)
d) (x-a)2
= 4p(y-b) adalah (x1-a)(x-a) = 2p(y+y1)
B. ELIPS
a. Unsur-unsur Elips
Elips adalah tempat kedudukan titik-titik yang memiliki hasil penjumlahan
jarak terhadap dua titik tertentu tetap nilainya, kedua titik tertentu disebut fokus
(F). Sebuah elips adalah gambar yang menyerupai lingkaran yang telah
dipanjangkan ke satu arah.
b. Persamaan Elips
1. Persamaan Elips dengan Titik Pusat (0,0)
• Persamaan elips (berfokus pada sumbu x)
merupakan persamaan elips dengan :
a) Pusat (0,0)
ELIPS

4. b) Fokus F1 (c,0) dan F2 (-c,0) dengan
c) Puncak A1 (a,0), A2 (-a,0), B1 (0,b), B2 (0,-b)
d) Sumbu utama y=0 , sumbu sekawan x= 0
e) Panjang sumbu mayor = 2a, panjang sumbu minor = 2b
Keterangan
 Titik pusat : Titik yang merupakan perpotongan dua sumbu pada elips.
 Fokus : Koordinat titik yang terletak pada sumbu terpanjang elips
yang
jaraknya sama dengan titik pusat.
 Sumbu mayor : Sumbu yang dibentuk oleh dua titik yang jaraknya paling
jauh
pada elips.
 Sumbu minor : Sumbu yang dibentuk oleh dua titik yang jaraknya paling
dekat
pada elips.
• Persamaan elips (berfokus pada sumbu y) merupakan
persamaan elips dengan :
a) Pusat (0,0)
b) Fokus F1 (0,c) dan F2 (0,-c)
c) Puncak A1 (0,a), A2 (0,-a), B1 (b,0), B2 (-b,0)
d) Sumbu utama x = 0 , sumbu sekawan y = 0
e) Panjang sumbu mayor= 2a, panjang sumbu minor = 2b
2. Persamaan Elips dengan Titik Pusat (p,q)
• Persamaan elips (sejajar sumbu x) merupakan
persamaan elips dengan :

5. a) Pusat (p,q)
b) Fokus F1 (p+c, q) dan F2 (p-c, q)
c) Puncak A1 (p+a, q), A2 (p-a, q), B1 (p, q+b), B2 (p, q-b)
d) Sumbu utama y = q , sumbu sekawan x = p
e) Panjang sumbu mayor = 2a, panjang sumbu minor = 2b
• Persamaan elips (sejajar sumbu y) merupakan
persamaan elips dengan :
a) Pusat (p,q)
b) Fokus F1 (p, q+c) dan F2 (p, q-c)
c) Puncak A1 (p, q+a), A2 (p, q-a), B1 (p+b, q), B2 (p-b, q)
d) Sumbu utama x = p , sumbu sekawan y = q
e) Panjang sumbu mayor = 2a, panjang sumbu minor = 2b
c. Persamaan Garis Singgung Elips
1. Persamaan Garis Singgung Elips dengan Gradien m

6. Sebuah garis g: y = mx+n bersinggungan dengan kurva elips
Lalu mensubstitusikan y = mx+n ke dalam
diperoleh :
Bentuk tersebut merupakan persamaan kuadrat dalam x. Syarat garis
menyinggung parabola adalah D=0 sehingga diperoleh
Dengan proses yang sama, dapat juga mensubstitusikan y = mx + n ke dalam
persamaan elips lainnya. Sehingga didapatkan hasil :
a)
adalah
b)
adalah
c)
adalah
d)
adalah
2. Persamaan Garis Singgung Elips di Titik P (x1, y1)

7. Titik P (x1, y1) terletak pada kurva elips dengan begitu
dapat ditentukan persamaan garis singgung di titik tersebut. Persamaan garis
singgung di titik P (x1, y1) pada elips :
a)
adalah
b) adalah
c)
adalah
d)
adalah
C. HIPERBOLA
a. Unsur-unsur Hiperbola
Sebuah bidang “P” memotong / mengiris kerucut. Misal sudut antara garis
pelukis dan tinggi kerucut sebagai α, sudut antara bidang P dan garis tinggi
kerucut sebagai β . Arah peperpotongan bidang P membentuk sudut 0o
< β < α
. Irisan tersebut dinamakan hiperbola seperti pada gambar.

8. Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya terhadap dua
titik tertentu adalah tetap.
• Titik-titik tertentu itu disebut fokus (F1 dan F2)
• Garis yang melalui titik-titik F1 dan F2 disebut sumbu transvers (sumbu utama)/
sumbu nyata
• Titik tengah F1 dan F2 disebut pusat hiperbola (P)
• Garis yang melalui P dan tegak lurus sumbu transvers disebut sumbu konjugasi
(sumbu sekawan)/ sumbu imajiner
• Titik-titik potong hiperbola dan sumbu transvers disebut puncak hiperbola
• Contoh Hiperbola yang mempunyai persamaan paling sederhana :
P

9. b. Persamaan Hiperbola
• Persamaan Hiperbola dengan Titik Pusat (0,0) dan Titik Pusat (p,q)
Irisan
Kerucut
Persamaan Umum
(Dengan : c2
= a2
+ b2
)
Properti
Hiperbola
Horizontal
 Pusat ( 0,0 )
 Fokus (±c,0)
 Puncak (±a,0)
 Asimtot (y)= ±
 Pusat ( p,q )
 Fokus (p±c,q)
 Puncak (p±a,q)
 Asimtot (y - q) = ±
Hiperbola
Vertikal
 Pusat ( 0,0 )
 Fokus (0, ±c)
 Puncak (0, ±a)
 Asimtot (y)= ±
 Pusat ( p,q )
 Fokus (p,q±c)
 Puncak (p,q±a)
 Asimtot (y - q) = ±
• Persamaan Hiperbola yang Berpusat di ( 0,0 )

10. 1) Untuk hiperbola yang berfokus pada sumbu x, persamaan hiperbolanya
adalah :
Irisan
Kerucut
Persamaan Umum
(Dengan : c2
= a2
+ b2
)
Properti
Hiperbola
Horizontal
 Pusat ( 0,0 )
 Fokus (±c,0)
 Puncak (±a,0)
 Asimtot (y)= ±
2) Untuk hiperbola yang berfokus pada sumbu y, persamaan hiperbolanya
adalah :
Irisan
Kerucut
Persamaan Umum
(Dengan : c2
= a2
+ b2
)
Properti
Hiperbola
Vertikal
 Pusat ( 0,0 )
 Fokus (0, ±c)
 Puncak (0, ±a)
 Asimtot (y)= ±

11. • Persamaan Hiperbola yang Berpusat di Titik (p, q)
Irisan
Kerucut
Persamaan Umum
(Dengan : c2
= a2
+ b2
)
Properti
Hiperbola
Horizontal
 Pusat ( p,q )
 Fokus (p±c,q)
 Puncak (p±a,q)
 Asimtot (y - q) = ±
Hiperbola
Vertikal
 Pusat ( p,q )
 Fokus (p,q±c)
 Puncak (p,q±a)
 Asimtot (y - q) = ±

12. c. Persamaan Garis Singgung Hiperbola
• Persamaan Garis Singgung Hiperbola dengan Gradien m
1)
2)
3)
4)
• Persamaan Garis Singgung Hiperbola dengan titik P(x1 , y1)
1)
2)
3)
4)