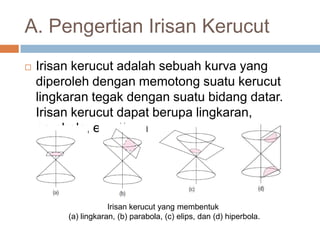
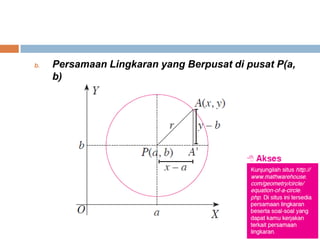
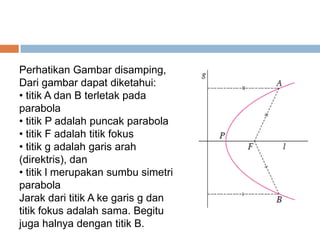
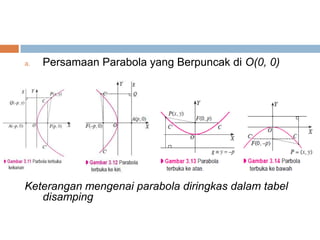
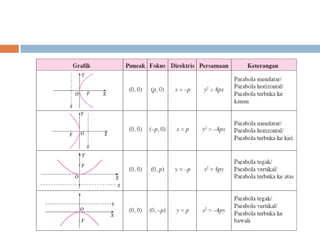
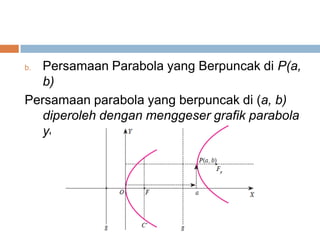
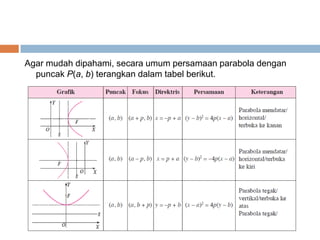
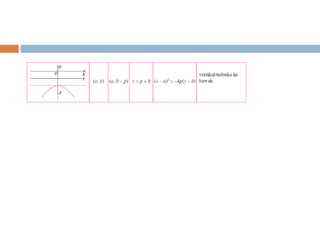
Dokumen ini membahas konsep irisan kerucut yang mencakup lingkaran, parabola, elips, dan hiperbola. Masing-masing jenis irisan kerucut dijelaskan melalui pengertian dan contoh persamaan matematis yang terkait. Terdapat penjelasan lebih lanjut mengenai garis singgung untuk setiap jenis irisan kerucut.

1. BAB 2
IRISAN KERUCUT
Penerbit Erlangga

2. KompetensiDasar
 Menerapkan konsep lingkaran.
 Menerapkan konsep parabola.
 Menerapkan konsep elips.
 Menerapkan konsep hiperbola.

3. A. Pengertian Irisan Kerucut
 Irisan kerucut adalah sebuah kurva yang
diperoleh dengan memotong suatu kerucut
lingkaran tegak dengan suatu bidang datar.
Irisan kerucut dapat berupa lingkaran,
parabola, elips, dan hiperbola.
Irisan kerucut yang membentuk
(a) lingkaran, (b) parabola, (c) elips, dan (d) hiperbola.

4. B. LINGKARAN
 Lingkaran adalah tempat kedudukan titik-titik
yang berjarak sama terhadap sebuah titik
tertentu yang digambarkan pada bidang
Cartesius.
 Jarak yang sama disebut jari-jari lingkaran
 dan titik tertentu disebut pusat lingkaran.

5. 1. Persamaan Lingkaran
a. Persamaan Lingkaran yang Berpusat di O(0,
0)

6. Gambar 3.2 diatas memperlihatkan lingkaran yang
berpusat di O(0, 0) dan jari-jari r pada sebuah
bidang Cartesius.
Misalkan titik A(x, y) adalah sembarang titik yang
terletak pada lingkaran. Titik A′(x, 0) adalah
proyeksi titik A pada sumbu X sehingga ΔOA′A
merupakan segitiga dengan siku-siku di A′.
Dengan menerapkan teorema Pythagoras pada
ΔOA′A, diperoleh:
sadfa
dsfa

7. Karena A(x, y) sembarang titik pada lingkaran,
maka persamaan x2 + y2 = r2 berlaku untuk
semua titik A(x, y) yang terletak pada
lingkaran. Dengan demikian persamaan
lingkaran dengan pusat O(0, 0) dan jari-jari r
adalah:

8. Contoh

9. b. Persamaan Lingkaran yang Berpusat di pusat P(a,
b)

10. Gambar diatas adalah lingkaran yang berpusat
di P(a, b) dan berjari-jari r. Misalkan A(x, y)
adalah sembarang titik yang terletak pada
lingkaran dan AP adalah jari-jari lingkaran.
 Dengan menerapkan Teorema Pythagoras
diperoleh hubungan:

11. Karena titik A(x, y) sembarang, maka
persamaan (x – a)2 + (y – b)2 = r2 berlaku
untuk semua titik A(x, y) yang terletak pada
lingkaran. Dengan demikian persamaan
lingkaran dengan pusat P(a, b) dan jari-jari r
adalah:

12. Contoh

13. c. Bentuk Umum Persamaan Lingkaran

14. C. Parabola
 Parabola adalah tempat kedudukan titik-titik pada
bidang datar yang mempunyai jarak yang sama
terhadap suatu titik tertentu dan suatu garis
tertentu.
 Titik tersebut disebut titik api atau (fokus) dan
garis tersebut disebut garis arah atau (direktris).
 Garis yang melalui titik fokus dan tegak lurus
direktris disebut sumbu simetri.
 Sedangkan segmen garis yang dibatasi oleh
parabola, tegak lurus sumbu simetri, dan melalui
fokus disebut lactus rectum.

15. Perhatikan Gambar disamping,
Dari gambar dapat diketahui:
• titik A dan B terletak pada
parabola
• titik P adalah puncak parabola
• titik F adalah titik fokus
• titik g adalah garis arah
(direktris), dan
• titik l merupakan sumbu simetri
parabola
Jarak dari titik A ke garis g dan
titik fokus adalah sama. Begitu
juga halnya dengan titik B.

16. a. Persamaan Parabola yang Berpuncak di O(0, 0)
Keterangan mengenai parabola diringkas dalam tabel
disamping

18.  Contoh
Tentukan persamaan parabola yang titik fokusnya (4, 0) dan persamaan
direktrisnya x = –4. Tentukan pula panjang lactus rectumnya.
Jawab:
 Buat sketsa parabola dengan diketahui: p = 4
parabola terbuka ke kanan.
 Dari sketsa terlihat bahwa parabolanya
merupakan parabola horizontal yang terbuka
ke kanan, persamaannya adalah: y2 = 4px.
Karena p = 4 maka persamaannya menjadi
y2 = 16x.
 Panjang lactus rectum (LR) = 4p = 4 · 4 = 16.

19. b. Persamaan Parabola yang Berpuncak di P(a,
b)
Persamaan parabola yang berpuncak di (a, b)
diperoleh dengan menggeser grafik parabola
yang berpuncak di (0, 0).

20.  Hasil dari pergeseran tersebut, didapat:
• Titik puncak O(0, 0) menjadi P(a, b)
• Titik fokus F(p, 0) menjadi Fp(a + p, b)
• Direktris x = –p menjadi x = –p + a
• Sumbu simetri y = 0 menjadi y = b
• Persamaan y2 = 4px menjadi (y – b)2 = 4p(x –
a)

21. Agar mudah dipahami, secara umum persamaan parabola dengan
puncak P(a, b) terangkan dalam tabel berikut.

23.  Contoh
Tentukan persamaan parabola yang berpuncak di (2, 4) dan fokus (–3, 4).
Jawab:
Diketahui P(2, 4) dan titik fokus F(–3, 4).
Dengan cara membuat sketsa grafik parabola, maka jenis parabolanya adalah parabola
mendatar yang terbuka ke kiri.
Diketahui: P(a, b) = P(2, 4) dan F(a – p, b) = F(–3, 4).
maka diperoleh: a = 2, b = 4, dan a – p = –3
a – p = –3
⇔ 2 – p = –3
⇔p=5
Sehingga persamaannya adalah:
(y – b)2 = –4p(x – a)
⇔ (y – 4)2 = –4 · 5(x – 2)
⇔ y2 – 8y + 16 = –20(x – 2)
⇔ y2 – 8y + 16 = –20x + 40
⇔ y2 + 20x – 8y – 24 = 0

24. c. Persamaan Garis Singgung Melalui Satu Titik
pada Parabola

25. Contoh

26. d. Persamaan Garis Singgung Parabola yang
Bergradien m

27. 1. Tentukan persamaan garis singgung parabola y2
= 8x yang bergradien 2.
Jawab:
Parabola y2 = 8x 2
y = 4px
⇔ 4p = 8
⇔p=2
Maka persamaan garis singgungnya adalah:
y = mx + m= 2 dan p = 2
⇔ y = 2x + 1

28. D. Elips
 Elips adalah tempat kedudukan titik-titik pada
bidang datar yang jumlah jaraknya terhadap
dua titik tertentu yang diketahui adalah tetap
(konstan).
 Dua titik tertentu itu disebut fokus atau titik api
(F1 dan F2), jarak F1 dan F2 adalah 2c, dan
jumlah jarak tetap adalah 2a (a > 0).

29.  Unsur-unsur pada elips:
i. F1 dan F2 disebut fokus. Jika T adalah sembarang titik
pada elips maka TF1 + TF2 = 2a. F1F2 = 2c, dengan 2a >
2c.
ii. A1A2 merupakan sumbu panjang (sumbu mayor) yang
panjangnya sama dengan jarak tetap yaitu 2a. B1B2
merupakan sumbu pendek (sumbu minor) yang
panjangnya sama dengan 2b. Karena itu a > b.
iii. Lactus rectum yaitu segmen garis yang dibatasi elips,
tegak lurus sumbu mayor, dan melalui fokus (DE dan KL)
panjang lactus rectum
iv. Titik pusat (P) yaitu titik potong sumbu mayor dengan
sumbu minor.
v. Titik puncak elips yaitu titik A1, A2, B1, dan B2

30. 1. Persamaan Elips yang Berpusat di O(0, 0)

31. 2. Persamaan Elips yang Berpusat di Titik P(m,
n)

32. 3. Bentuk Umum Persamaan Elips
Persamaan elips memiliki bentuk umum:

33. 4. Persamaan Garis Singgung Elips
i. Persamaan Garis Singgung Melalui Titik (x1, y1)
pada Elips

34. ii. Persamaan Garis Singgung dengan gradien p

36. D. Hiperbola
 Hiperbola adalah tempat kedudukan titik-titik pada
bidang datar yang selisih jaraknya terhadap dua titik
tertentu adalah tetap.
 Kedua titik tertentu disebut fokus (titik api).
 Jika titik fokus hiperbola adalah F1 dan F2 dan titik pada
hiperbola adalah T, maka |F1T – F2T | = 2a dengan a >
0 dan 2a < F1F2.

37. 1. Persamaan Hiperbola dengan Pusat O(0, 0)

38.  Contoh

40. 2. Persamaan Hiperbola dengan Pusat P(m, n)

41. 3. Persamaan Garis Singgung Hiperbola
i. Persamaan Garis Singgung Melalui Titik (x1, y1) pada
Hiperbola
Persaman garis singgung hiperbol a , di titik T(x1, y1)
yaitu:

42. ii. Persamaan Garis Singgung Hiperbola dengan gradien p