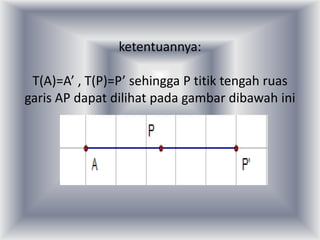
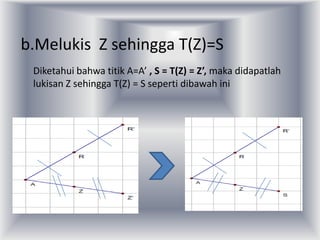
Dokumen ini membahas transformasi pada tiga titik yang tidak segaris dan menyajikan bukti bahwa fungsi padanan t adalah bijektif, sehingga memenuhi syarat untuk menjadi transformasi. Melalui gambar dan penjelasan, dibuktikan bahwa t adalah fungsi surjektif dan injektif. Kesimpulannya, t dapat dianggap sebagai suatu transformasi.

2. Soal nomor 3:
Diketahui tiga titik a, r, s yang berlainan dan
tidak segaris. Ada padanan t yang didefinisikan
sebagai berikut:
T(A)=A, T(P)=P’ sehingga P titik tengah ‘
a) Lukislah R’=T(R)
b) Lukislah Z sehingga T(Z)=S
c) Apakah T suatu transformasi?

3. ketentuannya:
T(A)=A’ , T(P)=P’ sehingga P titik tengah ruas
garis AP dapat dilihat pada gambar dibawah ini

4. Jawab:
a. Melukis R’=T(R)
Dilukis titik-titik A,R,S,Z pada GSP dengan print screen
yang titik-titiknya tidak segaris seperti didalam soal.

5. Kemudian kita dapat :
Melukis R’=T(R)
Dan didapatkan bahwa panjang garis AR sama dengan panjang garis RR’
Karena R’=T(R) maka didapatlah lukisannya sebagai berikut:

6. b.Melukis Z sehingga T(Z)=S
Diketahui bahwa titik A=A’ , S = T(Z) = Z’, maka didapatlah
lukisan Z sehingga T(Z) = S seperti dibawah ini

7. c. Apakah T suatu transformasi?
Seperti yang diketahui bahwa suatu T
dikatakantransformasi apabila T adalah suatu
fungsi bijektif (surjektif dan injektif) dengan
daerah asalnya V (euclide) dan daerah nilainya
V (euclidez) juga.
maka kita buktikan apakah T suatu fungsi
surjektif dan fungsi injektif

8. FUNGSI SURJEKTIF
Menurut ketentuan pertama bahwa A=A prapertanya adalah A
sendiri, sebab T(A)=A
Apabila P ≠A, maka karena V ialah bidang euclide, ada P’ tunggal
dengan P’ sehingga =
Jadi , P adalah titik tengah yang merupakan satu-satunya titik
tengah. Jadi, P=T(P’)
Ini berarti bahwa P’ adalah praperta dari titik P. Dengan demikian
dapat dikatakan bahwa setiap titik euclide(V) memiliki praperta.
Jadi T adalah suatu padanan yang surjektif

9. FUNGSI INJEKTIF
Ambil dua buah titik R≠A, S≠A, dan R ≠S. A,R,S
tidak segaris (koliner), kita akan menyelidiki
kedudukan T(R) dan T(S).

10. Andaikan T(R) = T(S).
Oleh karena T(R) dan T(S) ε maka dalam hal ini dan
memiliki 2 titik sekutu yaitu A dan T(R) = T(S)
Ini berarti bahwa garis dan berimpit sehingga
mengakibatkan S ini berlawanan dengan permisalan
bahwa, A,R,S tidak segaris
Dan didapatkan bahwa T(R) ≠ T(S) dan itu merupakan
fungsi injektif.
Maka dari uraian tersebut disimpulkan bahwa padanan T
itu injektif dan surjektif , sehingga T adalah padanan yang
bijektif .
Terbukti bahwa T adalah suatu transformasi