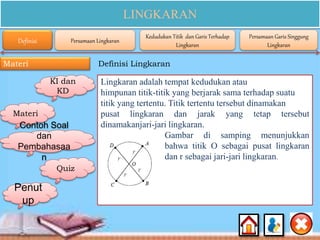
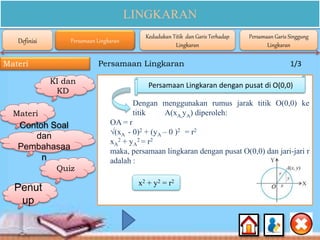
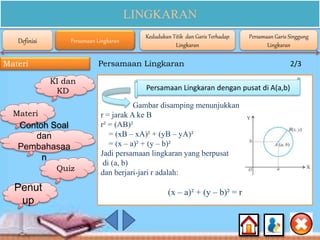
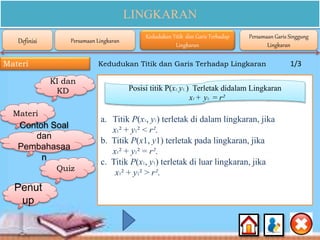
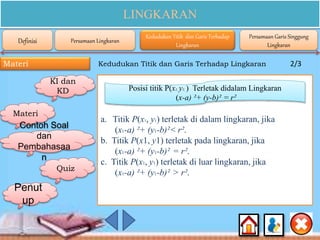
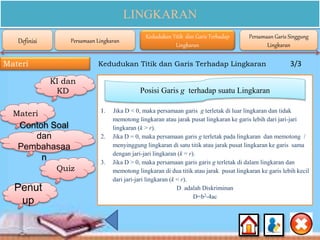
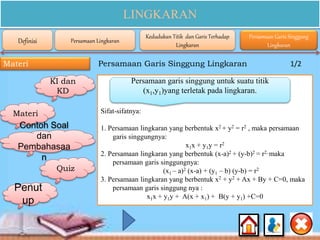
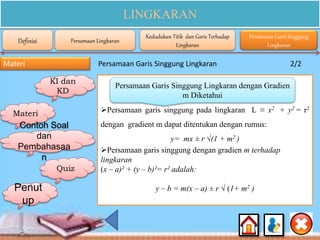
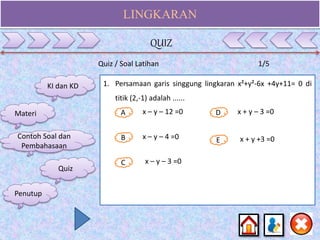
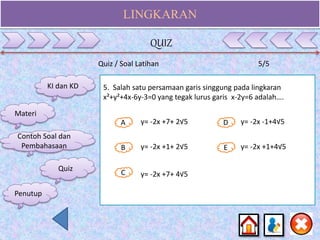
Dokumen ini membahas materi lingkaran untuk siswa SMA kelas XI, mencakup kompetensi inti dan dasar, serta indikator pencapaian yang berkaitan dengan konsep, persamaan, dan sifat-sifat lingkaran. Selain itu, terdapat contoh soal dan penjelasan rinci tentang cara menentukan persamaan lingkaran, posisi titik terhadap lingkaran, dan garis singgung lingkaran. Konten ini dirancang untuk membantu siswa memahami dan menerapkan konsep matematika mengenai lingkaran secara efektif.