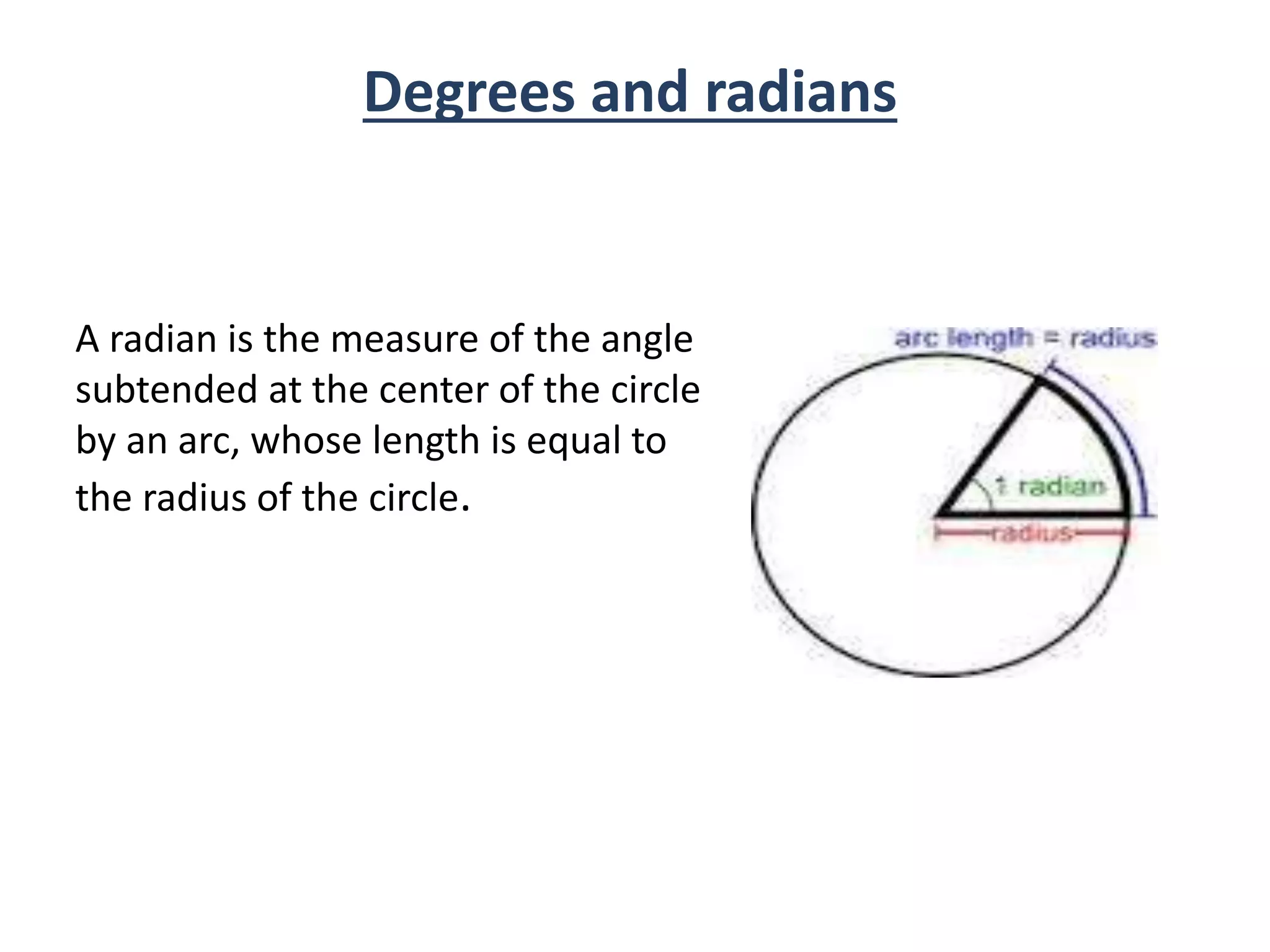
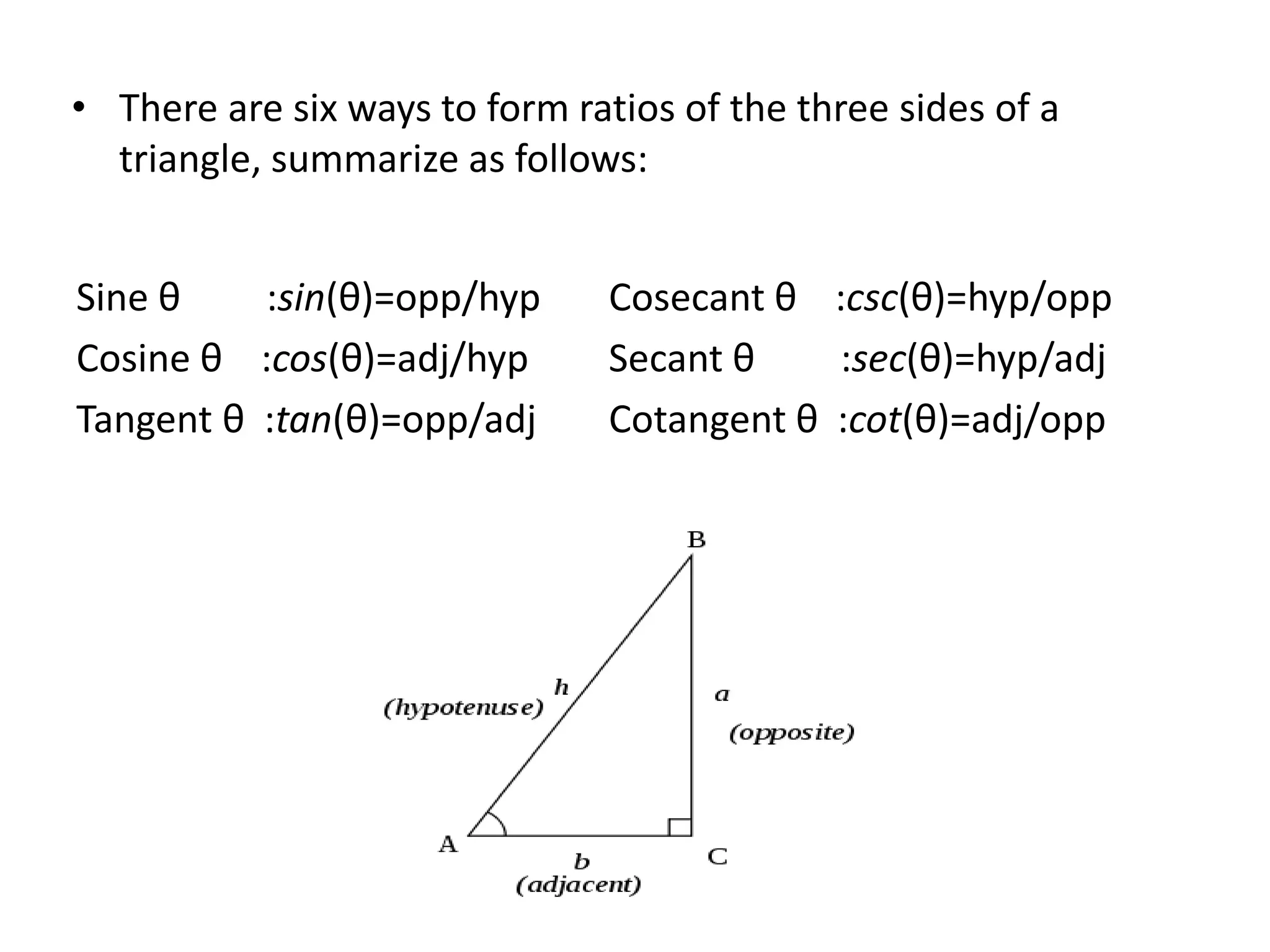
This document introduces trigonometry, including: - Trigonometry is the measurement of triangles and the relationship between sides and angles, derived from Greek words meaning "three", "angles", and "measurement". - Angles are formed by two rays with a common starting point and can be positive or negative depending on direction of rotation. - Trigonometric functions relate ratios of sides of a right triangle to an angle and include sine, cosine, tangent, cotangent, secant, and cosecant. 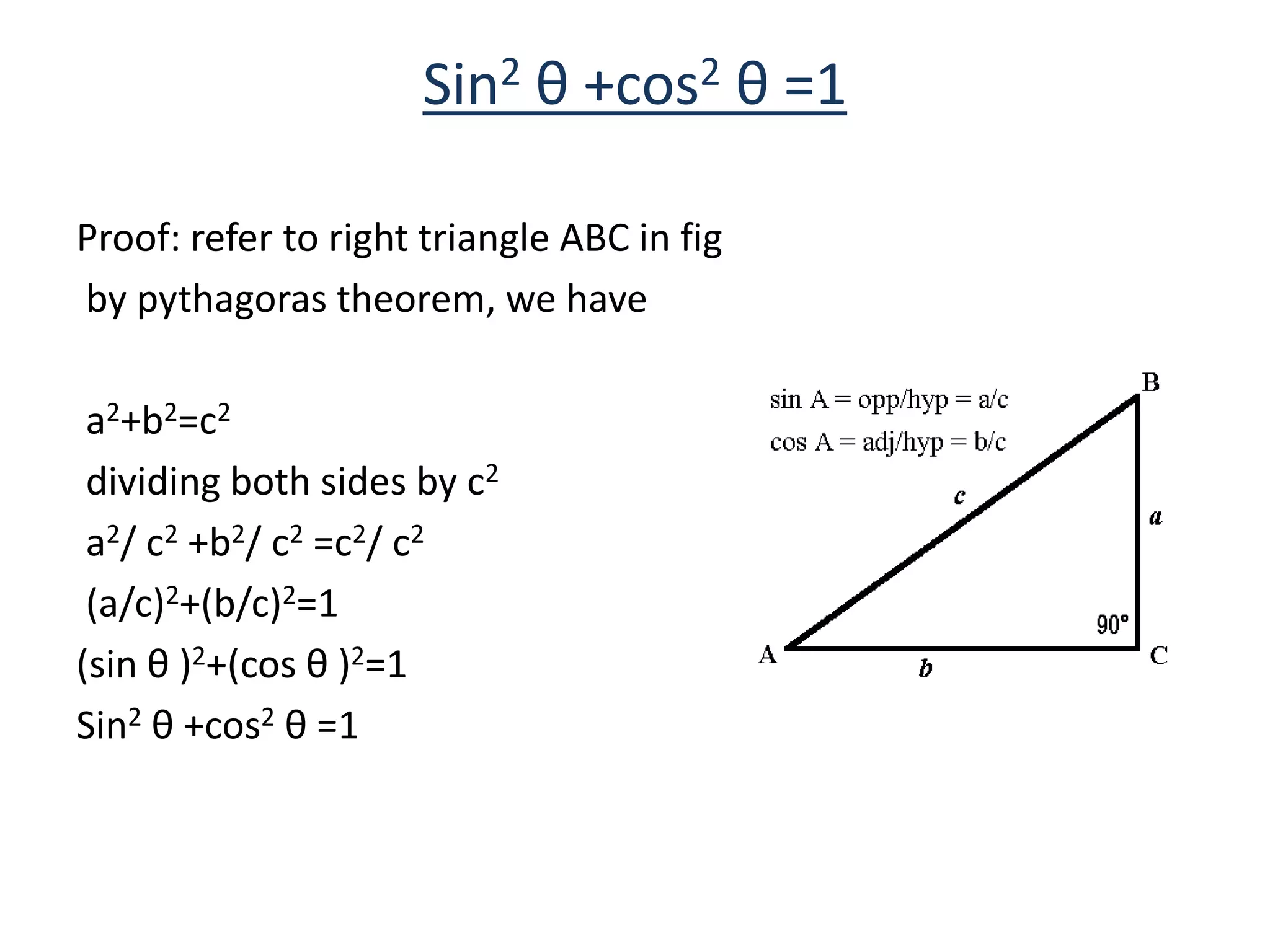- Fundamental trigonometric identities are derived, including that sine squared plus cosine squared equals one.

1. INTRODUCTION TO
TRIGONOMETRY
Nayyab Imdad

2. Format of Talk
• INTRODUCTION
• CONCEPT OF AN ANGLE
• TRIGONOMETRIC FUNCTIONS

3. INTRODUCTION
• The word ‘TRIGONOMETRY’ is the combination of three
Greek words:
Trei (three)
Goni (angles) and
Metron (measurement).
Literally it means measurement of triangle.
• It is an important branch of Mathematics that studies
triangles and the relationship between their sides and the
angles.

4. Concept of an Angle
• Two rays with a common starting point
form an angle: one of the rays of angle is
called initial side and the other as
terminal side.
• An angle is said to be positive/negative if
the rotation is anti-clockwise/clockwise.
Angles are usually denoted by Greek
letters such as α(alpha),β(beta) ,
γ(gamma) , Θ (theta) etc.

5. Degrees and radians
A degree is a measurement of plane angle, representing 1⁄360 of a full rotation,
usually denoted by the symbol “ °“
1 full rotation = 360 ° ½ rotation = 180 ° ¼ rotation = 90 °

6. A radian is the measure of the angle
subtended at the center of the circle
by an arc, whose length is equal to
the radius of the circle.
Degrees and radians

7. Sexagesimal system
• A number system with base 60. It uses the concept
of degrees, minutes and seconds for measuring angles.
Thus
1 rotation(anti-clockwise)=360 °
One degree(1 °)=60’
One minute(1’)=60”

8. Example1:convert 18 ° 6’21” to decimal
form.
Solution: 1’=(1/60) ° and 1”=(1/60)’=(1/60X60) °
18 ° 6’21” =(18+6(1/60)+21(1/60X60)) °
=(18+0.1+0.005833) °
=18.105833 °

9. Example2: convert 21.256 ° to the D °M’S”
form.
SOLUTION:
21.256 ° =21 °+0.256 °
=21 °+15.36 ‘ : 0.256 =(0.256)(1 °)
=21 °+15’+0.36’ =(0.256)(60’)
=21 °+15’+0.36’ =15.36’
=21 °+15’+21.6” : 0.36’=(0.36)(1’)
=21 °+15’+21.6” =(0.36)(60”)
=21°15’22” =21.6”

10. TRIGONOMETRIC FUNCTIONS
• The side AB opposite to 90 °
is called hypotenuse (hyp).
• The side BC opposite to Θ
(theta) is called the
opposite (opp).
• The side AC related to angle
Θ is called the adjacent
(adj).

11. • There are six ways to form ratios of the three sides of a
triangle, summarize as follows:
Sine θ :sin(θ)=opp/hyp
Cosine θ :cos(θ)=adj/hyp
Tangent θ :tan(θ)=opp/adj
Cosecant θ :csc(θ)=hyp/opp
Secant θ :sec(θ)=hyp/adj
Cotangent θ :cot(θ)=adj/opp

12. FUNDAMENTAL IDENTITIES
For any real number θ, we shall derive the following three fundamental
identities:
1)Sin2 θ +cos2 θ =1
2)1+tan2 θ = sec2 θ
3)1+cot2 θ =csc2 θ

13. Sin2 θ +cos2 θ =1
Proof: refer to right triangle ABC in fig
by pythagoras theorem, we have
a2+b2=c2
dividing both sides by c2
a2/ c2 +b2/ c2 =c2/ c2
(a/c)2+(b/c)2=1
(sin θ )2+(cos θ )2=1
Sin2 θ +cos2 θ =1

14. Thank You Very Much
Any Questions ?