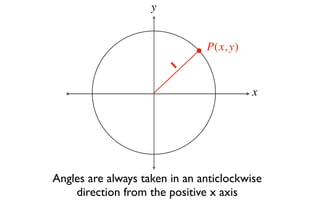
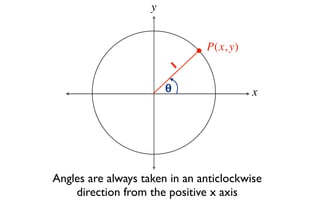
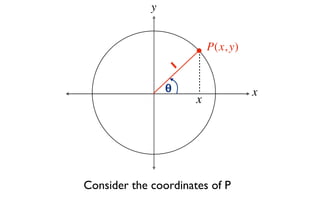
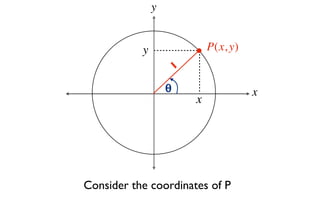
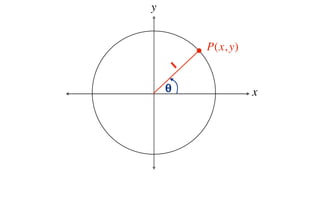
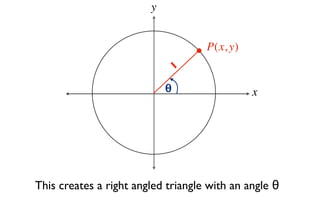
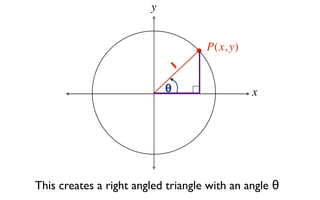
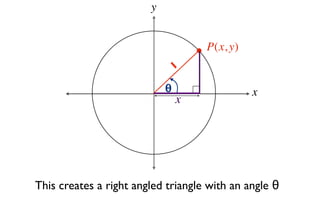
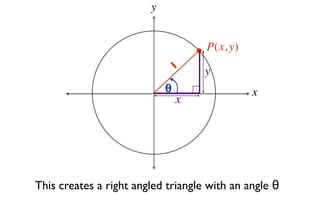
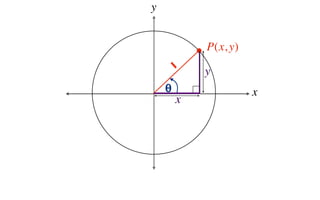
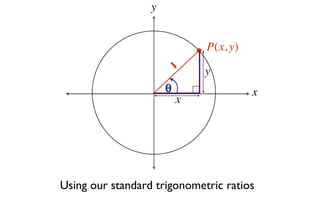
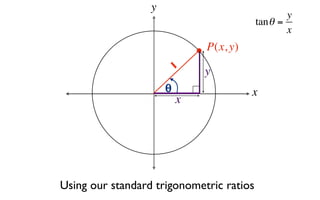
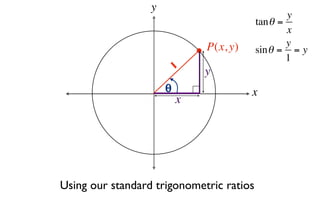
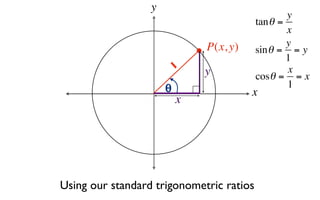
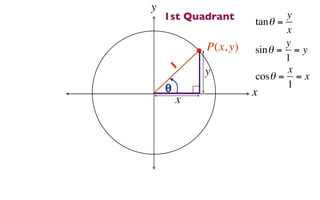
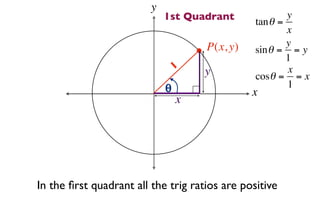
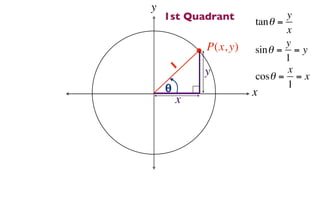
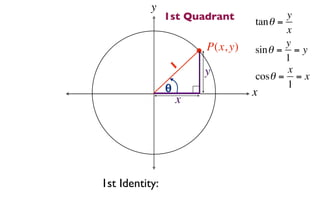
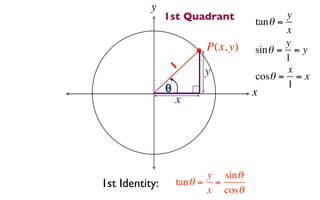
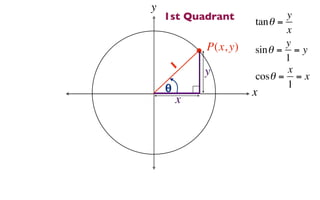
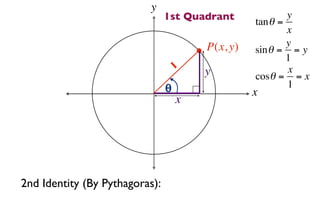
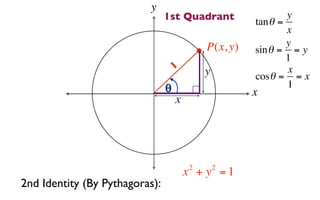
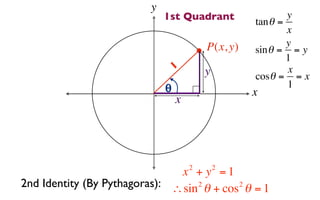
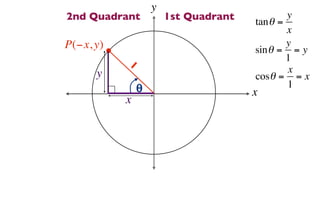
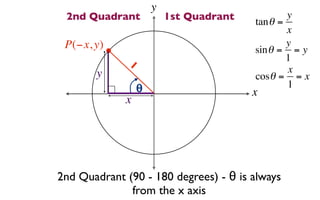
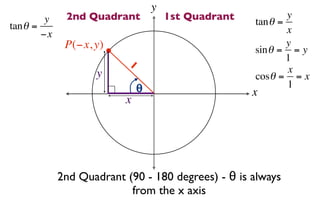
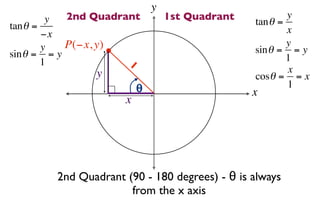
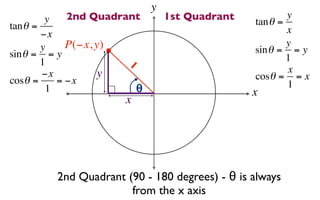
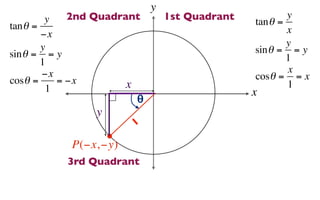
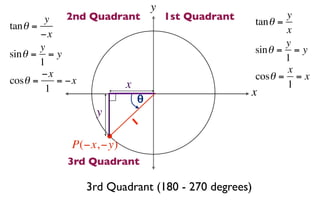
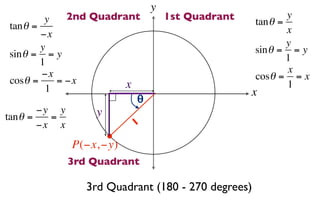
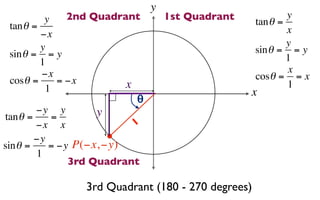
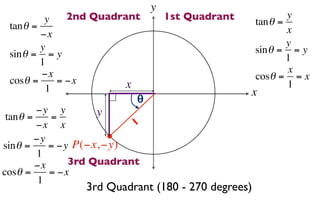
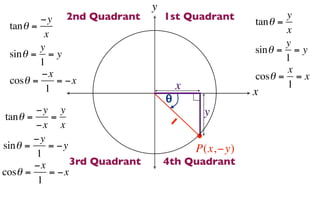
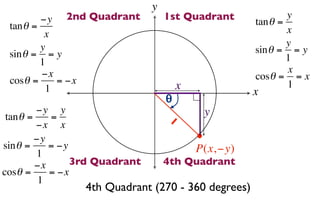
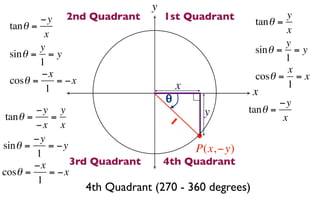
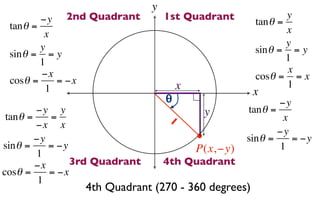
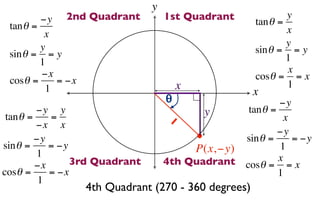
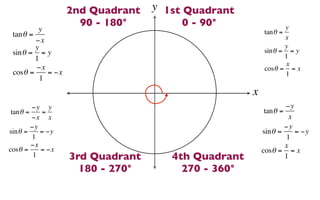
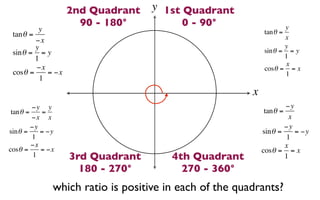
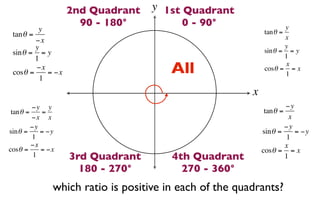
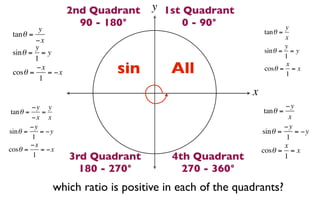
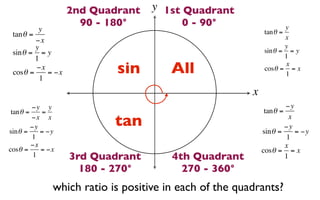
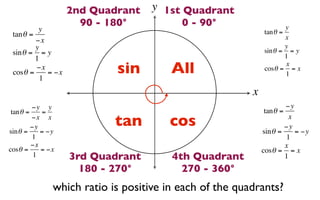
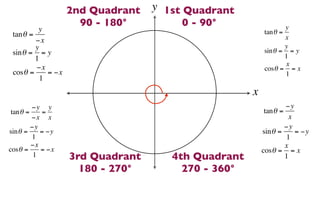
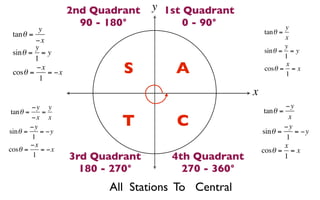
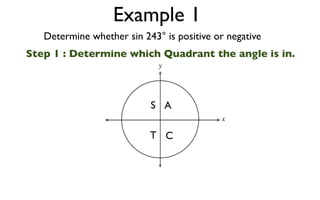
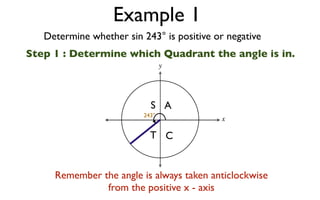
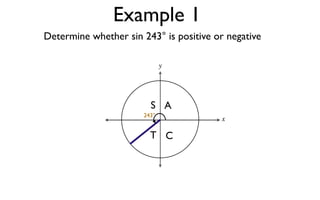
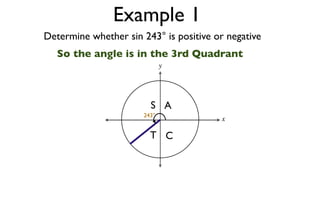
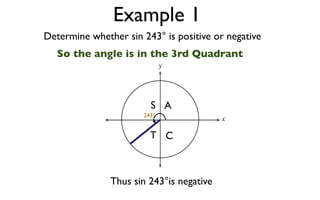
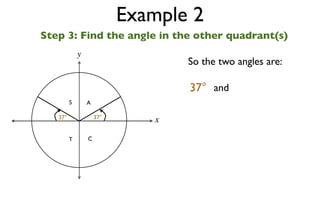
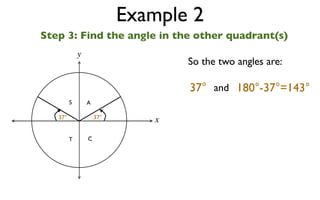
The document discusses trigonometric functions on the unit circle. It defines trig ratios for angles in each of the four quadrants using right triangles formed with the point (x,y) and the origin. Key identities presented are: 1) tanθ = sinθ/cosθ 2) sin2θ + cos2θ = 1 The signs of the trig functions depend on the quadrant, with trig ratios being positive in Quadrant I and changing appropriately in other quadrants based on the signs of x and y.

1. Trig on the Unit Circle
Monday 23rd May 2011

2. y
P(x, y)
1
x

3. y
P(x, y)
1
x

4. y
P(x, y)
1
x
Angles are always taken in an anticlockwise
direction from the positive x axis

5. y
P(x, y)
1
θ x
Angles are always taken in an anticlockwise
direction from the positive x axis

6. y
P(x, y)
1
θ x

7. y
P(x, y)
1
θ x
Consider the coordinates of P

8. y
P(x, y)
1
θ x
x
Consider the coordinates of P

9. y
y P(x, y)
1
θ x
x
Consider the coordinates of P

10. y
P(x, y)
1
θ x

11. y
P(x, y)
1
θ x
This creates a right angled triangle with an angle θ

12. y
P(x, y)
1
θ x
This creates a right angled triangle with an angle θ

13. y
P(x, y)
1
θ x
x
This creates a right angled triangle with an angle θ

14. y
P(x, y)
1 y
θ x
x
This creates a right angled triangle with an angle θ

15. y
P(x, y)
1 y
θ x
x

16. y
P(x, y)
1 y
θ x
x
Using our standard trigonometric ratios

17. y
y
tan θ =
x
P(x, y)
1 y
θ x
x
Using our standard trigonometric ratios

18. y
y
tan θ =
x
P(x, y) y
sin θ = = y
1
1 y
θ x
x
Using our standard trigonometric ratios

19. y
y
tan θ =
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
Using our standard trigonometric ratios

20. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x

21. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
In the first quadrant all the trig ratios are positive

22. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x

23. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
1st Identity:

24. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
y sin θ
1st Identity: tan θ = =
x cosθ

25. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x

26. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
2nd Identity (By Pythagoras):

27. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
2 2
x + y =1
2nd Identity (By Pythagoras):

28. y
1st Quadrant tan θ =
y
x
P(x, y) y
sin θ = = y
1
1 y x
cosθ = = x
θ 1
x
x
2 2
x + y =1
2nd Identity (By Pythagoras): ∴sin 2 θ + cos 2 θ = 1

29. Two important Trig Identities

30. Two important Trig Identities
sin θ
tan θ =
cosθ

31. Two important Trig Identities
sin θ
tan θ =
cosθ
2 2
sin θ + cos θ = 1

32. y
2nd Quadrant 1st Quadrant tan θ =
y
x
P(−x, y) y
sin θ = = y
1 1
y x
cosθ = = x
θ 1
x
x

33. y
2nd Quadrant 1st Quadrant tan θ =
y
x
P(−x, y) y
sin θ = = y
1 1
y x
cosθ = = x
θ 1
x
x
2nd Quadrant (90 - 180 degrees) - θ is always
from the x axis

34. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
P(−x, y) y
sin θ = = y
1 1
y x
cosθ = = x
θ 1
x
x
2nd Quadrant (90 - 180 degrees) - θ is always
from the x axis

35. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y P(−x, y) y
sin θ = = y sin θ = = y
1 1 1
y x
cosθ = = x
θ 1
x
x
2nd Quadrant (90 - 180 degrees) - θ is always
from the x axis

36. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y P(−x, y) y
sin θ = = y sin θ = = y
1 1 1
−x y x
cosθ = = −x cosθ = = x
1 θ 1
x
x
2nd Quadrant (90 - 180 degrees) - θ is always
from the x axis

37. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
y 1
P(−x, −y)
3rd Quadrant

38. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
y 1
P(−x, −y)
3rd Quadrant
3rd Quadrant (180 - 270 degrees)

39. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y y y
tan θ = = 1
−x x
P(−x, −y)
3rd Quadrant
3rd Quadrant (180 - 270 degrees)

40. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y y y
tan θ = = 1
−x x
−y
sin θ = = −y P(−x, −y)
1
3rd Quadrant
3rd Quadrant (180 - 270 degrees)

41. y
y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y y y
tan θ = = 1
−x x
−y
sin θ = = −y P(−x, −y)
1
−x 3rd Quadrant
cosθ = = −x
1
3rd Quadrant (180 - 270 degrees)

42. y
−y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y y y
tan θ = = 1
−x x
−y
sin θ = = −y P(x, −y)
1
−x 3rd Quadrant 4th Quadrant
cosθ = = −x
1

43. y
−y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y y y
tan θ = = 1
−x x
−y
sin θ = = −y P(x, −y)
1
−x 3rd Quadrant 4th Quadrant
cosθ = = −x
1
4th Quadrant (270 - 360 degrees)

44. y
−y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y
−y y y tan θ =
tan θ = = 1 x
−x x
−y
sin θ = = −y P(x, −y)
1
−x 3rd Quadrant 4th Quadrant
cosθ = = −x
1
4th Quadrant (270 - 360 degrees)

45. y
−y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y
−y y y tan θ =
tan θ = = 1 x
−x x
−y
−y sin θ = = −y
sin θ = = −y P(x, −y) 1
1
−x 3rd Quadrant 4th Quadrant
cosθ = = −x
1
4th Quadrant (270 - 360 degrees)

46. y
−y 2nd Quadrant 1st Quadrant tan θ =
y
tan θ = x
x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = −x cosθ = = x
1 x 1
θ x
−y
−y y y tan θ =
tan θ = = 1 x
−x x
−y
−y sin θ = = −y
sin θ = = −y P(x, −y) 1
1
−x 3rd Quadrant 4th Quadrant cosθ = x = x
cosθ = = −x 1
1
4th Quadrant (270 - 360 degrees)

47. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = x
cosθ = = −x 1
1
x
−y y −y
tan θ = = tan θ =
−x x x
−y −y
sin θ = = −y sin θ = = −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°

48. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = x
cosθ = = −x 1
1
x
−y y −y
tan θ = = tan θ =
−x x x
−y −y
sin θ = = −y sin θ = = −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
which ratio is positive in each of the quadrants?

49. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
cosθ =
−x
1
= −x All x
cosθ = = x
1
x
−y y −y
tan θ = = tan θ =
−x x x
−y −y
sin θ = = −y sin θ = = −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
which ratio is positive in each of the quadrants?

50. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
cosθ =
−x
1
= −x sin All x
cosθ = = x
1
x
−y y −y
tan θ = = tan θ =
−x x x
−y −y
sin θ = = −y sin θ = = −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
which ratio is positive in each of the quadrants?

51. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
cosθ =
−x
1
= −x sin All x
cosθ = = x
1
x
−y y −y
tan θ = = tan θ =
sin θ =
−x x
−y
= −y
tan sin θ =
−y
x
= −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
which ratio is positive in each of the quadrants?

52. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
cosθ =
−x
1
= −x sin All x
cosθ = = x
1
x
−y y −y
tan θ = = tan θ =
sin θ =
−x x
−y
= −y
tan cos sin θ =
−y
x
= −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
which ratio is positive in each of the quadrants?

53. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
−x x
cosθ = = x
cosθ = = −x 1
1
x
−y y −y
tan θ = = tan θ =
−x x x
−y −y
sin θ = = −y sin θ = = −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°

54. 2nd Quadrant y 1st Quadrant
90 - 180° 0 - 90° y
y tan θ =
tan θ = x
−x
y y
sin θ = = y sin θ = = y
1 1
cosθ =
−x
1
= −x S A x
cosθ = = x
1
x
−y y −y
tan θ = = tan θ =
sin θ =
−x x
−y
= −y
T C sin θ =
−y
x
= −y
1 1
−x x
cosθ = = −x cosθ = = x
1 3rd Quadrant 4th Quadrant 1
180 - 270° 270 - 360°
All Stations To Central

55. Example 1
Determine whether sin 243° is positive or negative

56. Example 1
Determine whether sin 243° is positive or negative
Step 1 : Determine which Quadrant the angle is in.

57. Example 1
Determine whether sin 243° is positive or negative
Step 1 : Determine which Quadrant the angle is in.
y
S A
x
T C

58. Example 1
Determine whether sin 243° is positive or negative
Step 1 : Determine which Quadrant the angle is in.
y
S A
x
T C
Remember the angle is always taken anticlockwise
from the positive x - axis

59. Example 1
Determine whether sin 243° is positive or negative
Step 1 : Determine which Quadrant the angle is in.
y
S A
243°
x
T C
Remember the angle is always taken anticlockwise
from the positive x - axis

60. Example 1
Determine whether sin 243° is positive or negative
y
S A
243°
x
T C

61. Example 1
Determine whether sin 243° is positive or negative
So the angle is in the 3rd Quadrant
y
S A
243°
x
T C

62. Example 1
Determine whether sin 243° is positive or negative
So the angle is in the 3rd Quadrant
y
S A
243°
x
T C
Thus sin 243°is negative

63. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6

64. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)

65. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)
∴θ = 37° (to nearest degree from Calculator)

66. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)
∴θ = 37° (to nearest degree from Calculator)
Step 2: Find other quadrants where the ratio is positive

67. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)
∴θ = 37° (to nearest degree from Calculator)
Step 2: Find other quadrants where the ratio is positive
y
S A
x
T C

68. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)
∴θ = 37° (to nearest degree from Calculator)
Step 2: Find other quadrants where the ratio is positive
y
S A As sin is positive it must be an
angle in the 1st or 2nd Quadrant
x
T C

69. Example 2
For 0 ≤θ≤360° find all possible values of θ such that
sin θ = 0.6
Step 1: Find the corresponding acute angle (i.e in the 1st Q)
∴θ = 37° (to nearest degree from Calculator)
Step 2: Find other quadrants where the ratio is positive
y
S A As sin is positive it must be an
angle in the 1st or 2nd Quadrant
x
T C
Step 3: Find the angle in the other quadrant(s)

70. Example 2
y
S A
37° 37°
x
T C

71. Example 2
Step 3: Find the angle in the other quadrant(s)
y
S A
37° 37°
x
T C

72. Example 2
Step 3: Find the angle in the other quadrant(s)
y
So the two angles are:
37° and
S A
37° 37°
x
T C

73. Example 2
Step 3: Find the angle in the other quadrant(s)
y
So the two angles are:
37° and 180°-37°=143°
S A
37° 37°
x
T C