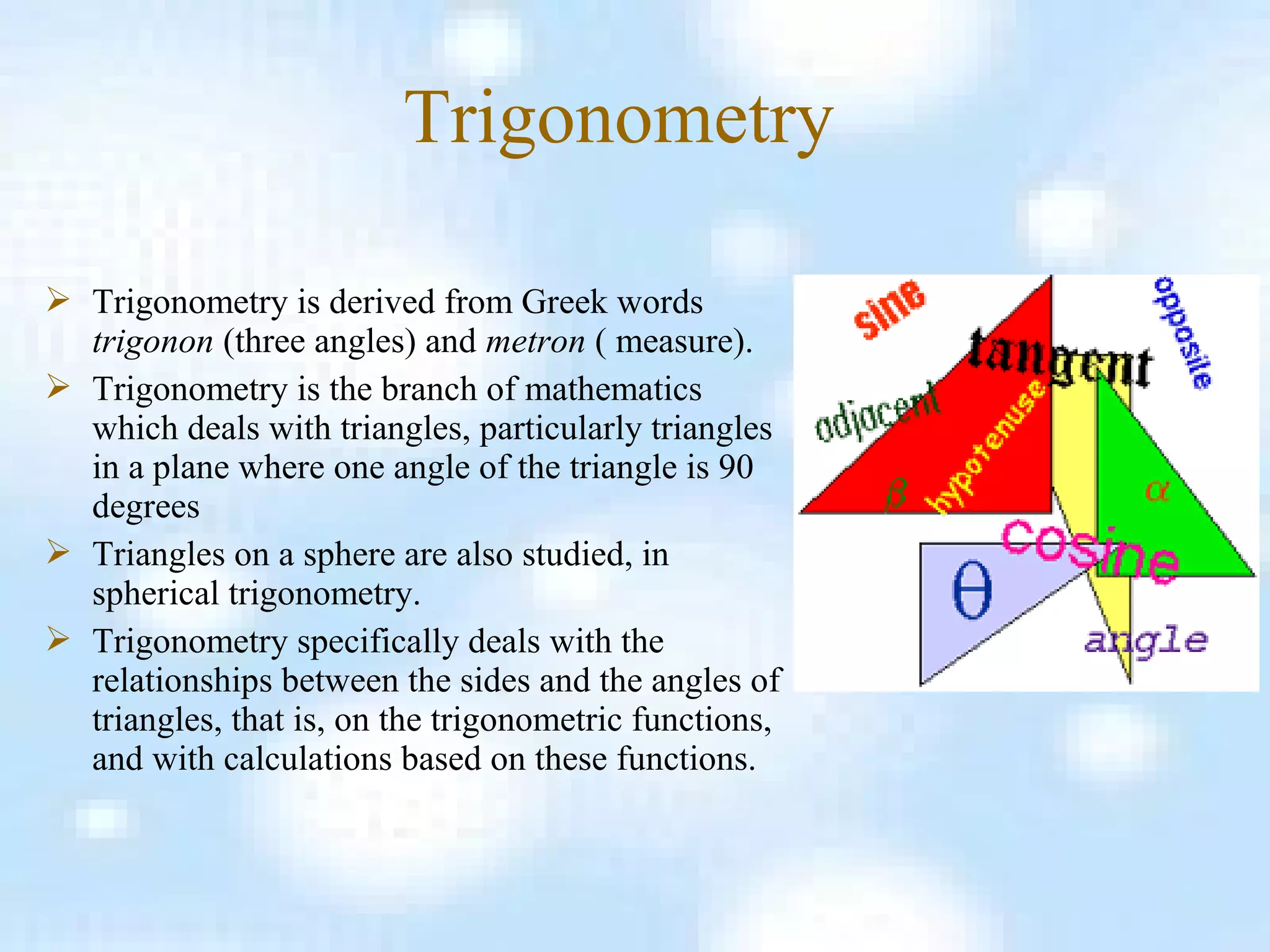
Trigonometry is a branch of mathematics focused on the relationships between the angles and sides of triangles, particularly right triangles. It involves concepts such as the Pythagorean theorem and various trigonometric ratios including sine, cosine, and tangent. The document also includes specific values of trigonometric functions for common angles and definitions related to right triangles.

1. TRIGONOMETR
Y

2.  Trigonometry is derived from Greek words
trigonon (three angles) and metron ( measure).
 Trigonometry is the branch of mathematics
which deals with triangles, particularly triangles
in a plane where one angle of the triangle is 90
degrees
 Triangles on a sphere are also studied, in
spherical trigonometry.
 Trigonometry specifically deals with the
relationships between the sides and the angles of
triangles, that is, on the trigonometric functions,
and with calculations based on these functions.
Trigonometry

3. Right Triangle
 A triangle in which one angle
is equal to 90° is called right
triangle.
 The side opposite to the right
angle is known as hypotenuse.
AB is the hypotenuse
 The other two sides are
known as legs.
AC and BC are the legs
Trigonometry deals with Right Triangles

4. Pythagoras Theorem
In any right triangle, the area of the square whose
side is the hypotenuse is equal to the sum of areas of
the squares whose sides are the two legs.
In the figure
AB2
= BC2
+ AC2

5. Trigonometry
Trigonometry is the branch of mathematics that looks
at the relationship between the length of the sides
and the angles in a right angled triangle.
It helps us calculate the length of unknown sides,
without drawing the triangle, and it also helps us
calculate the size of an unknown angle without having
to measure it.
Let us look at a right angle triangle.

6. Trigonometry
O F
C
Hypotenuse
x0
Opposite
Adjacent
O F
C
Hypotenuse
y0
Opposite
Adjacent
The ‘Hypotenuse’ is always
opposite the right angle
The ‘Opposite’ is always
opposite the angle under
investigation.
The ‘Adjacent’ is always
alongside the angle under
investigation.

7. Adjacent , Opposite Side andAdjacent , Opposite Side and
Hypotenuse of a Right Angle TriangleHypotenuse of a Right Angle Triangle..

8. Adjacent side
Oppositeside
θθ
hypotenuse

9. φ
hypotenuse
Adjacentside
Opposite side

10. Definition of Sine Ratio.
θθ
For any right-angled triangle
Sinθ =
Opposite side
hypotenuses

11. Definition of Cosine Ratio.
θθ
For any right-angled triangle
Cosθ =
hypotenuses
Adjacent Side

12. Definition of Tangent Ratio.
θθ
For any right-angled triangle
tanθ =
Adjacent Side
Opposite Side

13. ConclusionConclusion
hypotenuse
sideopposite
sin =θ
hypotenuse
sidedjacenta
cos =θ
sidedjacenta
sideopposite
tan =θ
Make Sure
that the
triangle is
right-angled

14. 14
Trigonometric ratios
Sine(sin) opposite side/hypotenuse
Cosine(cos) adjacent side/hypotenuse
Tangent(tan) opposite side/adjacent side
Cosecant(cosec) hypotenuse/opposite side
Secant(sec) hypotenuse/adjacent side
Cotangent(cot) adjacent side/opposite side

15. 15
Values of trigonometric function
of Angle A
sinθ = a/c
cosθ = b/c
tanθ = a/b
cosecθ = c/a
secθ = c/b
cotθ = b/a

16. 16
Values of Trigonometric function
0 30 45 60 90
Sine 0 0.5 1/√2 √3/2 1
Cosine 1 √3/2 1/√2 0.5 0
Tangent 0 1/ √3 1 √3 Not defined
Cosecant Not defined 2 √2 2/ √3 1
Secant 1 2/ √3 √2 2 Not defined
Cotangent Not defined √3 1 1/ √3 0

17. CONTEMPTORY
ANGLES

18. DONE BY – AARUSHI
,AMI,UNNATI &VIDHI