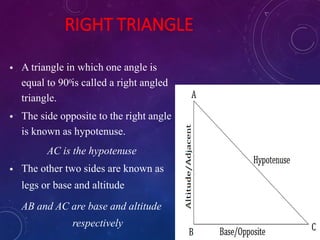
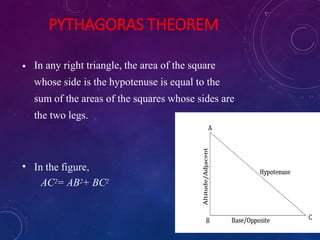
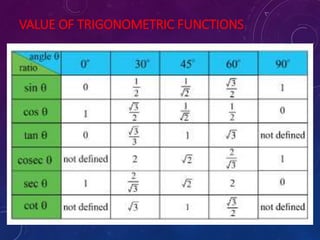
This document provides an overview of trigonometry. It defines trigonometry as dealing with relationships between sides and angles of triangles, particularly right triangles. The origins of trigonometry can be traced back 4000 years to ancient civilizations. Key concepts discussed include right triangles, the Pythagorean theorem, trigonometric ratios like sine, cosine and tangent, and applications of trigonometry in fields like construction, astronomy, and engineering. Examples are provided for using trigonometric functions to solve problems involving heights and distances.