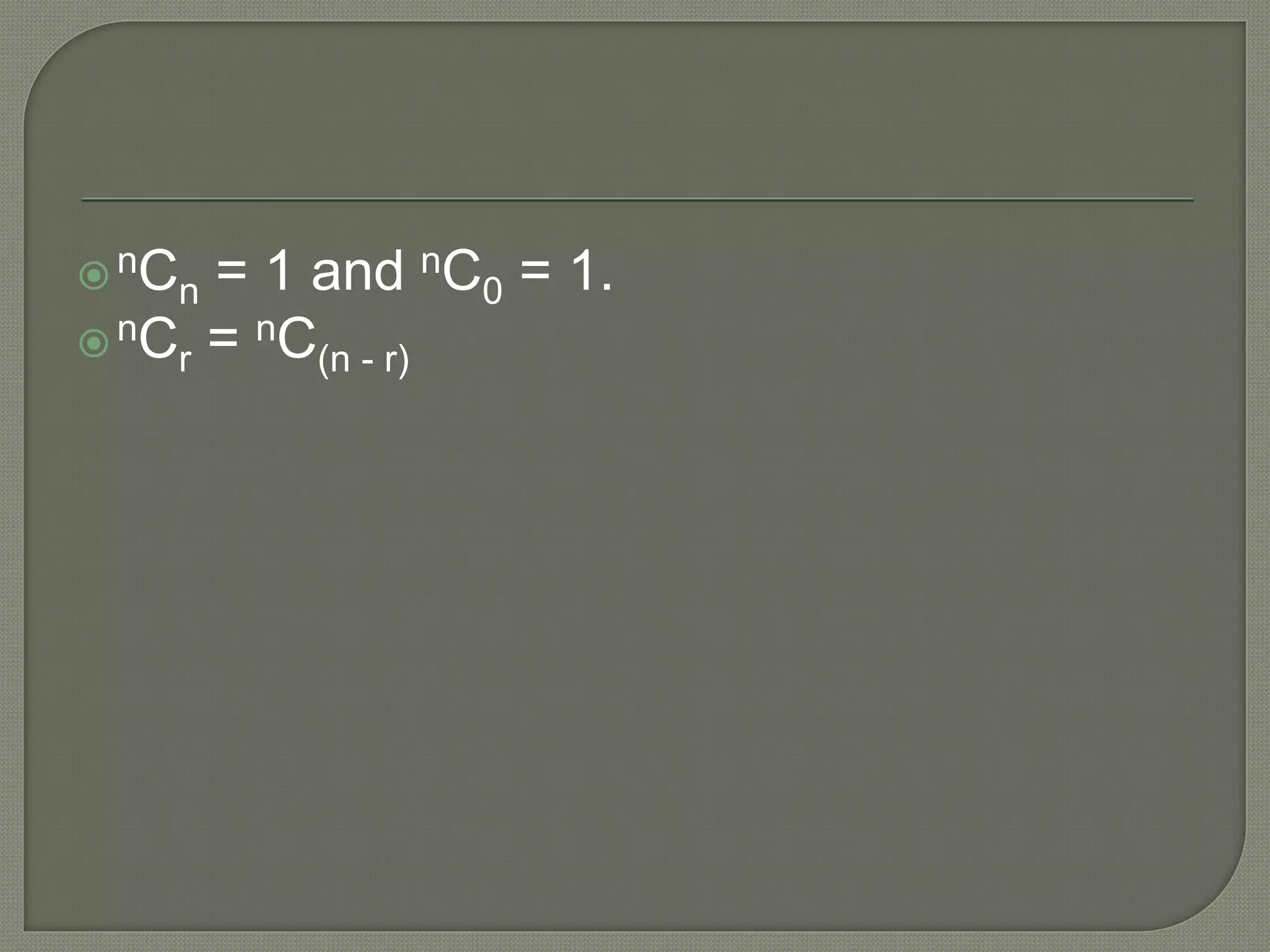The document discusses permutations, combinations, and probability. It provides examples and formulas for calculating the number of permutations of objects taken a certain number at a time. It also discusses combinations and provides examples. The document then provides several word problems involving permutations, combinations, and calculating probabilities of events occurring.

2. The different arrangements of a given
number of things by taking some or all at a
time, are called permutations.
Examples:
• All permutations (or arrangements) made with the
letters a, b, c by taking two at a time are
(ab, ba, ac, ca, bc, cb).
• All permutations made with the
letters a, b, c taking all at a time are:
( abc, acb, bac, bca, cab, cba)

3. Number of all permutations of n things,
taken r at a time, is given by:
nPr = n(n - 1)(n - 2) ... (n - r + 1) =n!(n - r)!
Examples:
6P2 = (6 x 5) = 30.
7P3 = (7 x 6 x 5) = 210.
Cor. number of all permutations
of n things, taken all at a time = n!.

4. If there are n subjects of which p1 are alike
of one kind; p2 are alike of another
kind;p3 are alike of third kind and so on
and pr are alike of rth kind,
such that (p1 + p2 + ... pr) = n.
Then, number of permutations of
these n objects is =n!/((p1!).(p2)!.....(pr!))

5.  Each of the different groups or selections
which can be formed by taking some or all of
a number of objects is called a combination.
 Examples:
 Suppose we want to select two out of three
boys A, B, C. Then, possible selections are
AB, BC and CA.
 Note: AB and BA represent the same
selection.

6. nCn = 1 and nC0 = 1.
nCr = nC(n - r)

7. From a group of 7 men and 6 women, five
persons are to be selected to form a
committee so that at least 3 men are there
on the committee. In how many ways can
it be done?

8. In how many different ways can the letters
of the word 'LEADING' be arranged in
such a way that the vowels always come
together?
In how many ways can the letters of the
word 'LEADER' be arranged?

9. How many 4-letter words with or without
meaning, can be formed out of the letters
of the word, 'LOGARITHMS', if repetition of
letters is not allowed?
How many 3-digit numbers can be formed
from the digits 2, 3, 5, 6, 7 and 9, which
are divisible by 5 and none of the digits is
repeated?

10.  When we throw a coin, then either a Head (H) or a Tail
(T) appears.
 A dice is a solid cube, having 6 faces, marked 1, 2, 3,
4, 5, 6 respectively. When we throw a die, the outcome
is the number that appears on its upper face.
 A pack of cards has 52 cards.
 It has 13 cards of each suit, name Spades, Clubs,
Hearts and Diamonds.
 Cards of spades and clubs are black cards.
 Cards of hearts and diamonds are red cards.
 There are 4 honours of each unit.
 There are Kings, Queens and Jacks. These are all
called face cards.

11. Tickets numbered 1 to 20 are mixed up
and then a ticket is drawn at random. What
is the probability that the ticket drawn has
a number which is a multiple of 3 or 5?
A bag contains 2 red, 3 green and 2 blue
balls. Two balls are drawn at random.
What is the probability that none of the
balls drawn is blue?

12. Three unbiased coins are tossed. What is
the probability of getting at most two
heads?
In a class, there are 15 boys and 10 girls.
Three students are selected at random.
The probability that 1 girl and 2 boys are
selected, is

13. In a lottery, there are 10 prizes and 25
blanks. A lottery is drawn at random. What
is the probability of getting a prize?
Two cards are drawn together from a pack
of 52 cards. The probability that one is a
spade and one is a heart, is:

14.  You roll two dice. The first die shows a ONE
and the other die rolls under the table and
you cannot see it. Now, what is the
probability that both die show ONE?
 A new bag of golf tees contains 10 red tees,
10 orange tees, 10 green tees and 10 blue
tees. You empty the tees into your golf
bag. What is the probability of grabbing out
two tees of the same color in a row for you
and your partner?