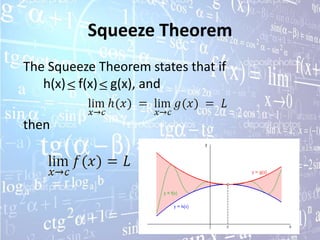
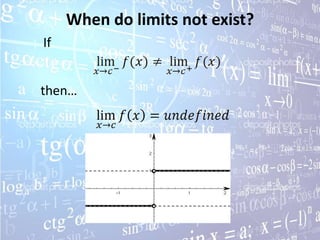The document discusses limits and continuity, explaining what limits are, how to evaluate different types of limits using techniques like direct substitution, dividing out, and rationalizing, and how limits relate to concepts like derivatives, continuity, discontinuities, and the intermediate value theorem. Special trig limits, properties of limits, and how limits can be used to find derivatives are also covered.

1. Limits and Continuity
Thu Mai, Michelle Wong,
Tam Vu

2. What are Limits?
Limits are built upon the concept of infinitesimal.
Instead of evaluating a function at a certain x-value,
limits ask the question, “What value does a function
approaches as its input and a constant becomes
infinitesimally small?” Notice how this question does
not depend upon what f(c) actually is. The notations
for writing a limit as x approaches a constant of the
function f(x) is:
Where c is the constant and L (if it is defined) is the
value that the function approaches.

3. Evaluating Limits: Direct Substitution
Sometimes, the limit as x approaches c of f(x)
is equal to f(c). If this is the case, just directly
substitute in c for x in the limit expression, as
shown below.

4. Dividing Out Technique
1. Always start by seeing if the substitution method works.
2. If, when you do so, the new expression obtained is an indeterminate form such as
0/0… try the dividing out technique!
3. Because both the numerator an denominator are 0, you know they share a similar
factor.
4. Factor whatever you can in the given function.
5. If there is a matching factor in the numerator and denominator, you can cross thru
them since they “one out.”
6. With your new, simplified function attempt the substitution method again. Plug
whatever value x is approaching in for x.
7. The answer you arrive at is the limit.
*Note: You may need to algebraically manipulate the function.

5. Rationalizing
Sometimes, you will come across limits with radicals in fractions.
Steps
1. Use direct substitution by plugging in zero for x.
2. If you arrive at an undefined answer (0 in the denominator) see if there are any
obvious factors you could divide out.
3. If there are none, you can try to rationalize either the numerator or the
denominator by multiplying the expression with a special form of 1.
4. Simplify the expression. Then evaluate the rewritten limit.
Ex:

6. Squeeze Theorem
The Squeeze Theorem states that if
h(x) f(x) g(x), and
then

7. Special Trig Limits
(memorize these)
h is angle in radians
area of blue: cos(h)sin(h)/2
area of pink: h/2
area of yellow: tan(h)/2
Since
by the Squeeze Theorem we can say that

8. Special Trig Limits Continued

9. Continuity and Discontinuity
A function is continuous in the interval [a,b] if
there does not exist a c in the interval [a,b]
such that:
1) f(c) is undefined, or
2) , or 3)
The following functions are discontinuous b/c they do not fulfill ALL
the properties of continuity as defined above.

10. Removable vs Non-removable
Discontinuities
• A removable discontinuity exists at c if f can be made continuous by
redefining f(c).
• If there is a removable discontinuity at c, the limit as xc exists;
likewise if there is a non-removable discontinuity at c, the limit as xc
does not exist.
For this function, there is a removable discontinuity
at x=3; f(3) = 4 can simply be redefined as f(3) = 2
to make the function continuous. The limit as x3
exists.
For this function, there is a non-removable
discontinuity at x=3; even if f(3) is redefined, the
function will never be continuous. The limit as x3
does not exist.

11. Intermediate Value Theorem
The Intermediate Value Theorem states that if
f(x) is continuous in the closed interval [a,b]
and f(a) M f(b), then at least one c exists in
the interval [a,b] such that:
f(c) = M

12. When do limits not exist?
If
then…

13. Vertical Asymptotes
f(x) and g(x) are continuous on an open interval
containing c. if f(c) is not equal to 0 and g(c)= 0
and there’s an open interval with c which g(x) is
not 0 for all values of x that are not c, then…..
There is an asymptote at x = c
for

14. Properties of Limits
Let b and c be real numbers, n be a positive integer, f and g be functions
with the following limits.
Sum or Difference Quotient
Scalar Multiple Power
Product

15. Limits Substitution
With limits substitution (informally named so
by yours truly), if
then
This is useful for evaluating limits such as:

16. How Do Limits Relate to
Derivatives?
What is a derivative?
• The derivative of a function is defined as that function’s INSTANT rate of change.
Applying Prior Knowledge:
• As learned in pre-algebra, the rate of change of a function is defined by: Δy
Δx
Apply Knowledge of Limits:
• Consider that a limit describes the behavior of a function as x gets closer and
closer to a point on a function from both left and right.
• Δy describes a function’s rate of change. To find the function’s INSTANT rate of
Δx change, we can use limits.
• We can take:
lim Δy
Δx 0 Δx
WHY? As the change in x gets closer and closer to 0, we can more
accurately predict the function’s INSTANT rate of change, and thus the function’s
derivative.

17. How Do Limits Relate to
Derivatives?
Δy y –y
Consider that Δx can be rewritten as 2Δx 1 .
(x+ Δx, f(x+ Δx)) Analyze the graph. Notice that the change
(x, f(x)) in y between any two points on a function is
f(x+ Δx) – f(x). Thus:
Δy = y2 – y1 = f(x+ Δx) – f(x)
Δx Δx Δx
So lim Δy can be rewritten as lim f(x+ Δx) – f(x) .
Δx 0 Δx Δx0 Δx
Therefore, the derivative of f(x) at x is given by:
lim f(x+ Δx) – f(x)
Δx 0 Δx