This document provides an overview of fundamentals of trigonometry including:
- There are two main types of trigonometry - plane and spherical trigonometry. Plane trigonometry deals with angles and triangles in a plane, while spherical trigonometry deals with triangles on a sphere.
- An angle is defined as the union of two rays with a common endpoint, and can be measured in degrees or radians. There are four quadrants used to classify angles in the Cartesian plane.
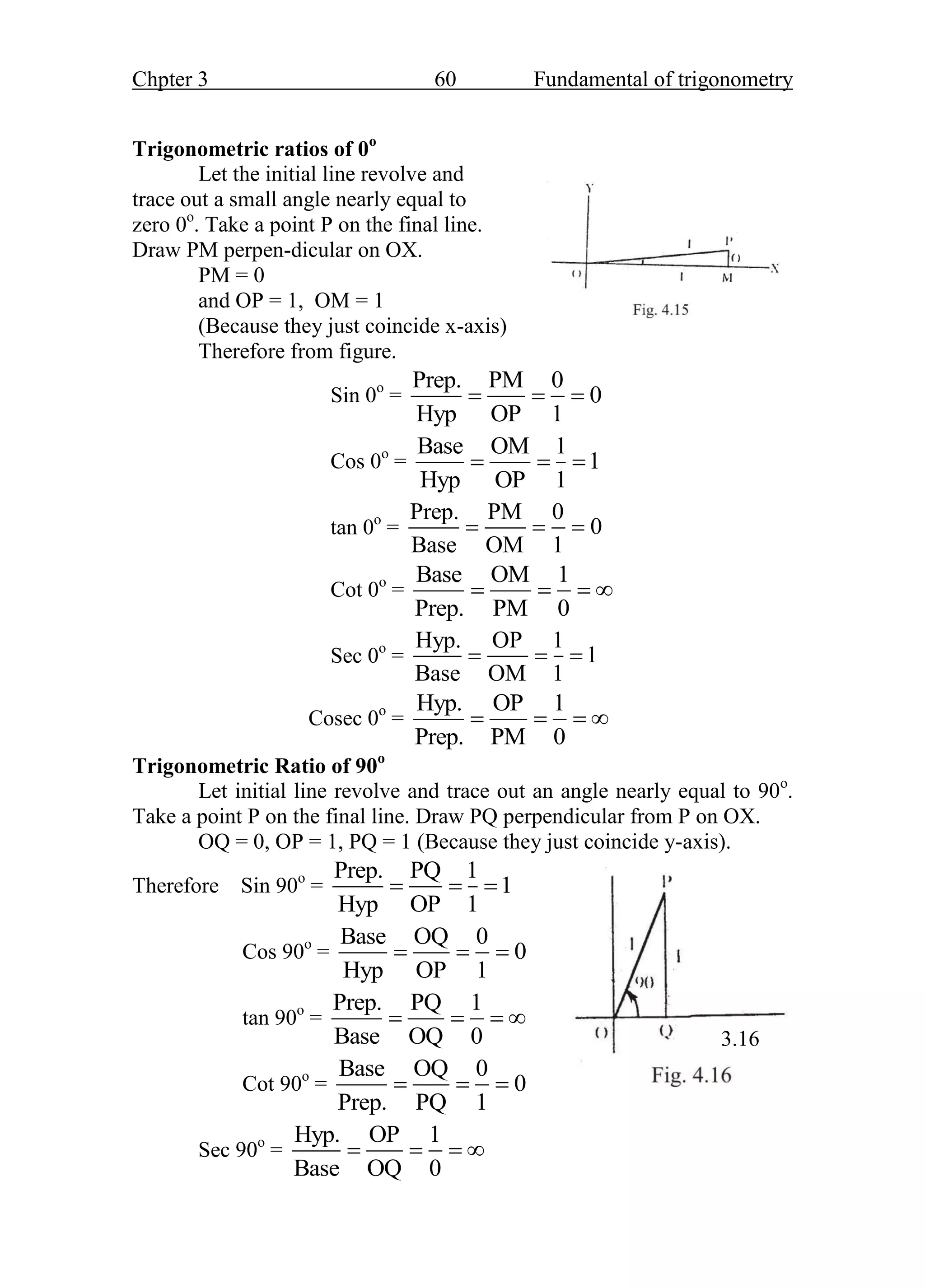
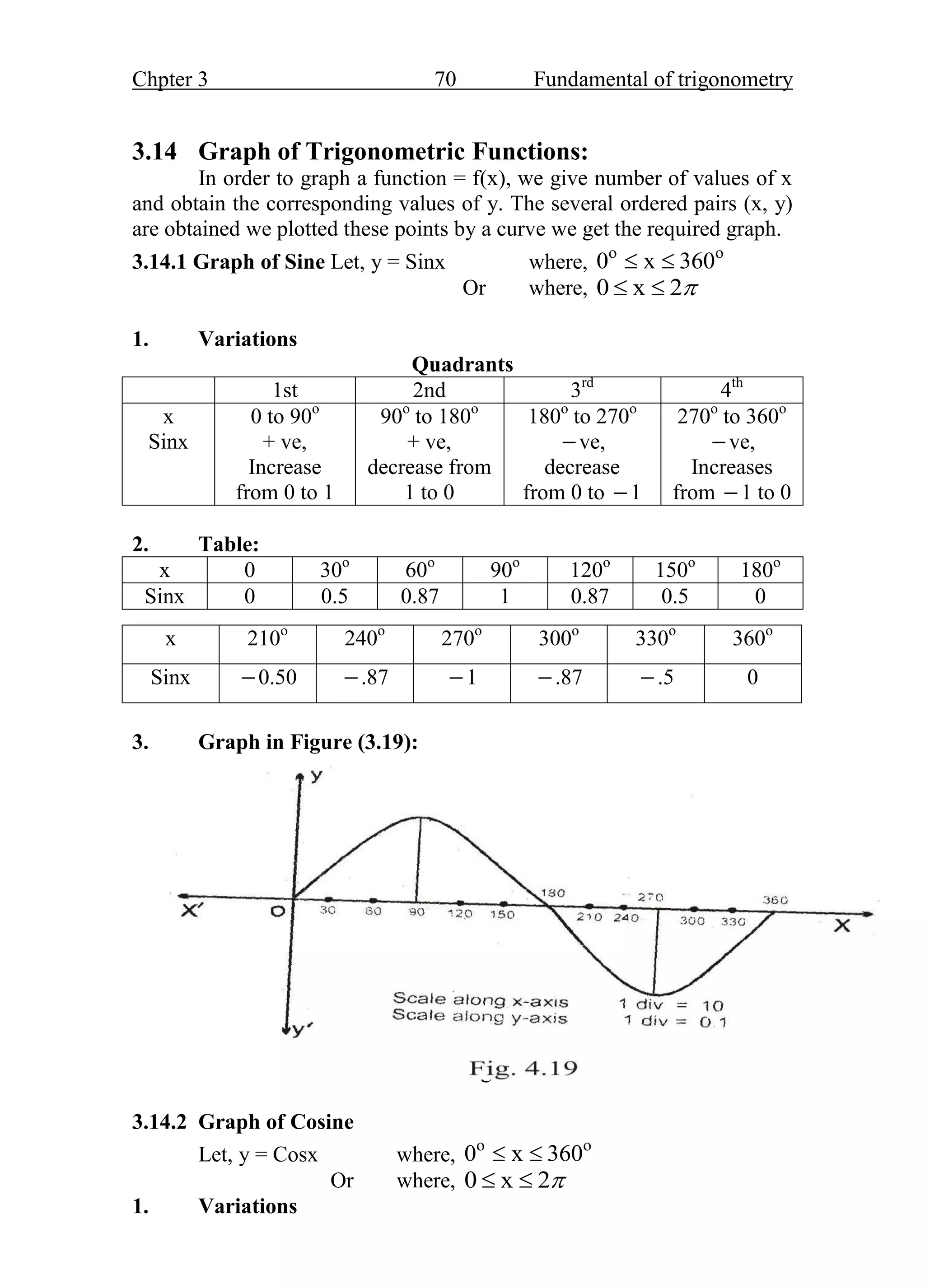
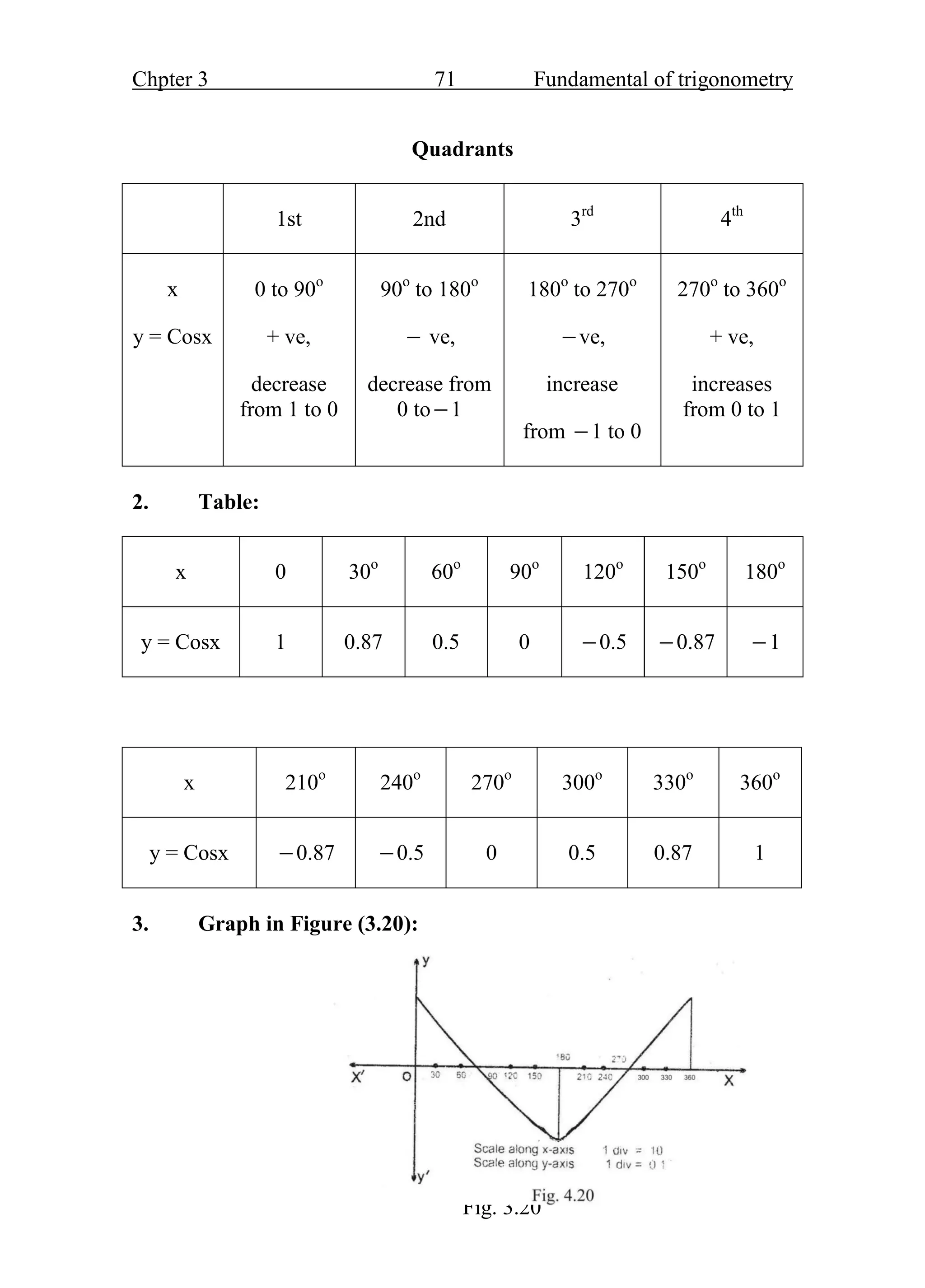
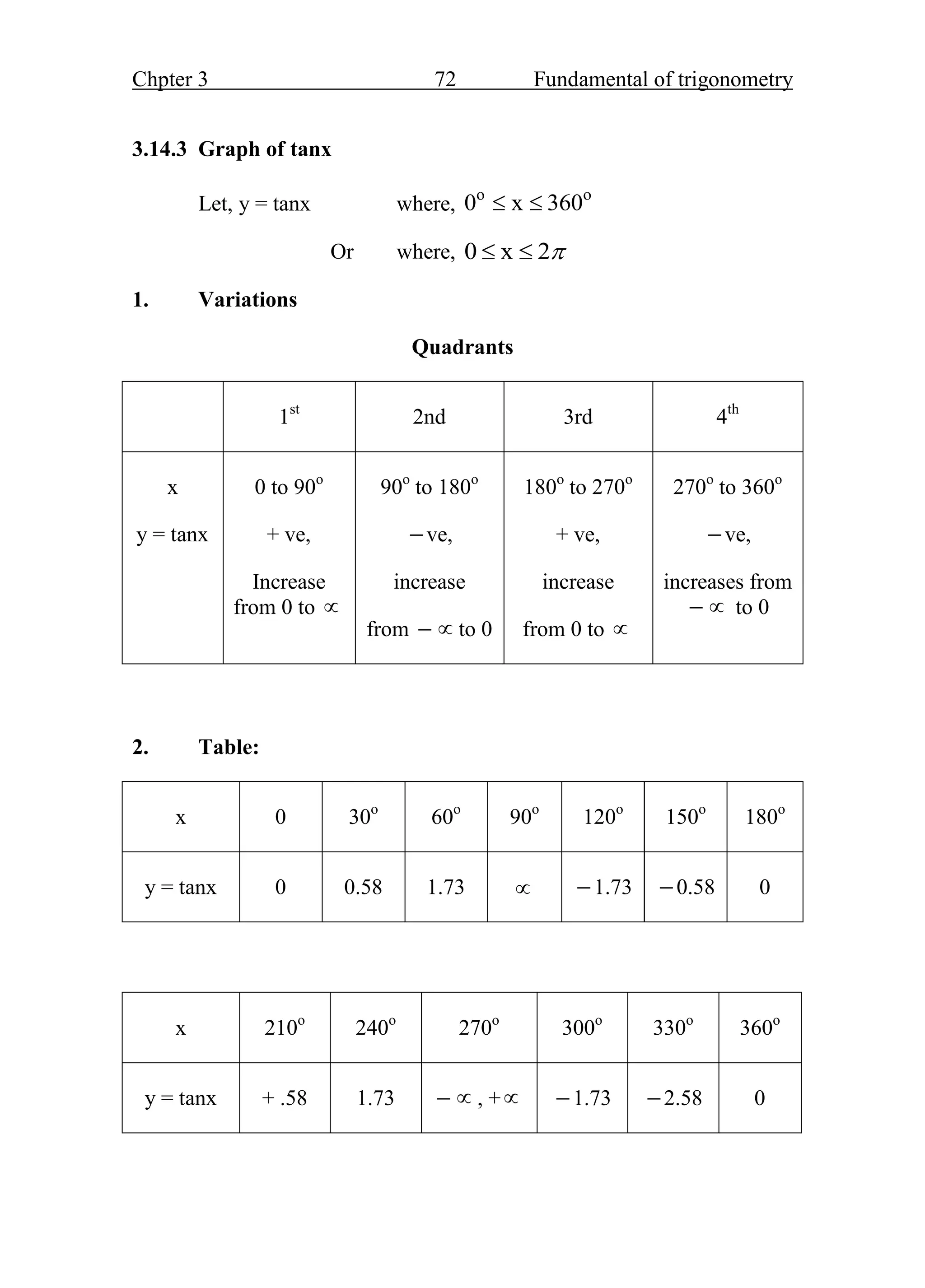
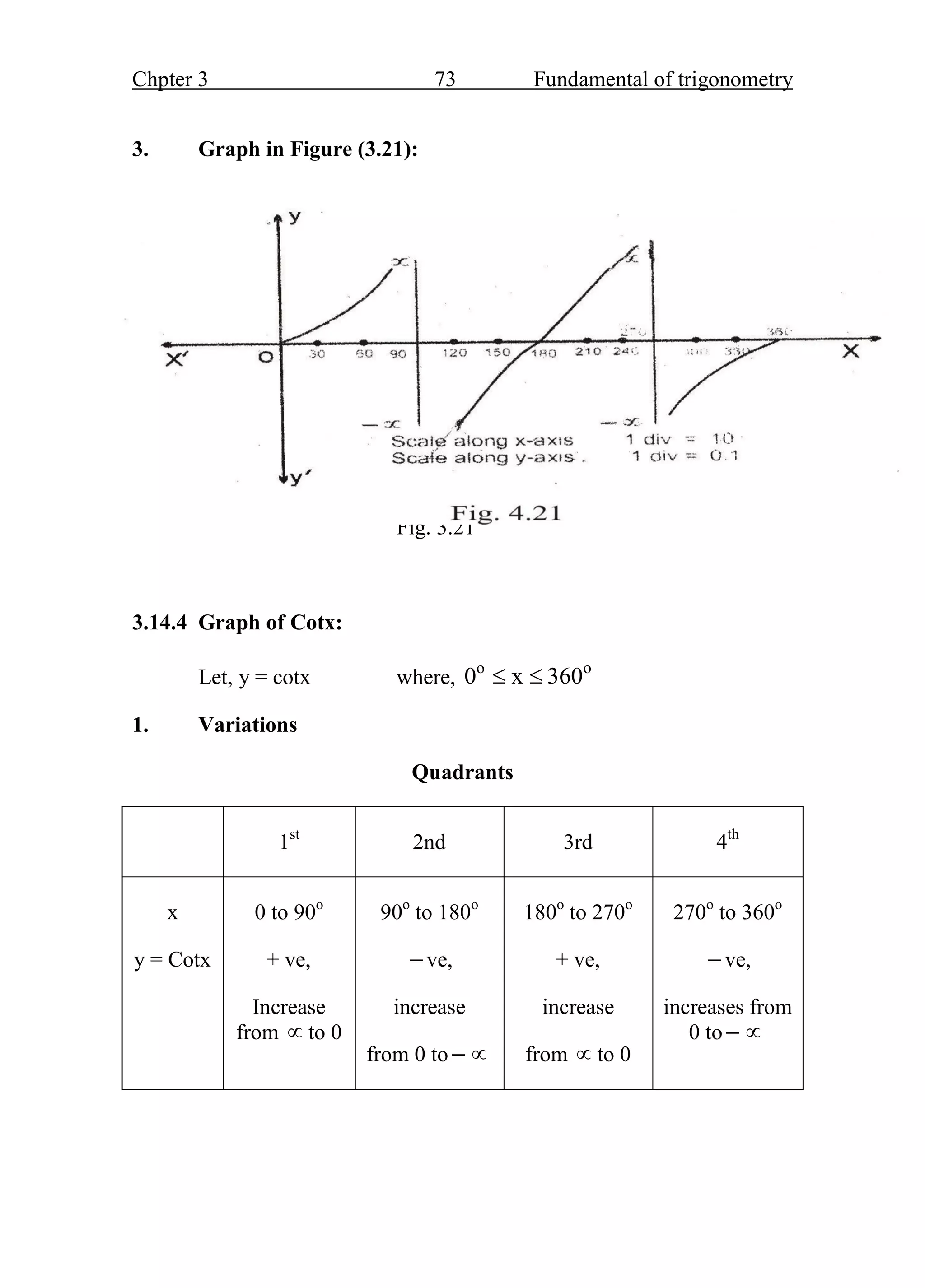
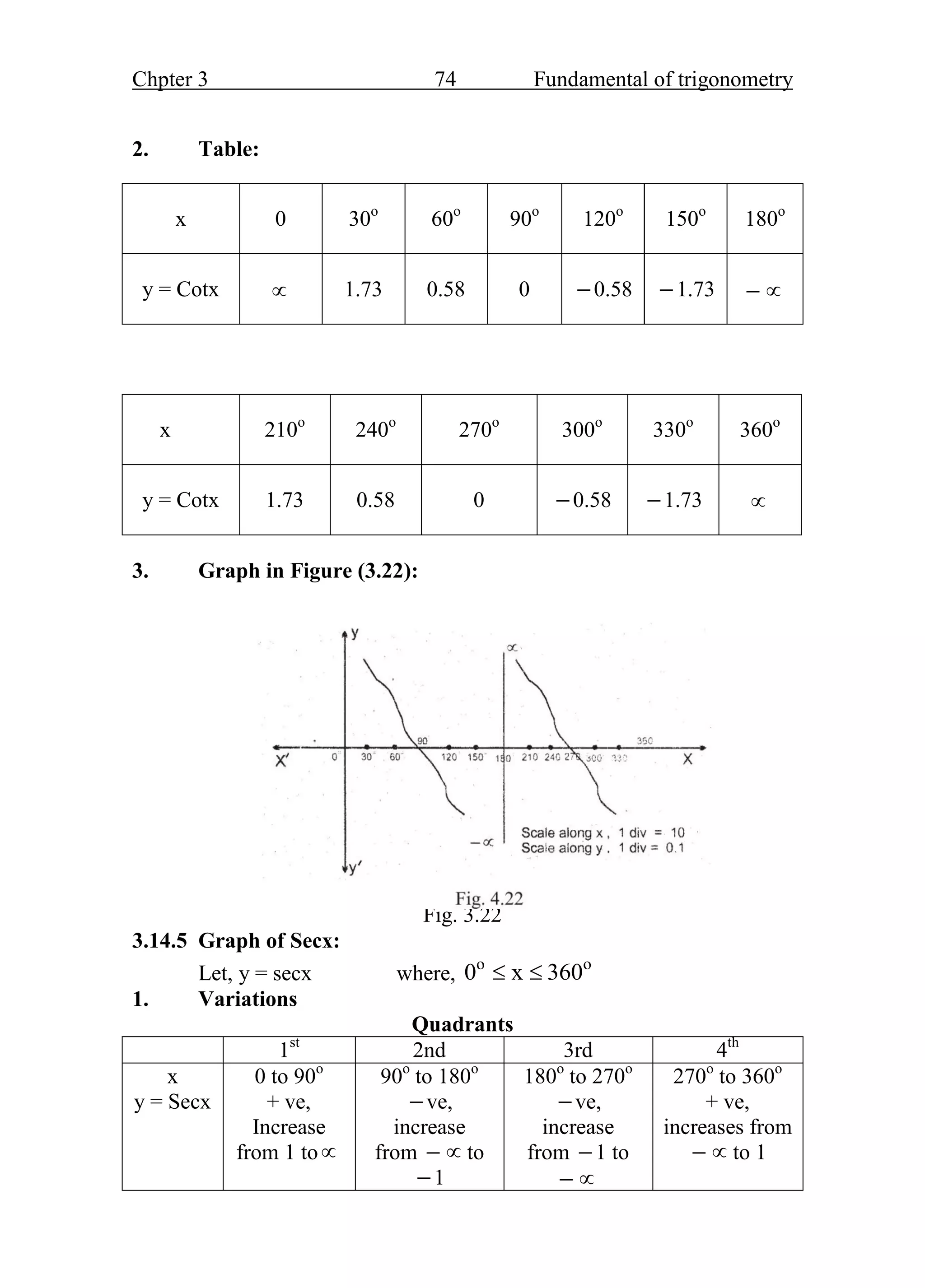
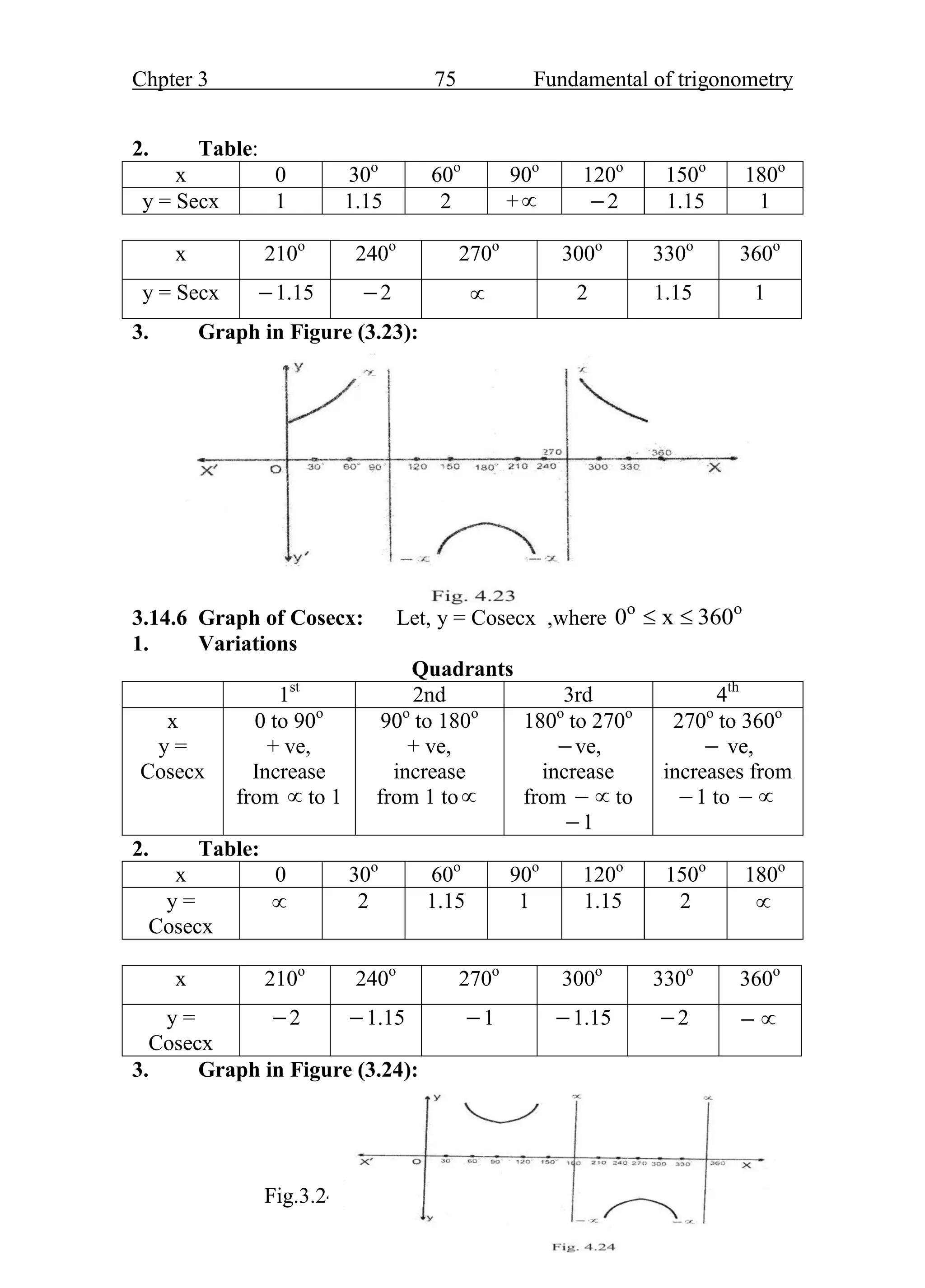
- The trigonometric ratios of sine, cosine, and tangent are defined based on the sides of a right triangle containing the angle of interest. These ratios are fundamental functions in trigonometry.