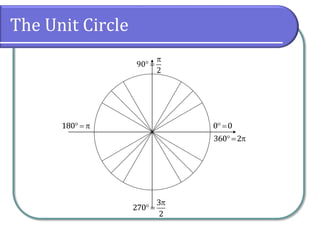
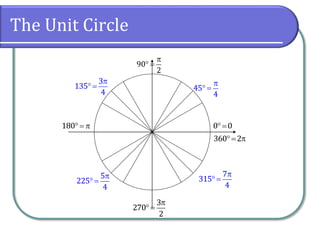
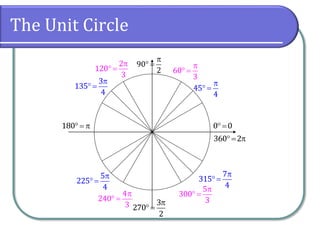
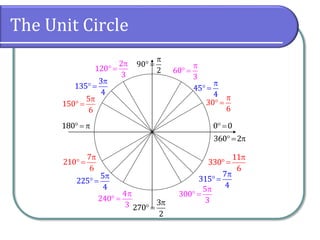
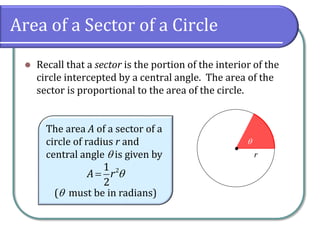
This document covers the concepts of radian measure in circular functions, including conversions between degrees and radians, and calculations for arc length and sector area. It provides formulas for determining arc lengths and sector areas based on central angles measured in radians. Additionally, it includes examples of applying these concepts practically, such as calculating distances using earth's radius.

1. 6.1 Radian Measure
Chapter 6 Circular Functions and Their Graphs

2. Concepts and Objectives
 Convert between degrees and radians
 Calculate the length of an arc intercepted by a given
angle
 Calculate the area of a sector

3. Radian Measure
 Up until now, we have measured angles in degrees.
Another unit of measure that mathematicians use is
called radian measure.
An angle with its vertex at
the center of a circle that
intercepts an arc on the
circle equal in length to the
radius of the circle has a
measure of 1 radian.
r
r
x
y

 = 1 radian

4. Radian Measure (cont.)
 You should recall that the circumference of a circle is
given by C = 2r, where r is the radius of the circle. An
angle of 360°, which corresponds to a complete circle,
intercepts an arc equal to the circumference.
 360 2 radians
 180 radians



180
1 radian

 1 radians
180
If no unit of angle measure is specified, then the
angle is understood to be measured in radians.

5. Radians and Degrees
 Converting between radians and degrees is just like
converting between any other type of units:
 Put the unit you are converting to on the top, and
the unit you are converting from on the bottom.
 Example: Convert 120° to radians.
120120°
180° 180
 2
3
= =
1
radians

6. Radians and Degrees (cont.)
 Example: Convert 57° 48' to radians
 Example: Convert radians to degrees
3
5

7. Radians and Degrees (cont.)
 Example: Convert 57° 48' to radians
 Example: Convert radians to degrees
3
5
 
  
57.8
180
    
48
57 48' 57 57.8
60


57.8
180
 0.321 1.01 radians

8. Radians and Degrees (cont.)
 Example: Convert 57° 48' to radians
 Example: Convert radians to degrees
3
5
 
  
57.8
180
    
48
57 48' 57 57.8
60


57.8
180
 0.321 1.01 radians
 
  
3 180
5
 3 36  108

9. The Unit Circle
0 0

 90
2
  180


3
270
2
  360 2

10. The Unit Circle
0 0

 45
4

 90
2

 
3
135
4
  180

 
5
225
4


3
270
2

 
7
315
4
  360 2

11. The Unit Circle
0 0

 45
4

 60
3

 90
2

 
2
120
3

 
3
135
4
  180

 
5
225
4

 
4
240
3 

3
270
2

 
5
300
3

 
7
315
4
  360 2

12. The Unit Circle
0 0

 30
6

 45
4

 60
3

 90
2

 
2
120
3

 
3
135
4

 
5
150
6
  180

 
7
210
6

 
5
225
4

 
4
240
3 

3
270
2

 
5
300
3

 
7
315
4


11
330
6
  360 2

13. Arc Length of a Circle
 The length of an arc is proportional to the measure of its
central angle.
•
r
s

The length s of the arc on
a circle of radius r created
by a central angle
measuring  is given by
( must be in radians)
s r

14. Arc Length of a Circle (cont.)
 Example: Find the length, to the nearest hundredth of a
foot, of the arc intercepted by the given central angle and
radius. 
 
5
1.38 ft,
6
r 

15. Arc Length of a Circle (cont.)
 Example: Find the length, to the nearest hundredth of a
foot, of the arc intercepted by the given central angle and
radius.
 Remember—the angle measure must be in radians. If
you are given an angle measure in degrees, you must
convert it into radians.

 
5
1.38 ft,
6
r 
 
 
  
 
5
1.38
6
s 3.61 ft

16. Arc Length of a Circle (cont.)
 Example: Find the length to the nearest tenth of a meter
of the arc intercepted by the given central angle and
radius.
  2.9 m, 68r 

17. Arc Length of a Circle (cont.)
 Example: Find the length to the nearest tenth of a meter
of the arc intercepted by the given central angle and
radius.
  2.9 m, 68r 
  
 
    
2.9 68
180
s
3.5 m

18. Using Latitudes
 Example: Erie, Pennsylvania is approximately due north
of Columbia, South Carolina. The latitude of Erie is
42° N, while that of Columbia is 34° N. If the Earth’s
radius is 6400 km, find the north-south distance
between the two cities.

19. Using Latitudes
 Example: Erie, Pennsylvania is approximately due north
of Columbia, South Carolina. The latitude of Erie is
42° N, while that of Columbia is 34° N. If the Earth’s
radius is 6400 km, find the north-south distance
between the two cities.
The measure of the central angle between Erie and
Columbia is 42° ‒ 34° = 8°. Therefore,
 6400 8 894 km
180
s
 
   
 

20. Area of a Sector of a Circle
 Recall that a sector is the portion of the interior of the
circle intercepted by a central angle. The area of the
sector is proportional to the area of the circle.
r

•
The area A of a sector of a
circle of radius r and
central angle  is given by
( must be in radians)
 21
2
A r 

21. Area of a Sector of a Circle
 Example: Find the area of a sector of a circle having the
given radius r and central angle  (round to the nearest
kilometer). 
 
2
59.8 km,
3
r 

22. Area of a Sector of a Circle
 Example: Find the area of a sector of a circle having the
given radius r and central angle  (round to the nearest
kilometer). 
 
2
59.8 km,
3
r 
   
  
 
21 2
59.8
2 3
A  2
3745 km

23. Classwork
 College Algebra
 Page 565: 26-52, page 539: 14-28, page 513: 74-80
(all evens)