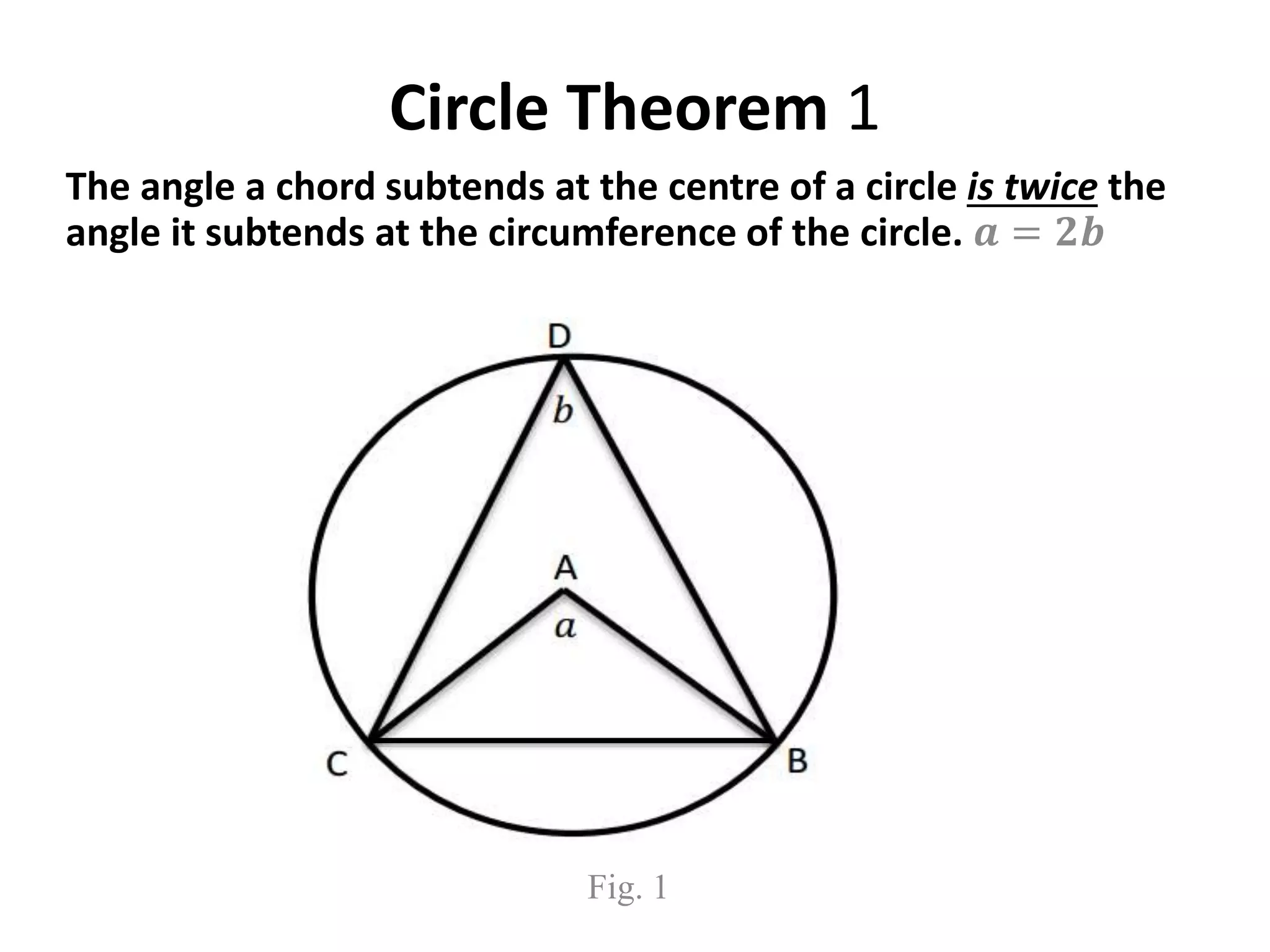
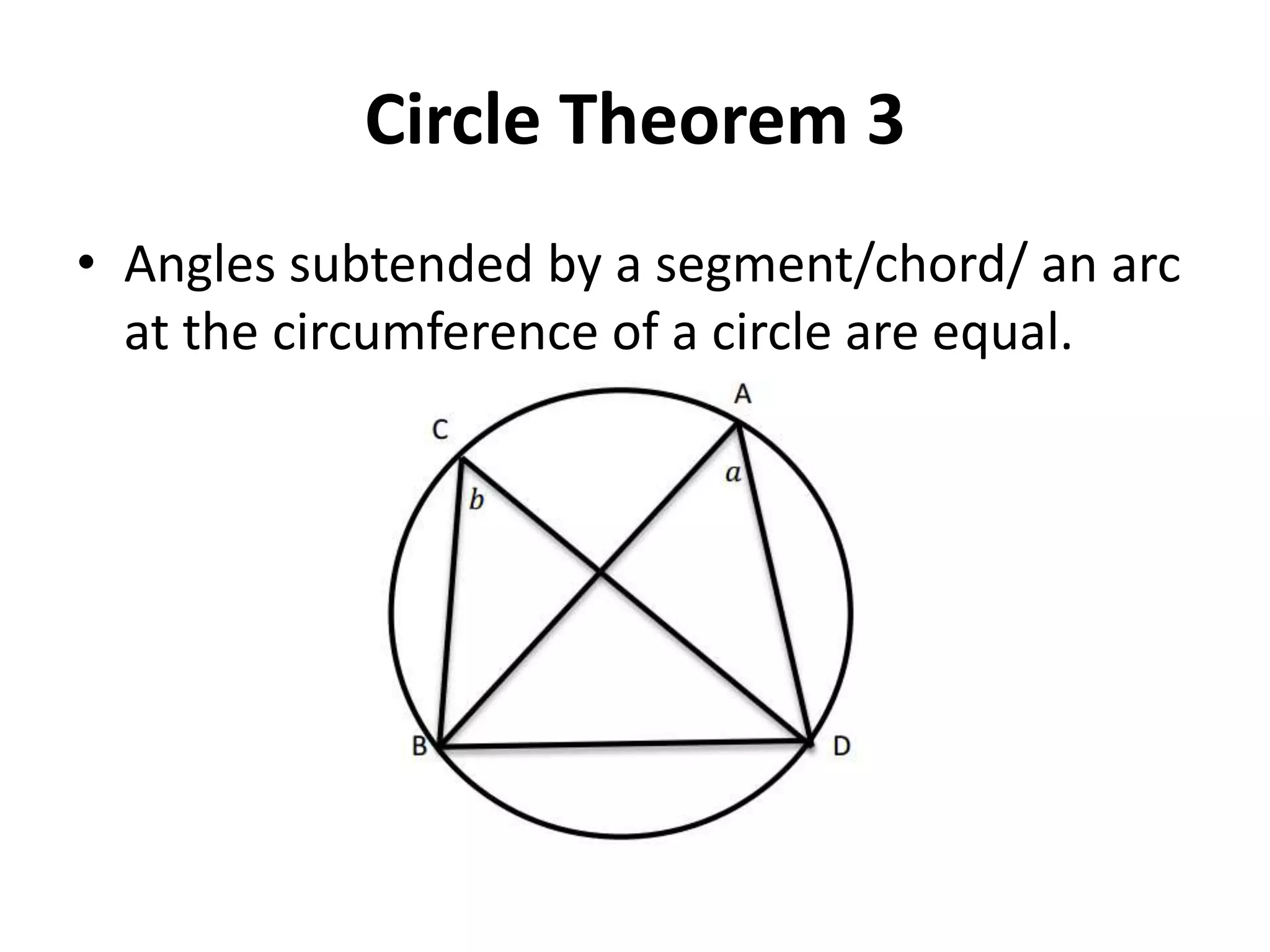
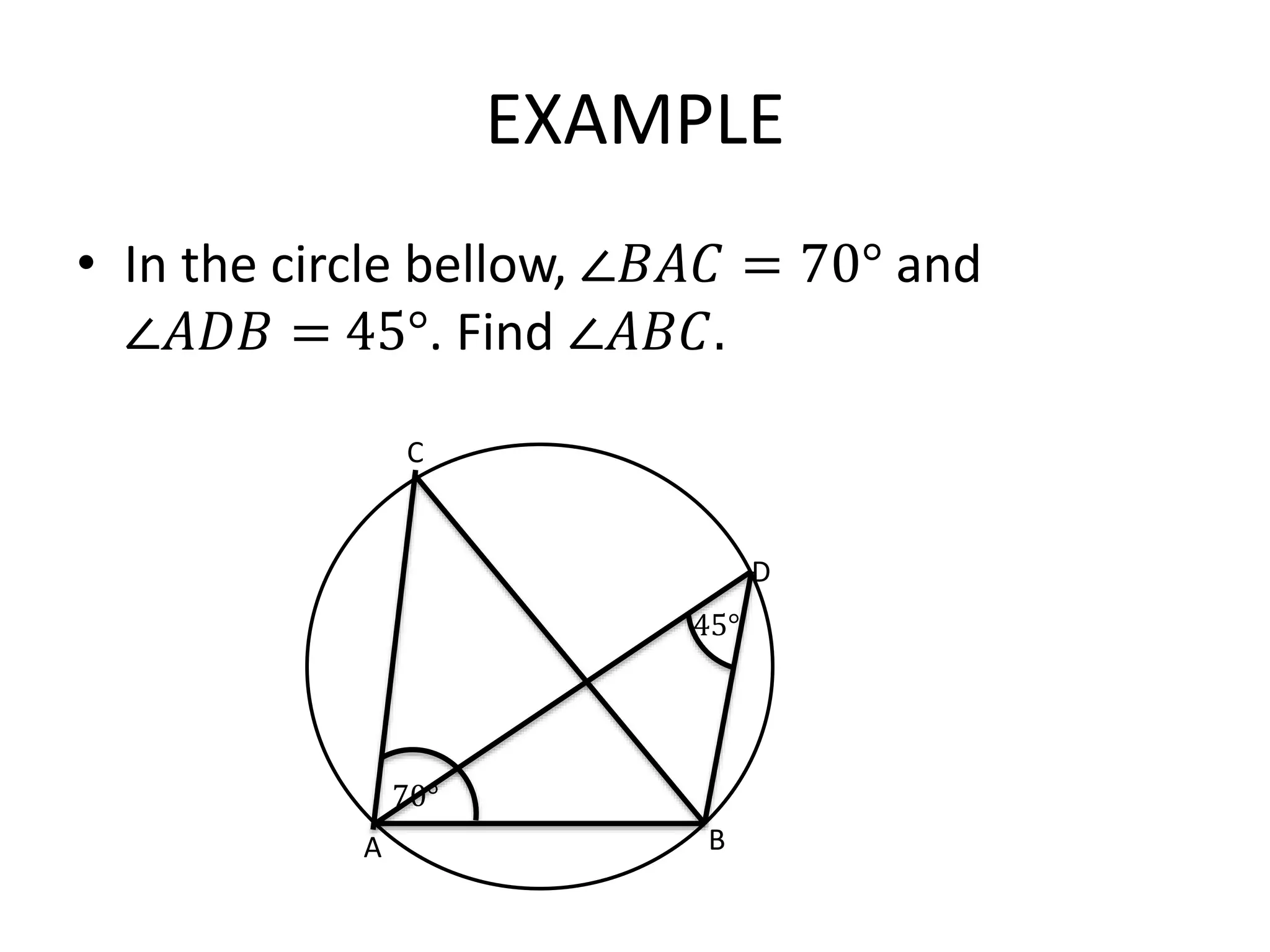
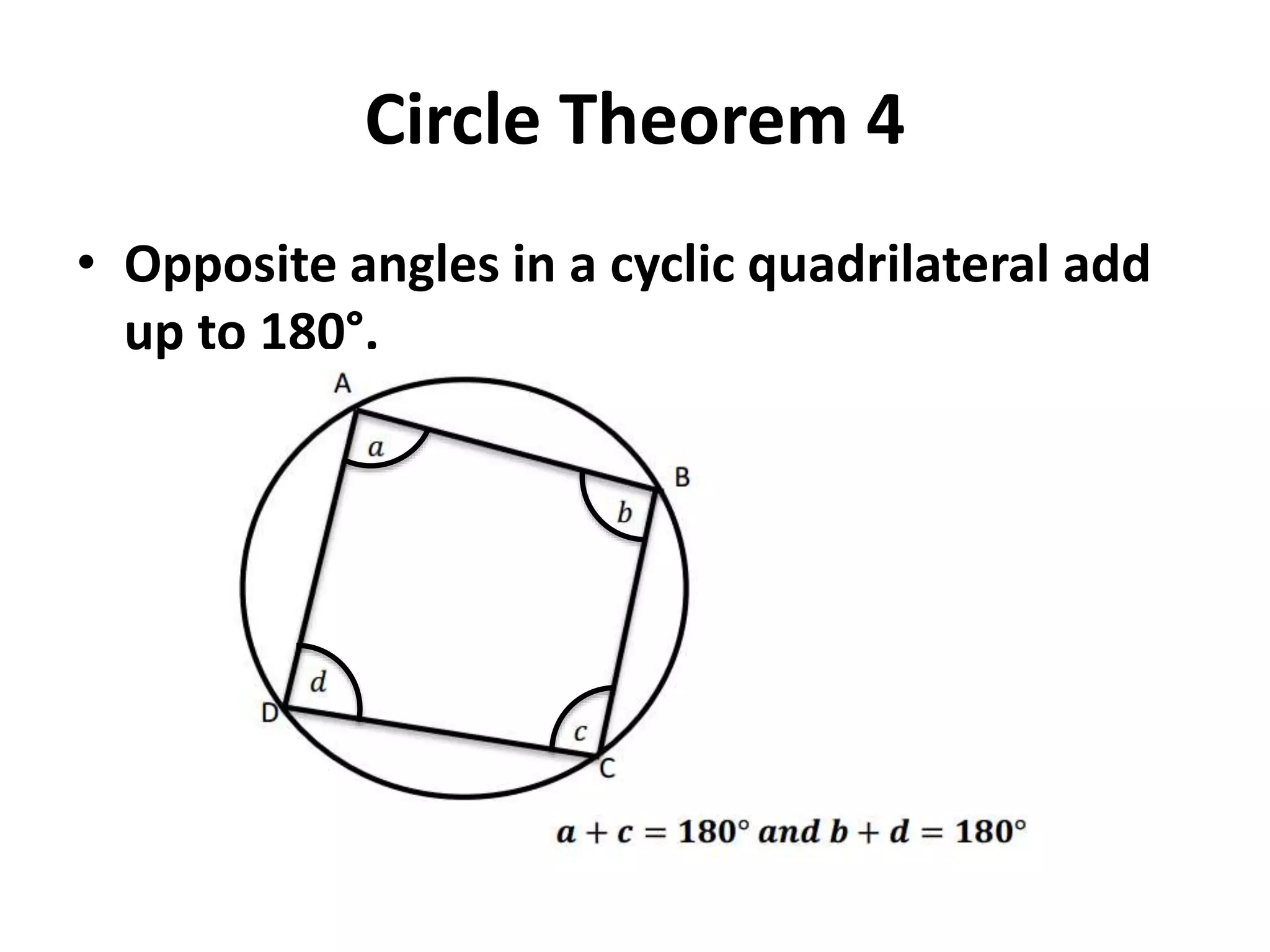
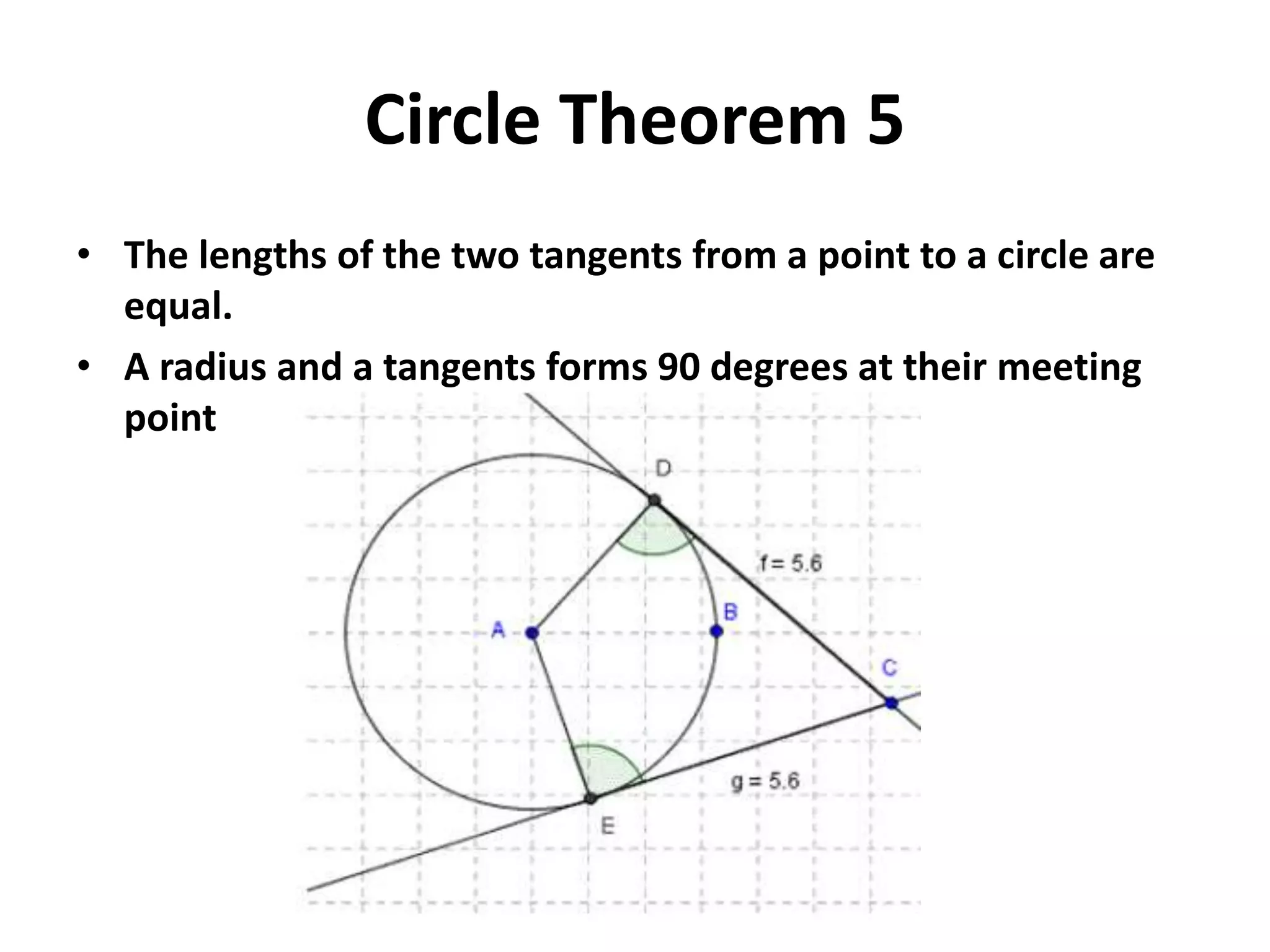
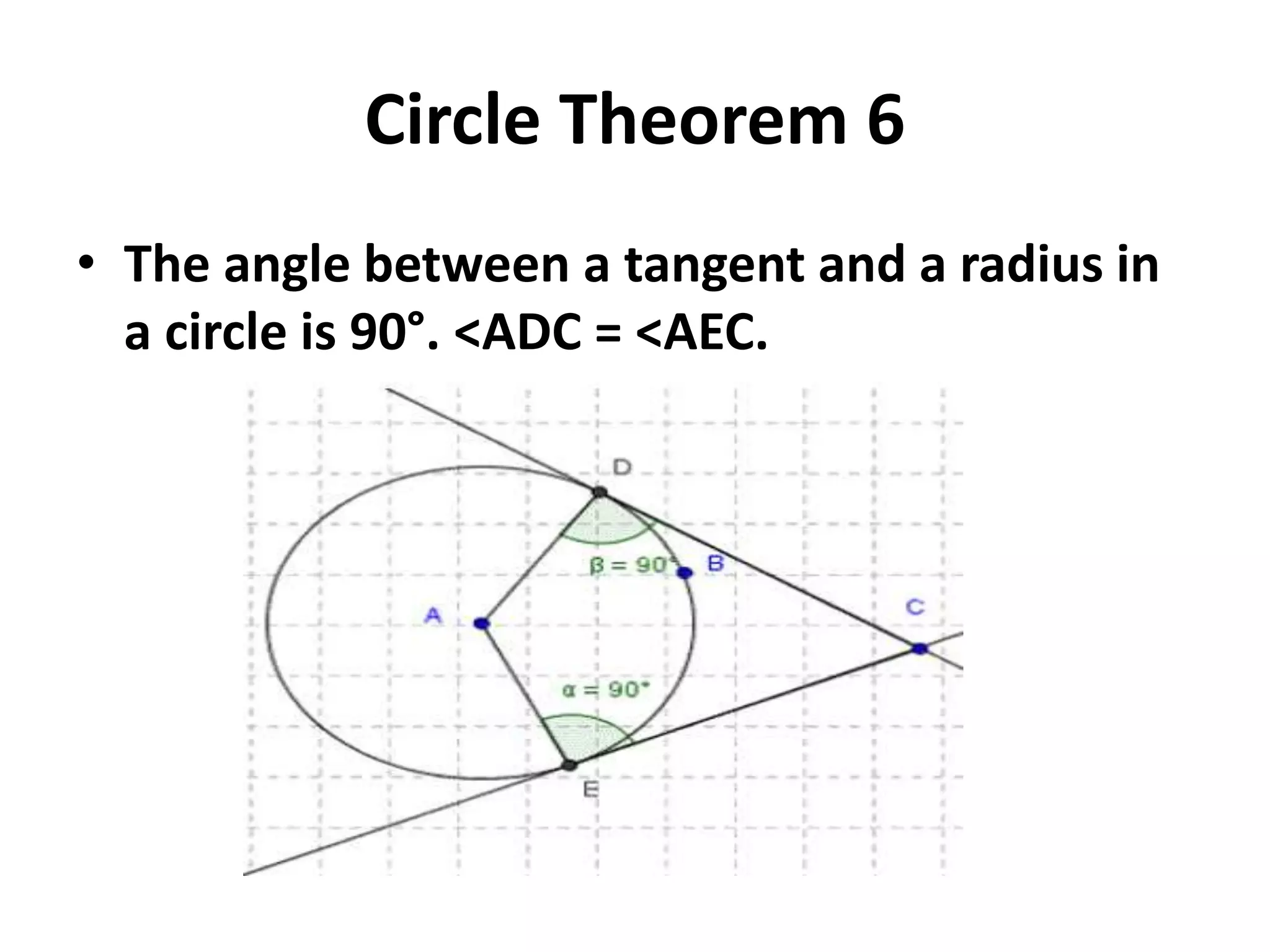
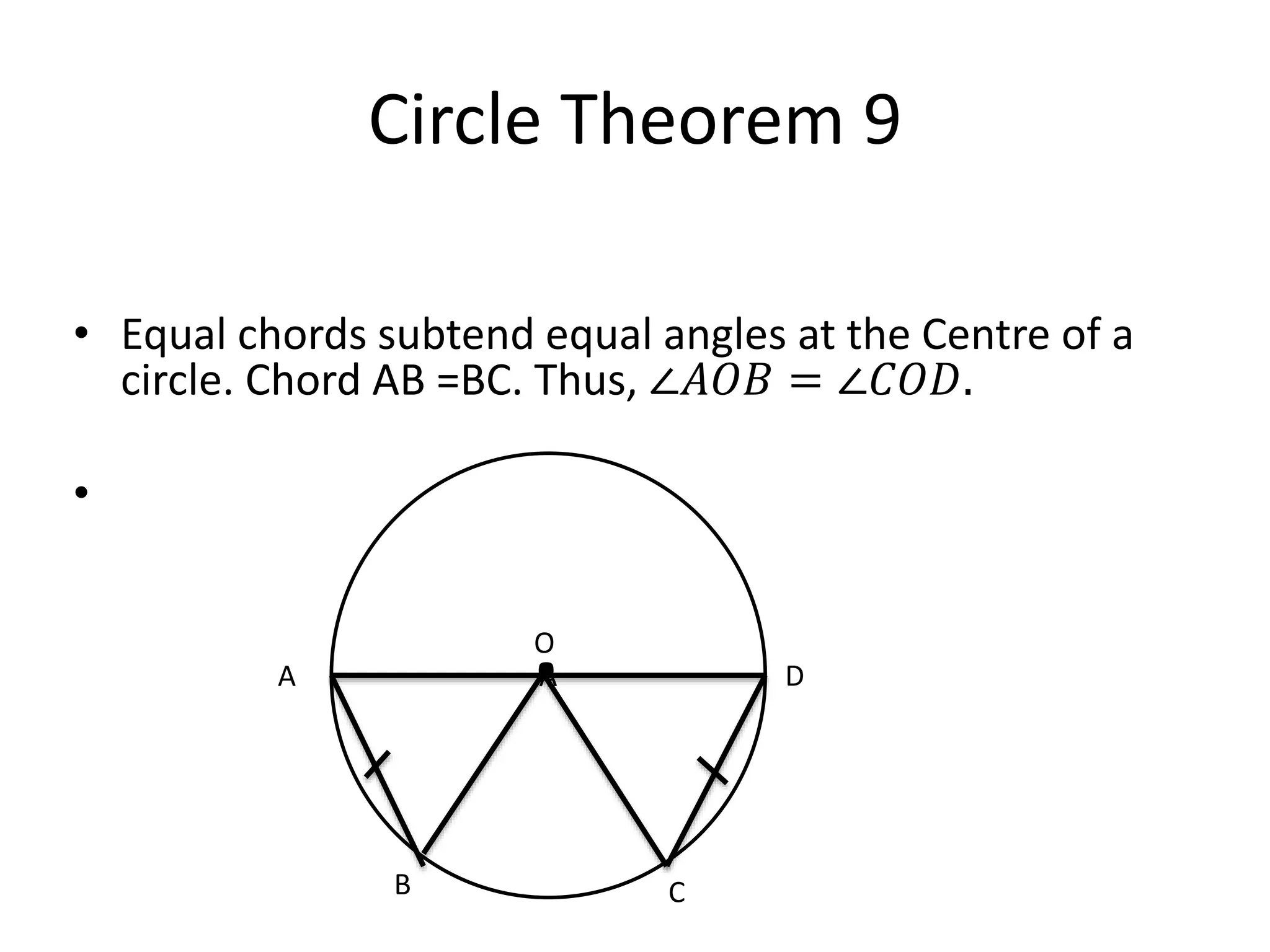
This document provides information on 10 circle theorems including: angles in a semicircle are right angles; opposite angles in a cyclic quadrilateral add up to 180 degrees; equal chords subtend equal angles; and tangents from a point are equal in length. Examples are worked through demonstrating each theorem. Real-life applications are discussed such as using circle theorems and Pythagoras' theorem to calculate distances on Earth and how circle geometry has remained important in theories of atoms and the universe.

1. THE CIRCLE THEOREM

2. INTRODUCTION
Revision on;
• the parts of a circle
• the sum of angles in polygons and
• the Pythagoras’ theorem.

3. PARTS OF A CIRCLE
• Here you are!

4. SUM OF INTERIOR ANGLES IN
POLYGONS
• We have learnt that the sum of angles in a
polygon can calculated by the formula
180°(𝑛 − 2), where 𝑛 is the number of sides
of the polygon. Now complete the table
below.
•
POLYGON No. of sides Sum of angles
Triangle 3 180°
Quadrilateral 4 360°
Pentagon
Hexagon
.
.
.

5. THE PYTHGORAS’ THEOREM
• Given the right-angled triangle ABC below,
𝐴
𝐵 𝐶
𝑨𝑪 𝟐 = 𝑨𝑩 𝟐 + 𝑩𝑪 𝟐.

6. THE CIRCLE THEOREMS
• 1 Angle at the centre
2 Angle in a semicircle
3 Angles in same segment
4 Cyclic quadrilateral
5 Tangent lengths
6 Tangent/radius angle
7 Alternate segment
8 Perpendicular
• 9 Equal chords

7. Circle Theorem 1
The angle a chord subtends at the centre of a circle is twice the
angle it subtends at the circumference of the circle. 𝒂 = 𝟐𝒃
Fig. 1

8. EXAMPLE
• In the diagram below, O is the centre of the
circle, |AO|=|BO| and ∠𝐴𝑂𝐵 = 68°. Find the
value of 𝑥.
O
A B
C
𝑥
68°

9. SOLUTION
∠AOB is twice x.
Thus, 𝑥 =
1
2
∠AOB
∴ 𝑥 =
1
2
(68°)
=34°

10. Circle Theorem 2
The angle the diametre of a circle subtends at the
circumference of the circle is 90°.

11. EXAMPLE
• 𝑂 is the centre of circle,
∆𝑃𝑄𝑅 is a triangle inscribed in the circle,
𝑃𝑂𝑅 is the diameter and ∠ 𝑅𝑃𝑄 = 55°. Find
∠ 𝑃𝑅𝑄.
P
Q
R
.
O
55°
P

12. SOLUTION
We know that ∠ 𝑃𝑄𝑅 = 90°
The sum of the interior angle of a triangle is 180°
⟹ ∠ 𝑃𝑅𝑄+ ∠ 𝑃𝑄𝑅+ ∠ 𝑄𝑃𝑅 = 180°
∠ 𝑃𝑅𝑄 = 180 – (∠ 𝑃𝑄𝑅+ ∠ 𝑄𝑃𝑅)
∠ 𝑃𝑅𝑄 = 180° − (90° + 55°)
= 35°

13. Circle Theorem 3
• Angles subtended by a segment/chord/ an arc
at the circumference of a circle are equal.

14. EXAMPLE
• In the circle bellow, ∠𝐵𝐴𝐶 = 70° and
∠𝐴𝐷𝐵 = 45°. Find ∠𝐴𝐵𝐶.
A B
D
C
45°
70°

15. SOLUTION
∠𝐴𝐶𝐵 = ∠𝐴𝐷𝐵 = 45°
The sum of the interior angle of a triangle is 180°
∴ ∠𝐴𝐶𝐵 = 180°-(45° + 70°)
= 85°

16. Circle Theorem 4
• Opposite angles in a cyclic quadrilateral add
up to 180°.

17. EXAMPLE
• Find the angles marked with letters in the
figure below.
A
C
D
D
95°
105°
𝑋
𝑌

18. SOLUTION
𝑋 + 105° = 180°
∴ 𝑋 = 180° − 105°
= 75°
𝑌 + 85° = 180°
∴ 𝑌 = 180° − 85°
= 95°

19. Circle Theorem 5
• The lengths of the two tangents from a point to a circle are
equal.
• A radius and a tangents forms 90 degrees at their meeting
point

20. EXAMPLE
O
𝑋
In the diagram below, 𝑂 is the centre
of the circle. Find ∠𝑋.
115°
A
B
C

21. SOLUTION
• ∠𝐴𝐵𝑂 = ∠𝐴𝐶𝑂 = 90°
• The sum of the interior angles of a
quadrilateral is 360°
• ∴ 𝑋 + 90° + 90°+ 115° = 360°
• ⟹ 𝑋 + 295° = 360°
• ⟹ 𝑋 = 360° − 295°
• = 65°

22. Circle Theorem 6
• The angle between a tangent and a radius in
a circle is 90°. <ADC = <AEC.

23. Circle Theorem 7
• Alternate segment theorem:
The angle (α) between the tangent and the
chord at the point of contact (D) is equal to
the angle (β) in the alternate segment*.

24. EXAMPLE
• In the diagram below, 𝑃𝑅 the diametre , 𝑃𝑇 is
the tangent. ∠𝑄𝑃𝑅 = 𝑎° and ∠𝑄𝑃𝑇 = 54°.
Find the value of 𝑎.
O
𝑎°
𝑃
𝑄
𝑅
𝑆
T
54°

25. SOLUTION
• ∠𝑃𝑄𝑅 = 90°
• Also ∠𝑃𝑅𝑄 = ∠𝑄𝑃𝑇 = 54°
⟹ 𝑎 + 54° + 90° = 180°
⟹ 𝑎 = 180° − 145°
⟹ 𝑎 = 35 °
(Theorem 2)

26. Circle Theorem 8
• Perpendicular from the centre bisects a
chord: 𝐶𝐸 = 𝐷𝐸
C
E
D
.

27. Circle Theorem 9
• Equal chords subtend equal angles at the Centre of a
circle. Chord AB =BC. Thus, ∠𝐴𝑂𝐵 = ∠𝐶𝑂𝐷.
•
• . . . .
Oao
B
A
O
C
A
B
. D

28. Circle Theorem 10
• Equal chords subtend equal angles at the
circumference of a circle. ∠𝐵𝐴𝑂 = ∠𝑂𝐷𝐶
A
B
O
D
C

29. PROOFS 9 AND 10
O
A
B
C F
E
D

30. SOLVED EXAMPLE
• In the diagram bellow, 𝑇𝐵 touched the circle
at B and 𝐵𝐷 is the diametre, ∠𝑇𝐵𝐴 = 31°.
Calculate
a. ∠𝐴𝐷𝐶
b. ∠𝐴𝐵𝐶
c. ∠𝐶𝐴𝐷
T
B
A
D
C
310
690

31. SOLUTION
• ∠𝐴𝐷𝐵 = ∠𝑇𝐵𝐴 =
• ∠𝐵𝐷𝐶 = ∠𝐵𝐴𝐶 =
a. ∠𝐴𝐷𝐶 = ∠𝐴𝐷𝐵 + ∠𝐵𝐷𝐶
=31°
+ 69°
=
b. ∠𝐴𝐶𝐵 = ∠𝐴𝐷𝐵 = ∠𝑇𝐵𝐴 =31°
From triangle 𝐴𝐵𝐶, ∠𝐴𝐵𝐶 =180° − 69° + 31° = 80°
c. ∠𝐵𝐴𝐷 =90°
∠𝐶AD = 90° − ∠𝐶AB = 90°- 69° = 21°
31°
69°
(Theorem 7)
(Theorem 3)
(Theorem 7)
100°

32. Real life Application of Circle Theorem
• Imagine you are standing on the surface of the
earth!

33. Real life Application of Circle Theorem
• You can use Pythagoras’ Theorem to calculate
the distance from the top of your head to the
Centre of the earth, the radius of the earth
and your height. Amazing, all by the
application of the Circle theorem!
• HERE YOU ARE!

34. Real life Application of Circle Theorem
• John Dalton reconstructed chemistry at the start of the 19th
century on the basis of atoms, which he regarded as tiny spheres,
and in the 20th century, models of circular orbits and spherical
shells were originally used to describe the motion of electrons
around the spherical nucleus. Thus circles and their geometry have
always remained at the heart of theories about the microscopic
world of atoms and theories about the cosmos and the universe.
• Geometry continues to play a central role in modern mathematics,
but its concepts, including many generalizations of circles, have
become increasingly abstract. For example, spheres in higher
dimensional space came to notice in 1965, when John Leech and
John Conway made a spectacular contribution to modern algebra
by studying an extremely close packing of spheres in 24-
dimensional space.