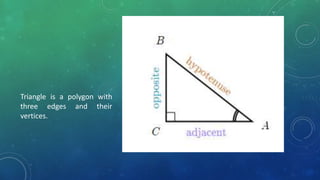
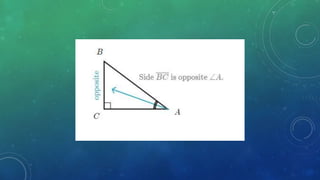
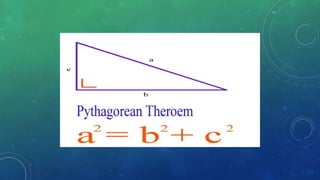
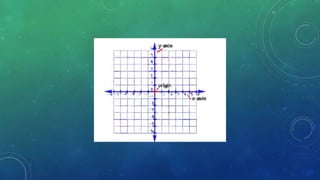
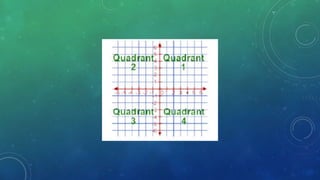
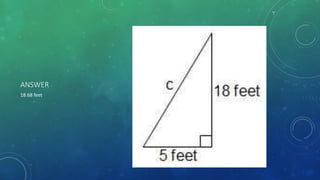
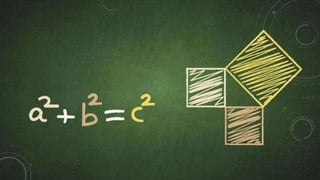This document provides an introduction to trigonometry. It discusses key topics like the Pythagorean theorem, coordinate plane, angles, degree and radian measurement, trigonometric functions, and trigonometric identities. The Pythagorean theorem states that the square of the hypotenuse is equal to the sum of the squares of the other two sides. Trigonometric functions are used to calculate values by plugging in angles. Trigonometric identities are equalities that are always true, unlike equations which are only true for certain values.

2. TRIGONOMETRY
12/01/17
RIPS-LAHORE
3RD SEMESTER
GROUP-A

3. CONTENTS
1. Introduction
2. The Pythagoras Theorem
3. The Coordinate Plane
4. The Angle
5. Degree and Radian
6. Trigonometric Functions
7. Trigonometric Identities
8. Sources

4. INTRODUCTION

5. • Trigonometry is derived from Greek word tri (meaning three), gon (meaning sides), and metron
(meaning measure).
• Trigonometry is a branch of mathematics that studies triangle and relationship between sides.

6. THE PYTHAGORAS THEOREM/ PYTHAGOREAN
THEOREM

7. The Triangle

8. Triangle is a polygon with
three edges and their
vertices.

12. The Pythagoras Theorem

13. • The PYTHAGORAS THEOREM states that the square of the hypotenuse is equal
to the sum of the square of other two sides.
𝑎2 + 𝑏2 = 𝑐2

15. THE COORDINATE PLANE

16. • It is formed by horizontal line called x-axis, and a vertical number line is called
the y-axis. These two axis intersect each other at a point is called origin.

18. The Four Quardrants

20. The Coordinate Plane And Trigonometry

22. THE ANGLE

23. • An angle is a measure of rotation we usually use the angle to measure the
amount by which a line has turned .

24. WHAT IS AN ANGLE?
Angle is the plane that can be generated by rotating a ray about its endpoint.

25. DIRECTIONS OF ANGLES
Angles are considered to be positive if generated anticlockwise
and negative if generated clockwise.

26. HOW TO MEASURE AN ANGLE
Angles can be measured in
• Degree
• Radian

27. THE DEGREE AND RADIAN

28. The Degree

29. DEFINITION
One degree is the measure of an angle generated by 1/360 of one revolution

30. CONVERSION
We use the following formula to convert degree into radian
1◦ = ∏ / 180 radian ≈ 0.01745 radian

31. The Radian

32. DEFINITION
In radian measure, angles are measured by the length of the arc that the angle subtends on a circle.
One unit of arc on a circle of radius 1 is called one radian.

33. CONVERSION
The following formula is used to convert radian into degrees.
1rad = ( 180/ ∏ )◦ ≈57.324 degree

34. TABLE OF CONVERSION FOR DEGREES AND RADIANS
DEGREES
30◦ 45◦ 60◦ 90◦ 180◦ 360◦
RADIAN ∏ ∕ 6 ∏ ∕ 4 ∏ ∕ 3 ∏ ∕ 2 ∏ 2∏

35. TRIGONOMETRIC FUNCTIONS

41. TRIGONOMETRIC IDENTITIES

42. Pythagorean Identities

43. • The Pythagorean trigonometric identity is a trigonometric identity expressing
the Pythagorean theorem in terms of trigonometric functions.

45. Three basic identities

46. 1) sin2θ + cos2θ =1
2) 1 + tan2θ = sec2θ
3) 1 + cot2θ = cosec2θ

48. Proof And Derivation

49. Examples

50. 1. sec2x + cosec2x = sec2x . cosec2x
2. secx ˗ (tanx . sinx) =
1
secx
3.
1+cosx
sinx
=
sinx
1 ˗ cosx
4. tanθ + cotθ = secθ . cosecθ

51. Find The Hypotenuse

52. ANSWER
18.68 feet

53. The Difference Between Trigonometric Identities And
Trigonometric Functions

54. Trigonometric Identities
• AN IDENTITY IS AN EQUALITY that is
true for any value of the
variable. (An equation is an equality
that is true only for certain values of
the variable.)
• sin2θ + cos2θ =1
Trigonometric Functions
• They are what are used to
CALCULATE values by plugging in x
or an angle theta.
• Trigonometric functions are sin, cos,
tan, csc, sec, cot 1/sin, 1/cos,
1/tan... etc

55. SOURCES

56. • Calculus - Howard Anton, Irl Bivens, 1Stephens Davis (10th Edition)
• Calculus And Its Applications – Larry J. Goldsteins, David C. Lay, David I.
Schneider, Nakhle H. Asmar (13th Edition)
• http://www.themathpage.com/atrig/trigonometric-identities.htm
• Image Courtesy: Google Images