This document discusses angles and trigonometry concepts including:
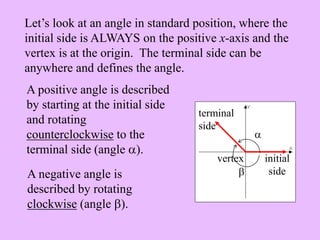
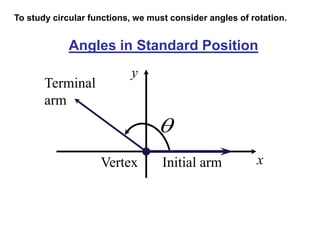
- Angles in standard position, which have their initial side on the positive x-axis and can have their terminal side in any of the four quadrants.
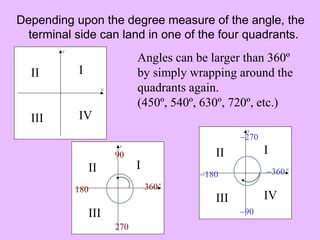
- Coterminal angles, which share the same terminal side but have different measures, obtained by adding or subtracting multiples of 360°.
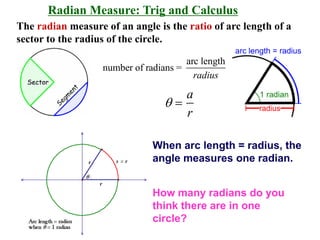
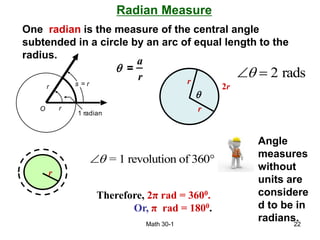
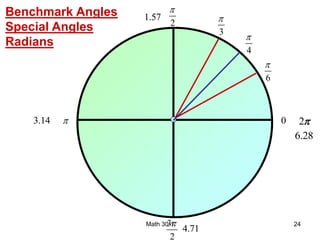
- Converting between degrees and radians, where one radian is the central angle subtended by an arc equal in length to the radius, and there are 2π radians in a full circle.