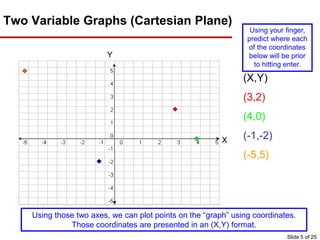
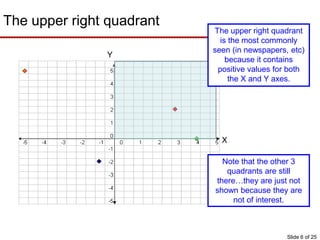
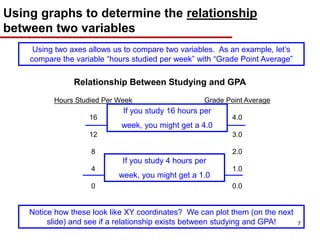
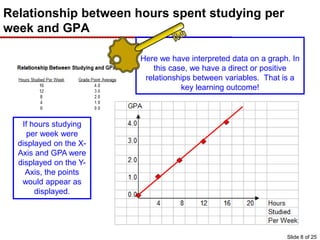
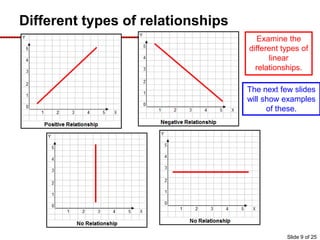
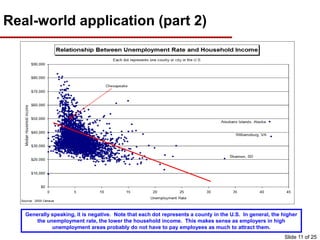
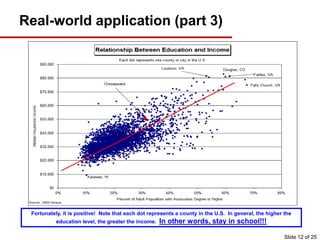
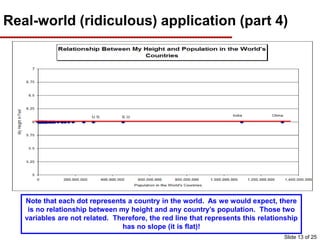
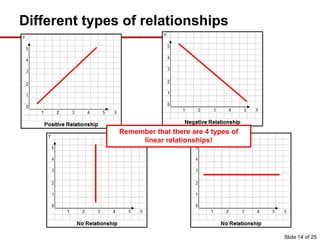
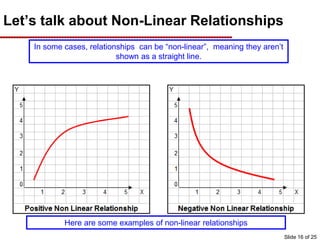
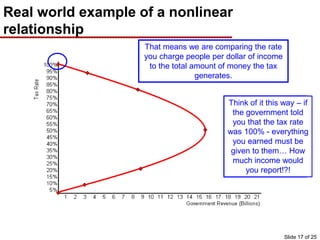
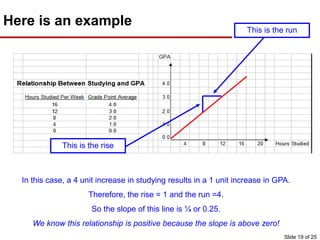
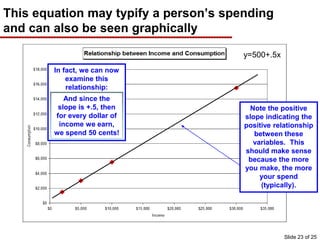
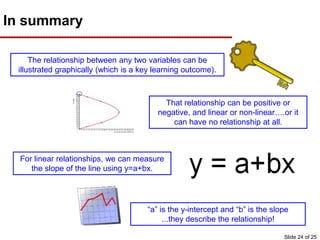
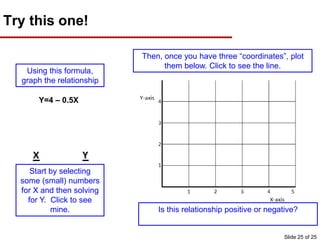
This document provides an overview of graphing principles and their application in economics. It begins with an introduction explaining the importance of understanding graphs. It then presents a series of slides explaining key graphing concepts like the Cartesian plane, linear relationships between variables, measuring slope, and using the equation y=mx+b to represent linear relationships algebraically. Examples are given for positive, negative, and no relationships between real-world variables like income and life expectancy. Non-linear relationships are also briefly discussed. The document emphasizes that understanding graphs is critical for success in economics courses.

1. The principles of graphing
Understanding the principles
of graphs and their meaning
are critical to understanding
economics.
The following material is designed to serve as a review on
graphing. You have probably seen all this material
before…many times. But it is important that you understand it
as we will rely extensively on graphs in this course.
If, after reviewing this material, you do not understand it, you
are strongly encouraged to seek my help or consult the
tutoring center!
Slide 1 of 25

2. Where are we headed?
We’ll cover this material starting from the
very beginning. Please bare with me.
Quickly, we’ll add details and
complexity and demonstrate concepts
in an economic framework.
It is critical that you understand this
material. You’ll see about 300 graphs
this semester and in each case, I’ll
assume you understand it.
Slide 2 of 25

3. Let’s start with the number line
Here is a number line.
Also note that only whole numbers are
shown. The number line is actually made up
of an infinite number of points each
representing some fraction of the line.
Note how the arrows signify that
numbers continue into infinity in both
directions.
Slide 3 of 25
½-3 ½

4. Two Variable Graphs (Cartesian Plane)
If we put two number lines together, then we get “space”. In this examples the
number lines are referred to as the X axis and the Y axis.
Slide 4 of 25

5. Two Variable Graphs (Cartesian Plane)
(X,Y)
(3,2)
(4,0)
(-1,-2)
(-5,5)
Using those two axes, we can plot points on the “graph” using coordinates.
Those coordinates are presented in an (X,Y) format.
Using your finger,
predict where each
of the coordinates
below will be prior
to hitting enter.
Y
X
Slide 5 of 25

6. Y
X
The upper right quadrant
The upper right quadrant
is the most commonly
seen (in newspapers, etc)
because it contains
positive values for both
the X and Y axes.
Note that the other 3
quadrants are still
there…they are just not
shown because they are
not of interest.
Slide 6 of 25

7. Relationship Between Studying and GPA
Hours Studied Per Week Grade Point Average
16 4.0
12 3.0
8 2.0
4 1.0
0 0.0
Using graphs to determine the relationship
between two variables
Using two axes allows us to compare two variables. As an example, let’s
compare the variable “hours studied per week” with “Grade Point Average”
Notice how these look like XY coordinates? We can plot them (on the next
slide) and see if a relationship exists between studying and GPA!
If you study 16 hours per
week, you might get a 4.0
If you study 4 hours per
week, you might get a 1.0
7

8. Relationship between hours spent studying per
week and GPA
If hours studying
per week were
displayed on the X-
Axis and GPA were
displayed on the Y-
Axis, the points
would appear as
displayed.
If those points were connected, then we’d
see an upward sloping line. This suggests a
POSITIVE RELATIONSHIP between studying
and GPA (in other words, the more you study,
the better your grades), which seems logical.
Here we have interpreted data on a graph. In
this case, we have a direct or positive
relationships between variables. That is a
key learning outcome!
Slide 8 of 25

9. Different types of relationships
Examine the
different types of
linear
relationships.
The next few slides
will show examples
of these.
Slide 9 of 25

10. Let’s practice! Try to identify these real-
world linear relationship
What do you think the relationship between income and life
expectancy is?
Positive, negative, or no relationship?
Generally speaking, it is positive. Note that each dot represents a country. In general, the higher the
income, the higher the life expectancy. This can be seen by placing a line (in red) over the dots.
This may not seem fair, but it is true. People living in countries with higher incomes usually have better
access to doctors and dentists and usually have access to a broader array of foods.
Slide 10 of 25

11. What is the relationship between the unemployment rate
and income?
Positive, negative, or no relationship?
Real-world application (part 2)
Generally speaking, it is negative. Note that each dot represents a county in the U.S. In general, the higher
the unemployment rate, the lower the household income. This makes sense as employers in high
unemployment areas probably do not have to pay employees as much to attract them.
Slide 11 of 25

12. Real-world application (part 3)
What is the relationship between education and
income?
Positive, negative, or no relationship?
Fortunately, it is positive! Note that each dot represents a county in the U.S. In general, the higher the
education level, the greater the income. In other words, stay in school!!!
Slide 12 of 25

13. Real-world (ridiculous) application (part 4)
What is the relationship between my height (6 feet) and population in
the world’s countries?
Positive, negative, or no relationship?
Note that each dot represents a country in the world. As we would expect, there
is no relationship between my height and any country’s population. Those two
variables are not related. Therefore, the red line that represents this relationship
has no slope (it is flat)!
Slide 13 of 25

14. Different types of relationships
Remember that there are 4 types of
linear relationships!
Slide 14 of 25

15. Give it a shot!
• Determine two variables that could be
measured.
– Examples include income, hours worked, wealth,
education, population or many others.
– Variables can also include non-economic
measures such as speed, distance, strength, time
spent playing video games or many others.
• Then determine what you think the relationship
between those two variables would be.
– Appropriate answers will be either positive (also
called direct), negative (also called inverse) or no
relationship.
• Continue this exercise until you have uncovered
a positive and negative relationship and no
relationship.
If you want, you can
submit these to me via
email (slacroix@tcc.edu)
and I’ll let you know if you
are on the right track!
Slide 15 of 25

16. Let’s talk about Non-Linear Relationships
Here are some examples of non-linear relationships
In some cases, relationships can be “non-linear”, meaning they aren’t
shown as a straight line.
Slide 16 of 25

17. Real world example of a nonlinear
relationship
Imagine we are comparing tax rates to
tax revenue.
That means we are comparing the rate
you charge people per dollar of income
to the total amount of money the tax
generates.
I think you’d agree
that in general,
higher tax rates
result in higher tax
revenue.
That would be true
up to a point. At
some point, as rates
get higher, we might
expect people to stop
working or maybe
they’d hide their
income.
This idea is referred to
as the “Laffer Curve”.
It is used to illustrate
the idea that the
government can
maximize revenues by
setting tax rates at
some optimal point.
Think of it this way – if
the government told
you that the tax rate
was 100% - everything
you earned must be
given to them… How
much income would
you report!?!
Slide 17 of 25

18. Let’s turn our attention to
measuring the slope of a line
The slope of a line can be measured using this formula:
Or
Slide 18 of 25

19. Here is an example
In this case, a 4 unit increase in studying results in a 1 unit increase in GPA.
Therefore, the rise = 1 and the run =4.
So the slope of this line is ¼ or 0.25.
We know this relationship is positive because the slope is above zero!
This is the rise
This is the run
Slide 19 of 25

20. Example of calculating slope (part 2)
In this case, a 4 unit increase in beer consumption results in a 1 unit decrease in GPA.
Therefore, the rise = -1 and the run =4.
Therefore the slope of this line is -¼ or -0.25
We know this relationship is negative because the slope is below zero!
Slide 20 of 25

21. Equation of linear relationship
y = a+bx
Where y= Dependent variable
a=vertical (y-axis) intercept
B=slope
x= Independent variable
Any linear relationship can be summarized using the following formula:
You may have learned this as “Y=mX+b”. If you
understand that..that is fine. We use this
formula because it is used in the textbook
Slide 21 of 25

22. Let’s take a look at that formula
Suppose we have the equation:
y=500+.5x
Then we can plug in values for x to get y
This (500) is “a”
which is also
called the “Y-
intercept”
This (+.5) is
“b” which is
also called the
“slope”
So if you pick a number
at random (say $2000)
and plug it into X, you
get
Y= 500+(.5*2000)…
which equals $1500
22

23. This equation may typify a person’s spending
and can also be seen graphically
Note the positive
slope indicating the
positive relationship
between these
variables. This
should make sense
because the more
you make, the more
your spend
(typically).
In fact, we can now
examine this
relationship:
Since the Y-Intercept
is $500 we know that
even if you do not
earn any income,
you’ll spend $500.
And since the
slope is +.5, then
for every dollar of
income we earn,
we spend 50 cents!
y=500+.5x
Slide 23 of 25

24. In summary
The relationship between any two variables can be
illustrated graphically (which is a key learning outcome).
That relationship can be positive or
negative, and linear or non-linear….or it
can have no relationship at all.
For linear relationships, we can measure
the slope of the line using y=a+bx.
“a” is the y-intercept and “b” is the slope
...they describe the relationship!
Slide 24 of 25

25. It’s negative.
For each 1 unit increase in X, Y falls by 0.5!
Try this one!
Y=4 – 0.5X
Using this formula,
graph the relationship
Start by selecting
some (small) numbers
for X and then solving
for Y. Click to see
mine.
Then, once you have three “coordinates”, plot
them below. Click to see the line.
Is this relationship positive or negative?
Slide 25 of 25