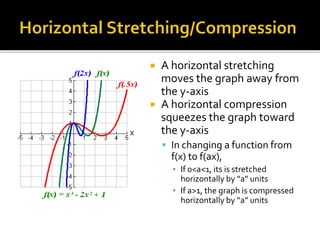
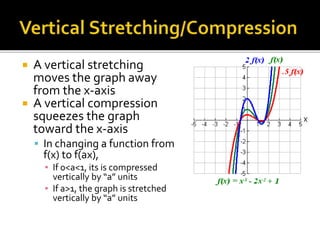
The document discusses function transformations including shifts, reflections, and stretches/compressions. It defines these transformations and provides examples of how they affect the graph of a function. Specifically, it explains that a shift moves a graph up/down or left/right along an axis, a reflection flips the graph across an axis, and a stretch or compression changes the scale of the graph along an axis. Examples are given of reflecting across the x-axis or y-axis and horizontally or vertically stretching/compressing a function. In the end, students are asked to write equations for specific transformations of a quadratic function.

1. By: Ms. Ball

2.  Take a moment and quietly discuss with a
neighbor, what are some parent functions
that you remember from earlier in this unit?
 Do you recall the nameAND the equation?

4.  Now that we remember some of our parent
functions, we can start to manipulate, or
transform them!
 Before we start, can you guess what a
transformation is?
 Think about different things that transform in the
world… what usually happens?

5.  Definition:
 The graph of a function is transformed when its
parent function is changed.
 There are three (3) types of transformations:
1. Shifts
2. Reflections
3. Stretches and Compressions

6.  Definition:
 When a graph is shifted it moves either up, down,
left, or right.
 Think about the x-y coordinate plane.Which
axis goes from left to right?What about up
and down?

7.  When an image is reflected, it is flipped like a
mirror
 There are 2 main reflections:
 About (across) the x-axis
 About the y-axis
 What type of reflection
is pictured here?

8.  The coefficients of a function determine how
much it is stretched or compressed
 Given y = f(x),
 Horizontal stretching/compression will give you
y = f(ax), where “a” is a constant
 Vertical stretching/compression will give you
y = a f(x), again “a” is a constant

9.  A horizontal stretching
moves the graph away from
the y-axis
 A horizontal compression
squeezes the graph toward
the y-axis
 In changing a function from
f(x) to f(ax),
▪ If 0<a<1, its is stretched
horizontally by “a” units
▪ If a>1, the graph is compressed
horizontally by “a” units

10.  A vertical stretching
moves the graph away
from the x-axis
 A vertical compression
squeezes the graph
toward the x-axis
 In changing a function from
f(x) to f(ax),
▪ If 0<a<1, its is compressed
vertically by “a” units
▪ If a>1, the graph is stretched
vertically by “a” units

11.  Here’s a short video to go over what we just learned…
https://www.youtube.com/watch?v=7S5HF38DnUY

12.  Using the quadratic as your parent function,
write the equations of the given
transformations:
 Shifted 5 units up
 Shifted 3 units left, and stretched horizontally by
2
 Reflected across the y-axis, and shifted up 4