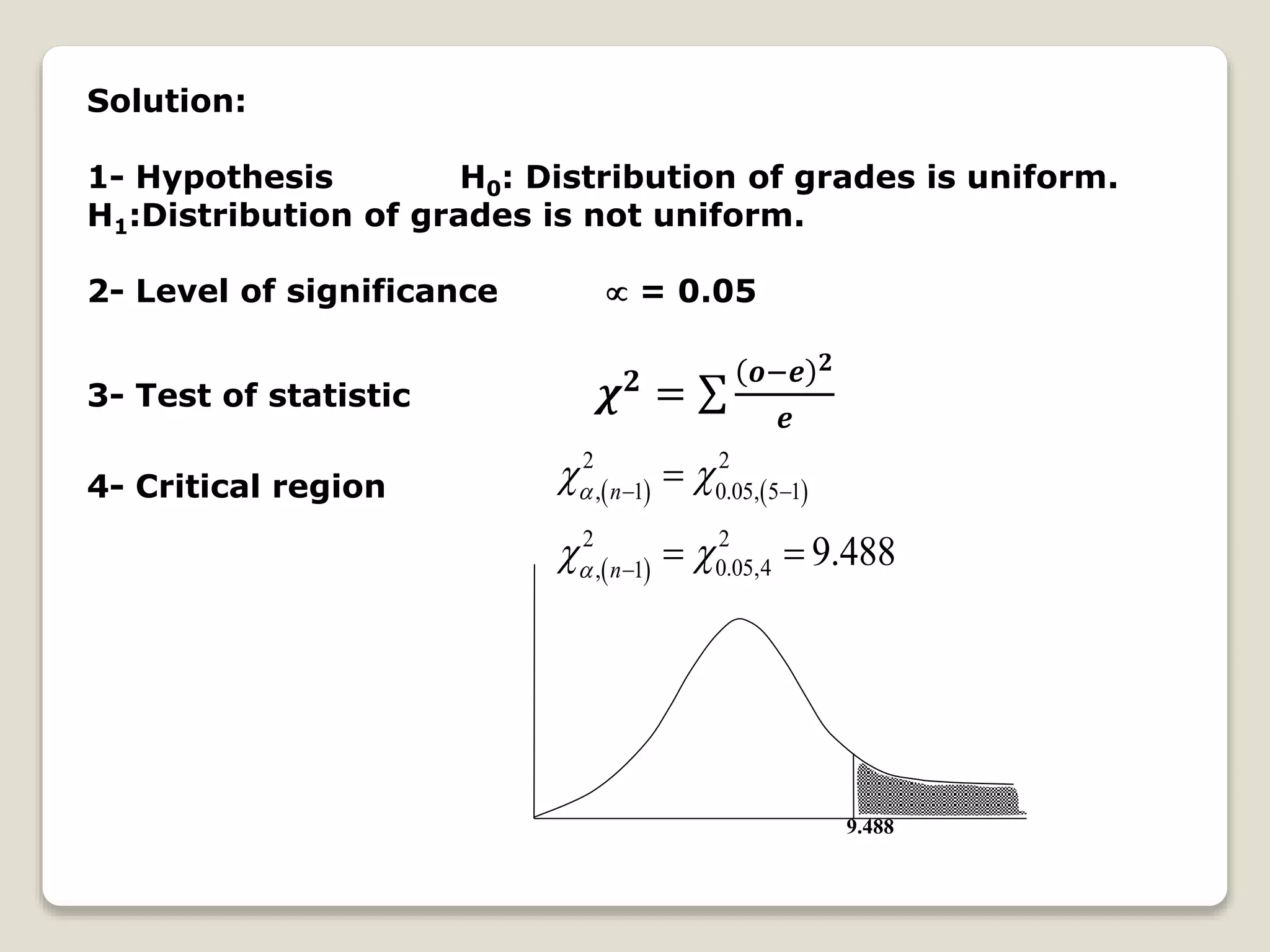
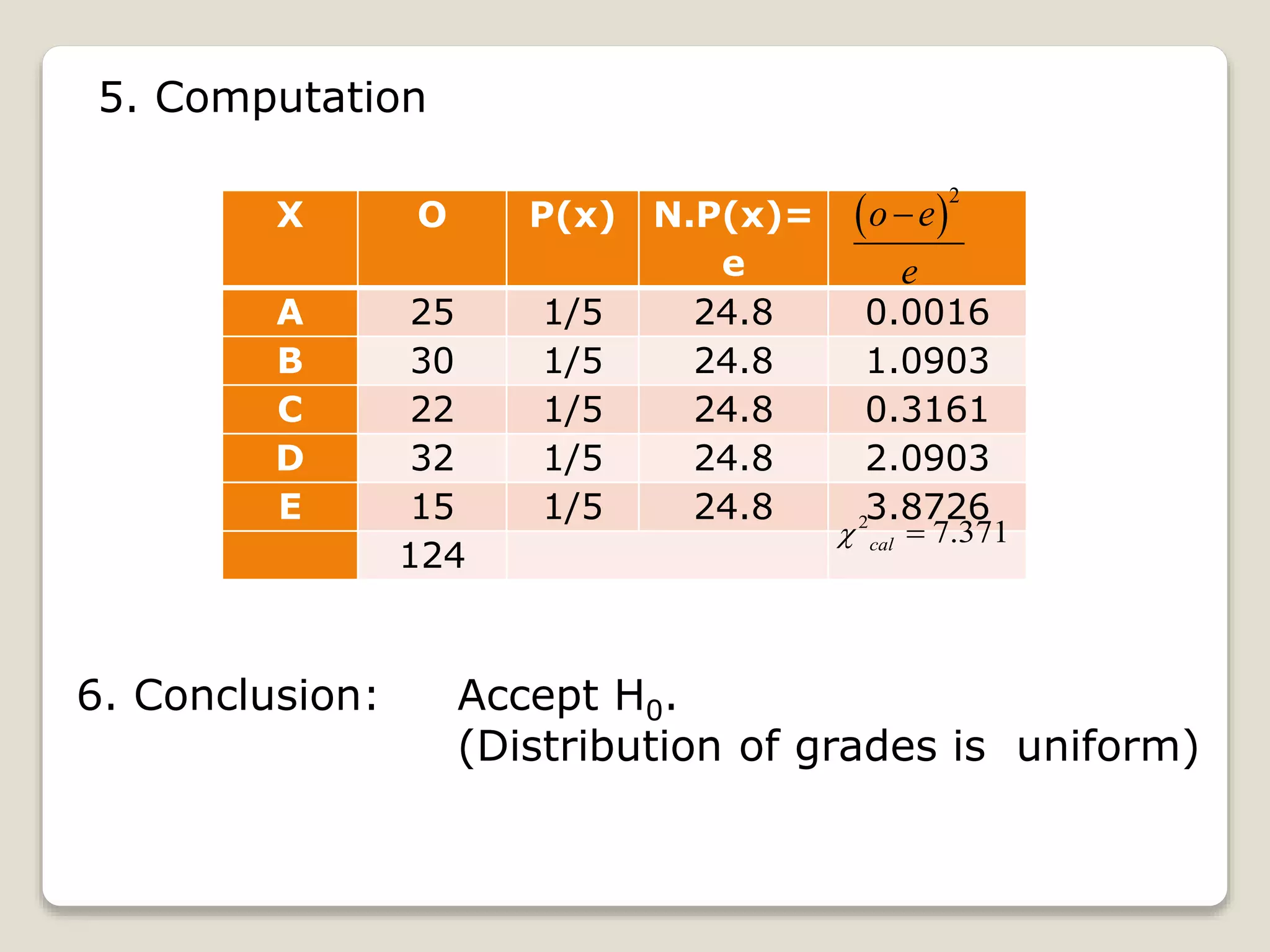
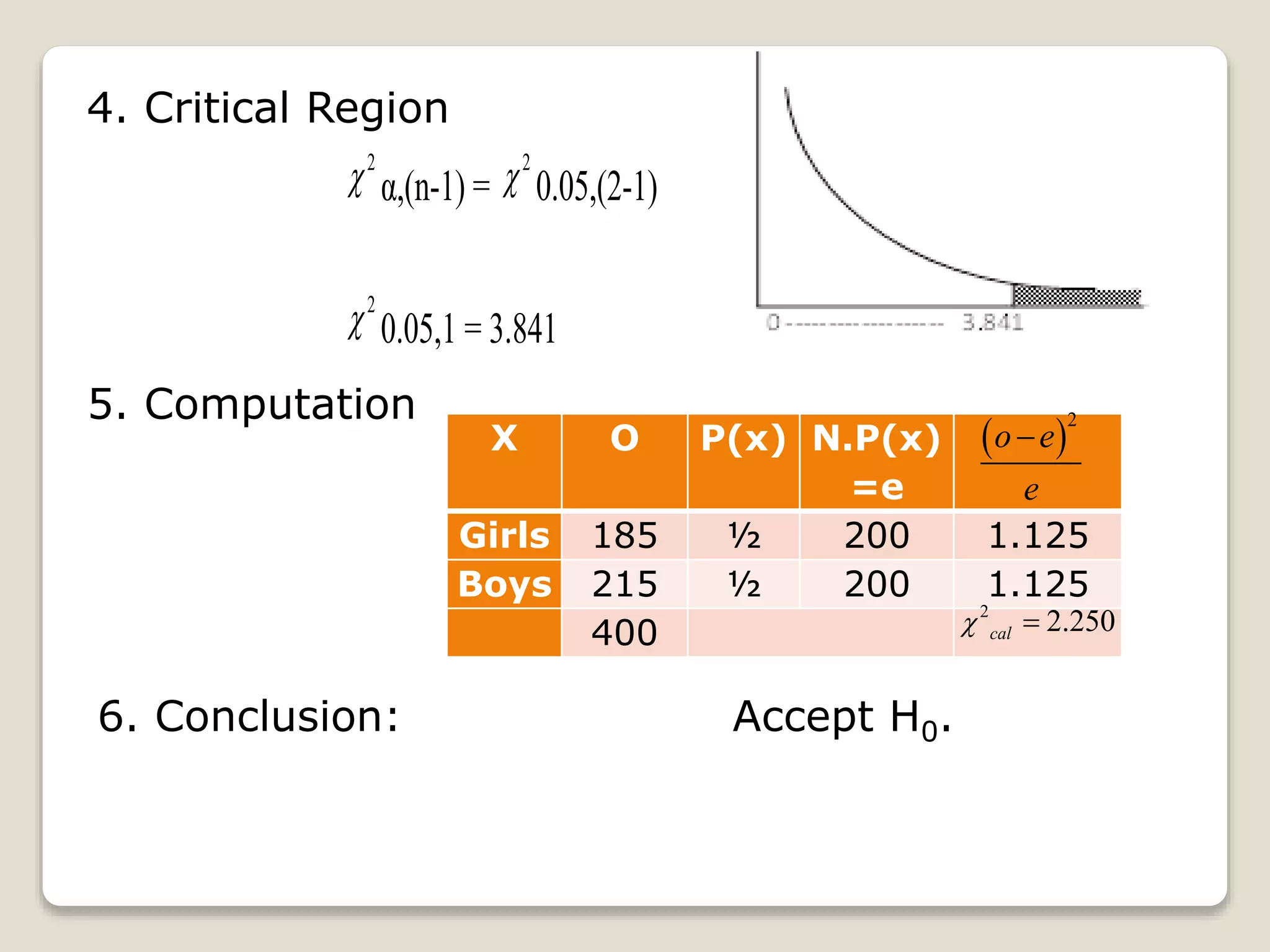
This document provides examples of using the chi-square goodness of fit test to analyze categorical data. It first explains the procedure for conducting the test, which involves defining hypotheses, determining the level of significance, calculating the test statistic, identifying the critical region, and making a conclusion. Then it provides three examples that demonstrate applying the test to analyze the distribution of grades, whether grades differ from a historical pattern, and whether the probability of boy and girl births is equal.

1. HYPOTHESIS
TESTING
Chi-Square Goodness of Fit Test:
NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Chi-Square Goodness of Fit Test:
This lesson explains how to conduct a chi-
square goodness of fit test. The test is
applied when you have one categorical
variable from a single population. It is
used to determine whether sample data
are consistent with a hypothesized
distribution.

3. Procedure Goodness of fit test
1-Hypothesis H0: Fit is good.
H1: Fit is not good.
2-Level of significance  = 1% or 5% or
any given value.
3-Test of statistic 𝜒2 =
𝑜−𝑒 2
𝑒
Where o = observed value
e = estimated value

4. 4-Critical region𝜒2
, 𝑛−1
5- Computation
6-Conclusion
If the calculated value of test
statistic falls in the area of
rejection, we reject the null
hypothesis otherwise accept it.

5. Example-8:
To investigate whether the following
distribution of grades is uniform at 5%
level of significance.
Grades A B C D E
F 25 30 22 32 15

6. Solution:
1- Hypothesis H0: Distribution of grades is uniform.
H1:Distribution of grades is not uniform.
2- Level of significance  = 0.05
3- Test of statistic 𝝌 𝟐
=
𝒐−𝒆 𝟐
𝒆
4- Critical region    
 
2 2
, 1 0.05, 5 1
2 2
0.05,4, 1
9.488
n
n


 
 
 


 
9.488

7. 5. Computation
X O P(x) N.P(x)=
e
A 25 1/5 24.8 0.0016
B 30 1/5 24.8 1.0903
C 22 1/5 24.8 0.3161
D 32 1/5 24.8 2.0903
E 15 1/5 24.8 3.8726
124
 
2
o e
e

2
7.371cal 
6. Conclusion: Accept H0.
(Distribution of grades is uniform)

8. Example-9:
Historical records indicate that in college students
passing in grades A,B,C,D and E are 10,30,40,10
and 10 percent, respectively. For a particular year
grades earned by students with grade A are 8,
17 with B, 20 with C, 3 with D and 2 with E. Using
 = 0.05 test the null hypotheses that
grades do not differ with historical pattern.

9. Solution:
1. Hypothesis
H0: Grades do not differ with historical pattern.
H1: Grades differ with historical pattern.
2- Level of significance  = 0.05
3- Test of statistic 𝝌 𝟐 =
𝒐−𝒆 𝟐
𝒆

10.    
 
2 2
, 1 0.05, 5 1
2 2
0.05,4, 1
9.488
n
n


 
 
 


  9.488
4- Critical Region
5. Computation
6. Conclusion: Accept H0.
(Grades do not differ with historical pattern).
X O P(x) N.P(x)=
e
A 8 0.10 5 1.80
B 17 0.30 15 0.27
C 20 0.40 20 0.00
D 3 0.10 5 0.80
E 2 0.10 5 1.80
50
 
2
o e
e

2
4.67cal 

11. Example-10:
In a survey of 400 infants chosen at random, it is
found that 185 are girls. Are boy and girl births
equally likely at  = 0.05
Solution:
1. Hypothesis
H0:Boy and girl births are equally likely
H1:Boy and girl births are not equally likely
2- Level of significance  = 0.05
3- Test of statistic 𝜒2 =
𝑜−𝑒 2
𝑒

12. 4. Critical Region
2
 α,(n-1) =
2
 0.05,(2-1)
2
 0.05,1 = 3.841
5. Computation
X O P(x) N.P(x)
=e
Girls 185 ½ 200 1.125
Boys 215 ½ 200 1.125
400
 
2
o e
e

2
2.250cal 
6. Conclusion: Accept H0.