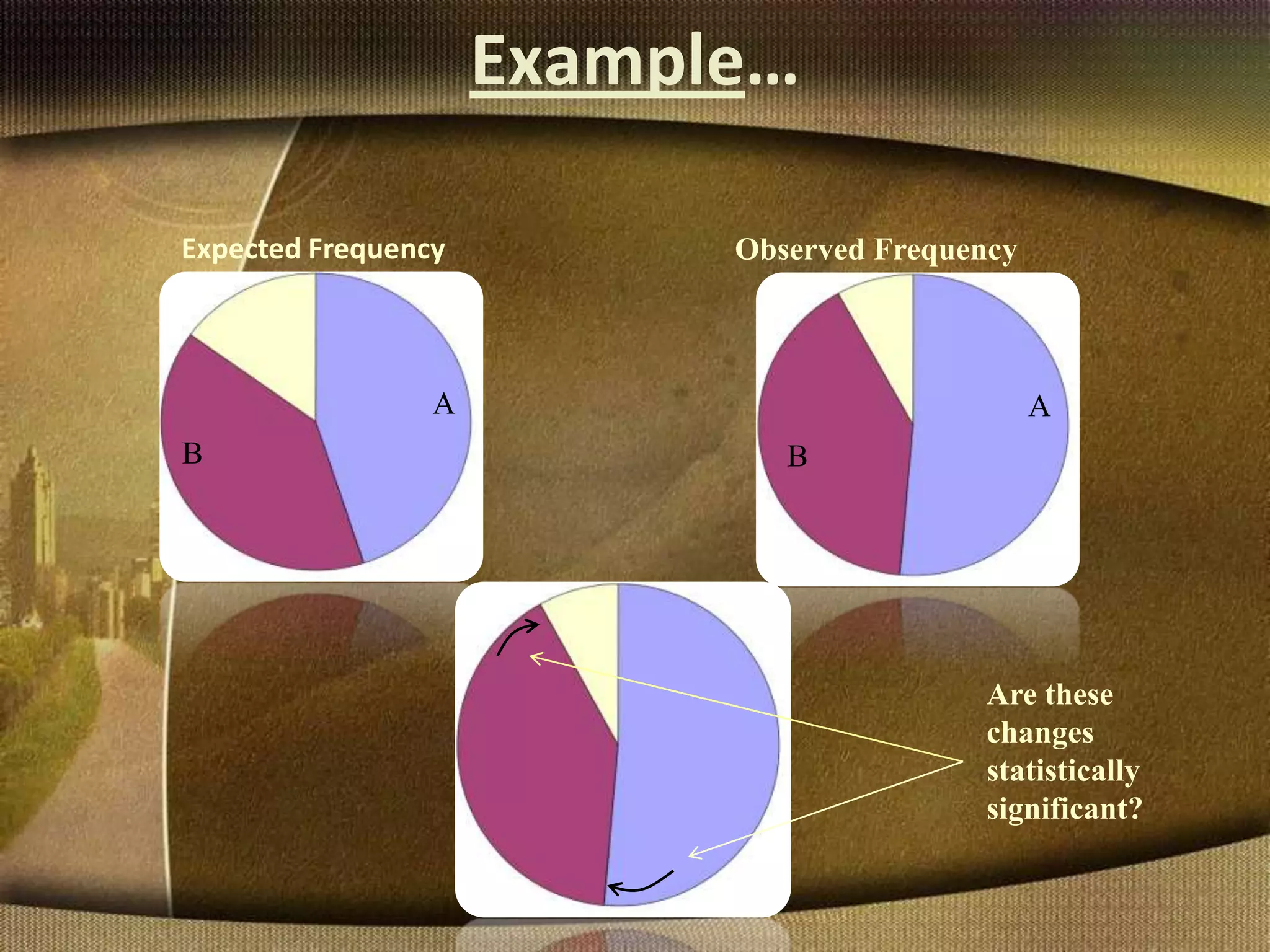
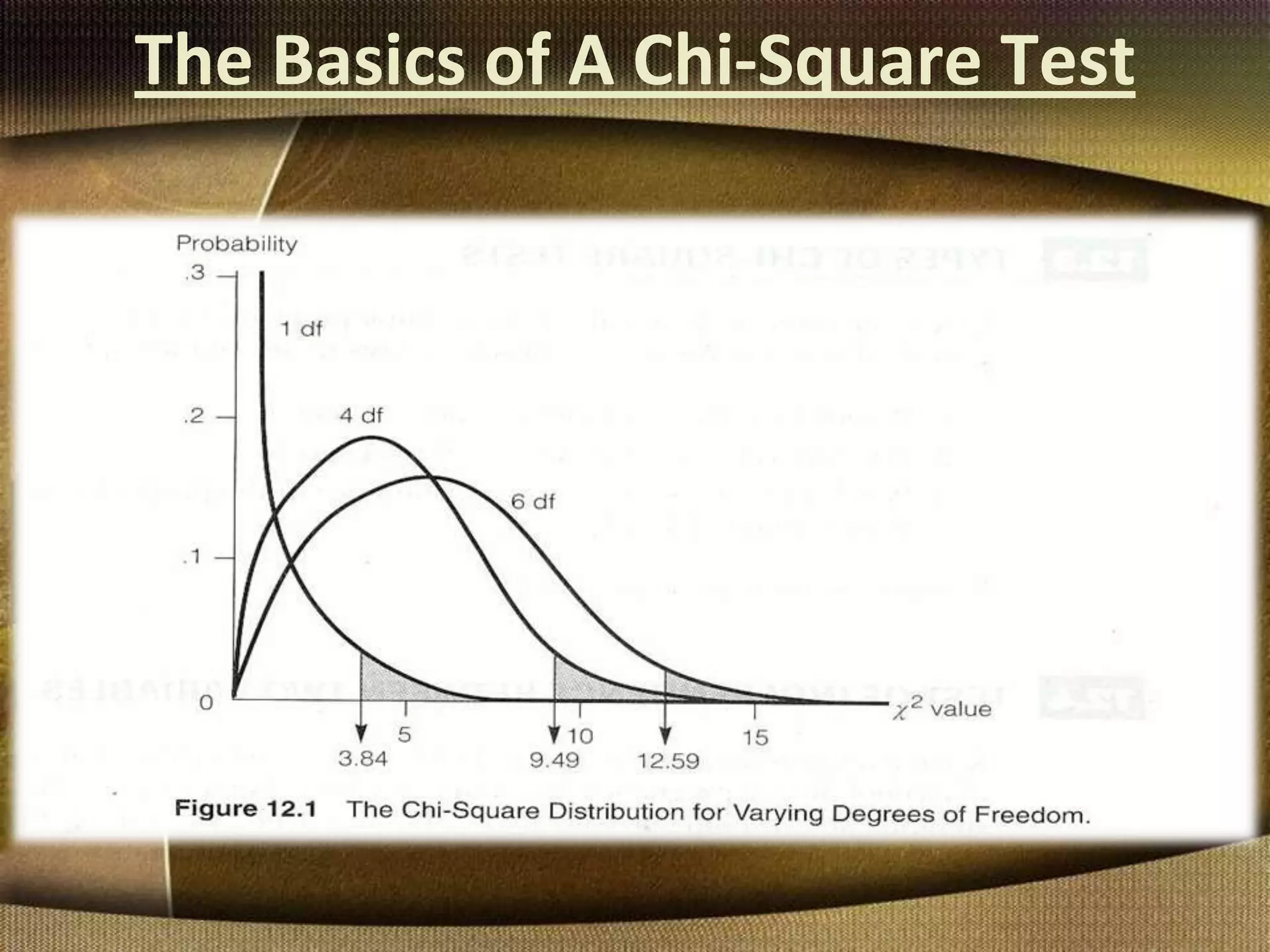
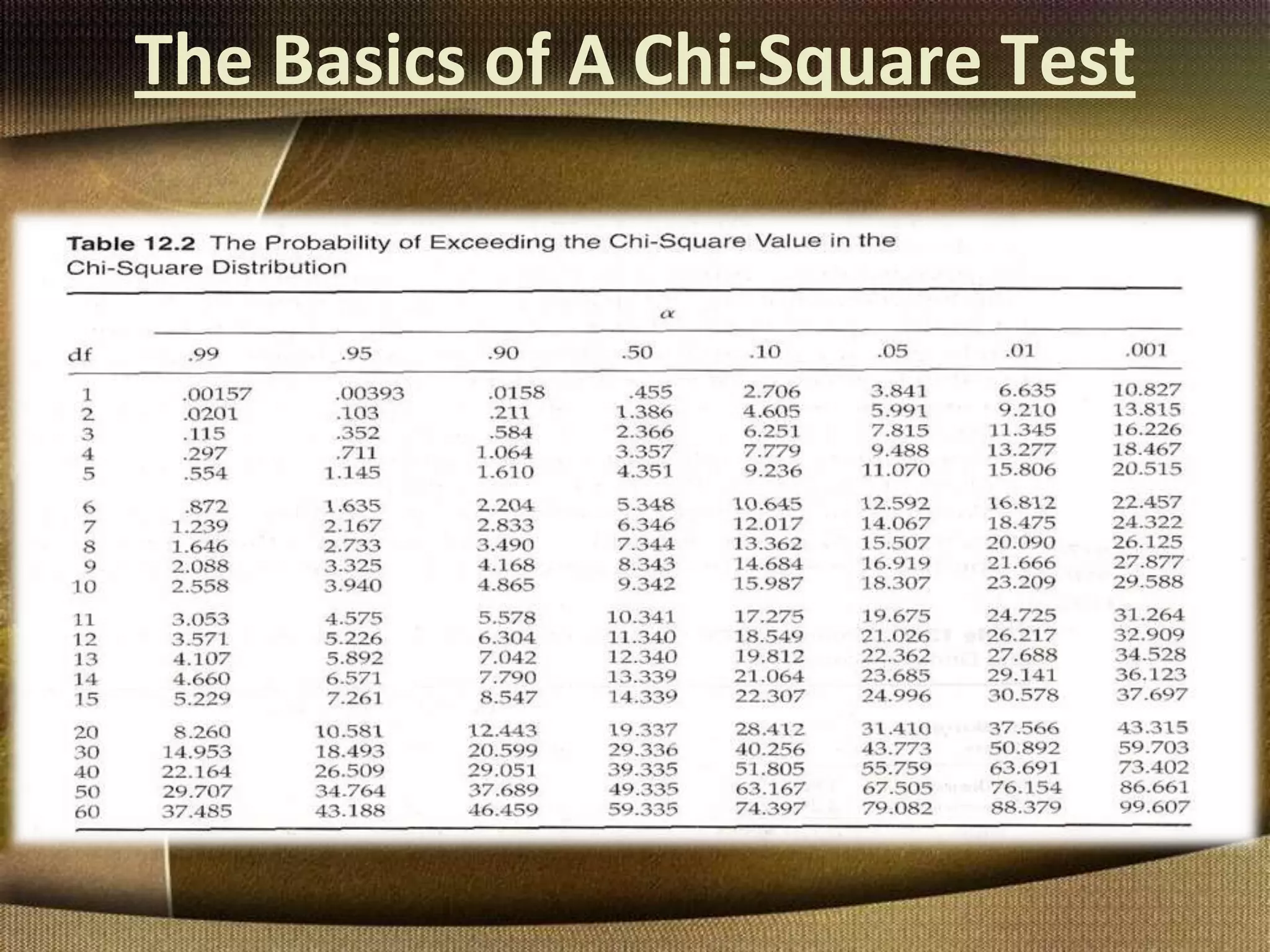
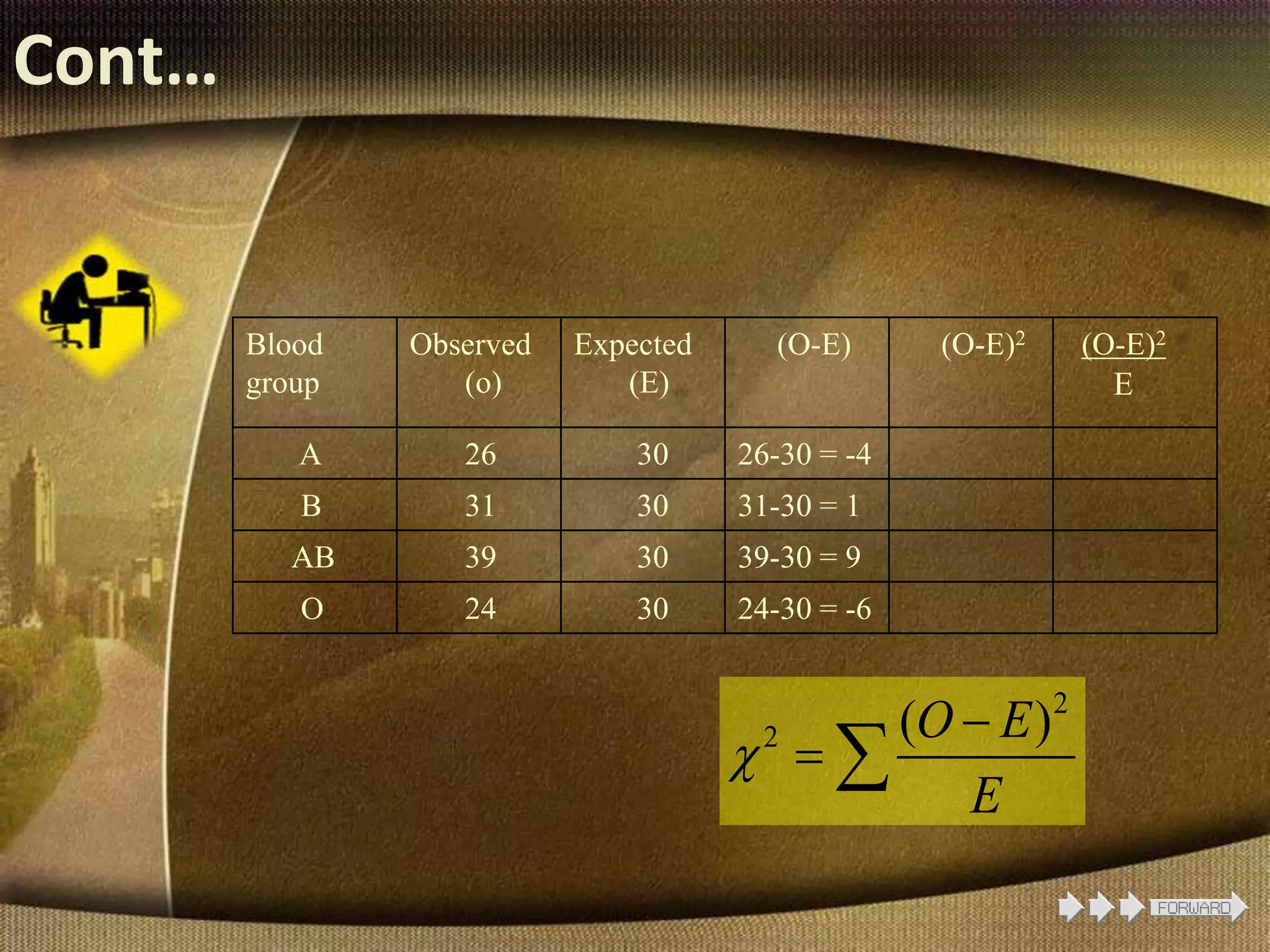
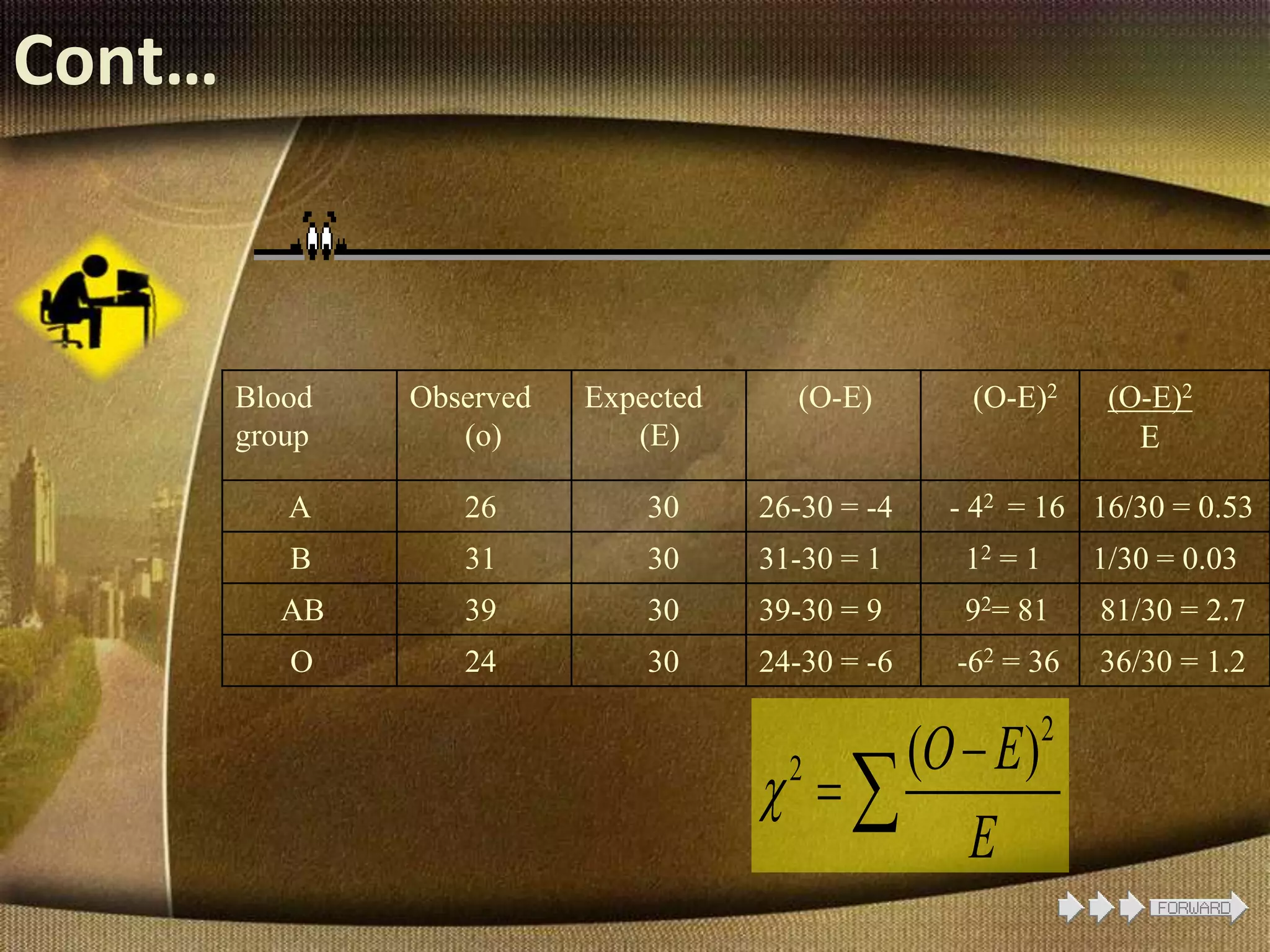
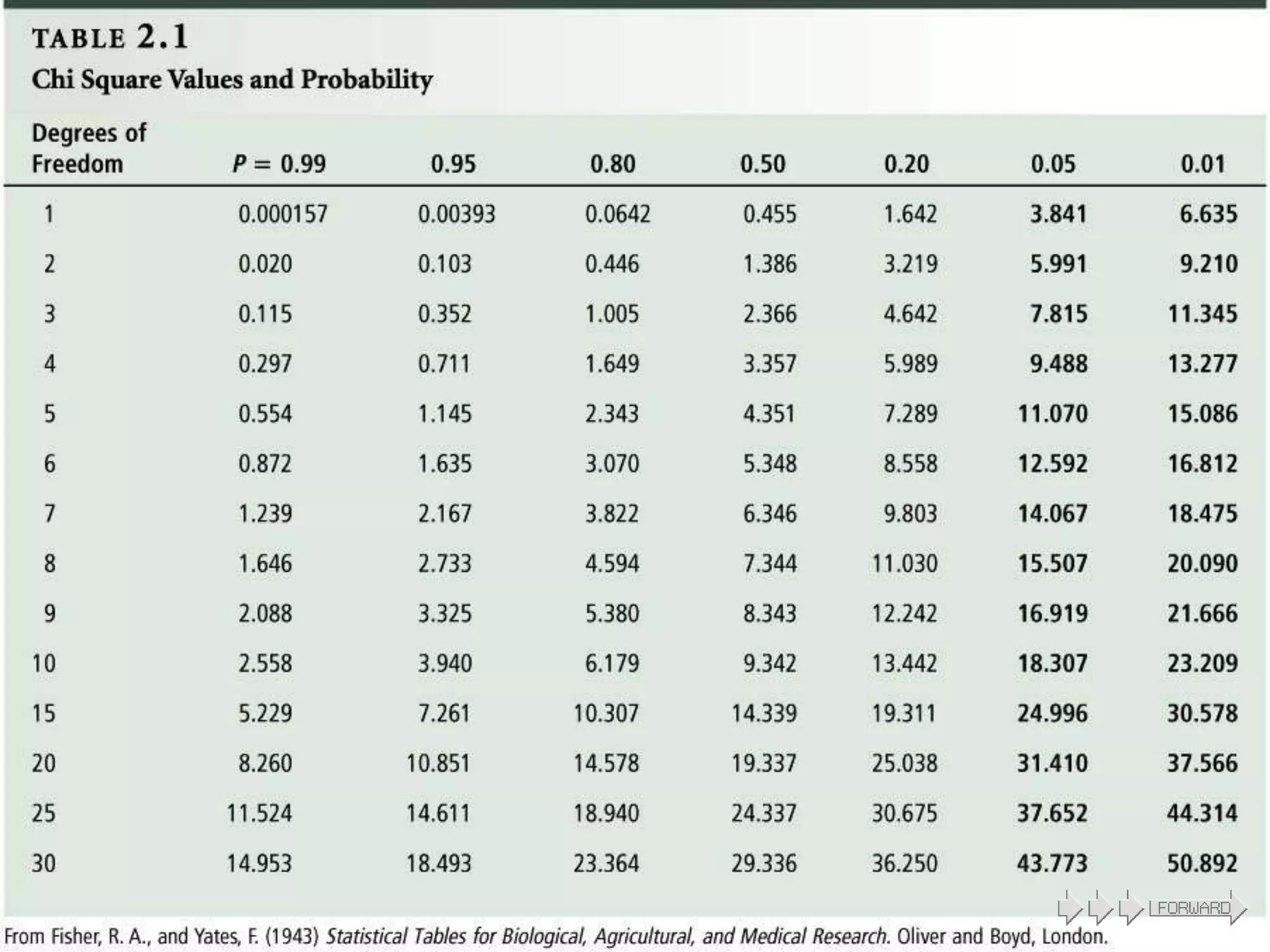
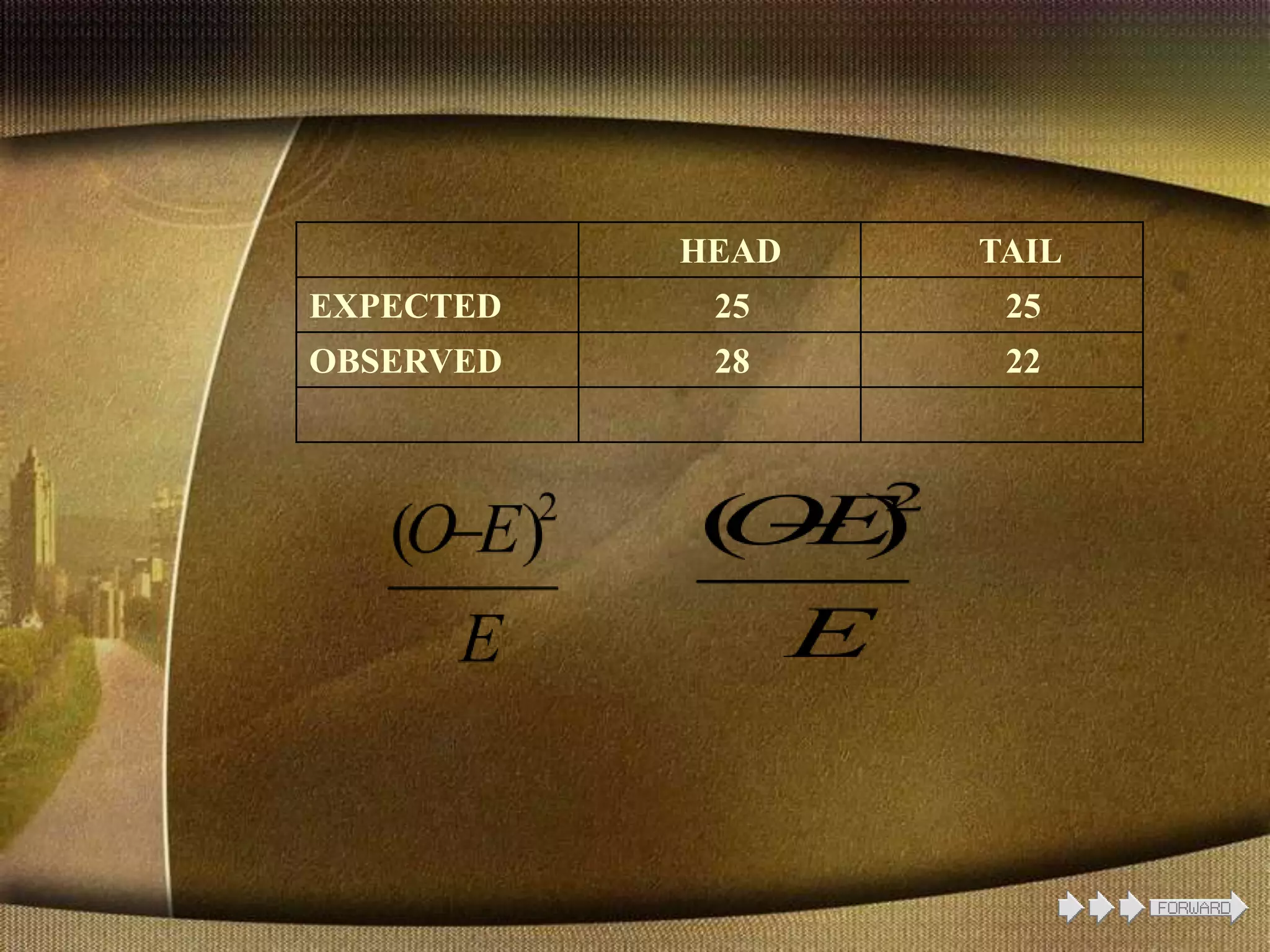
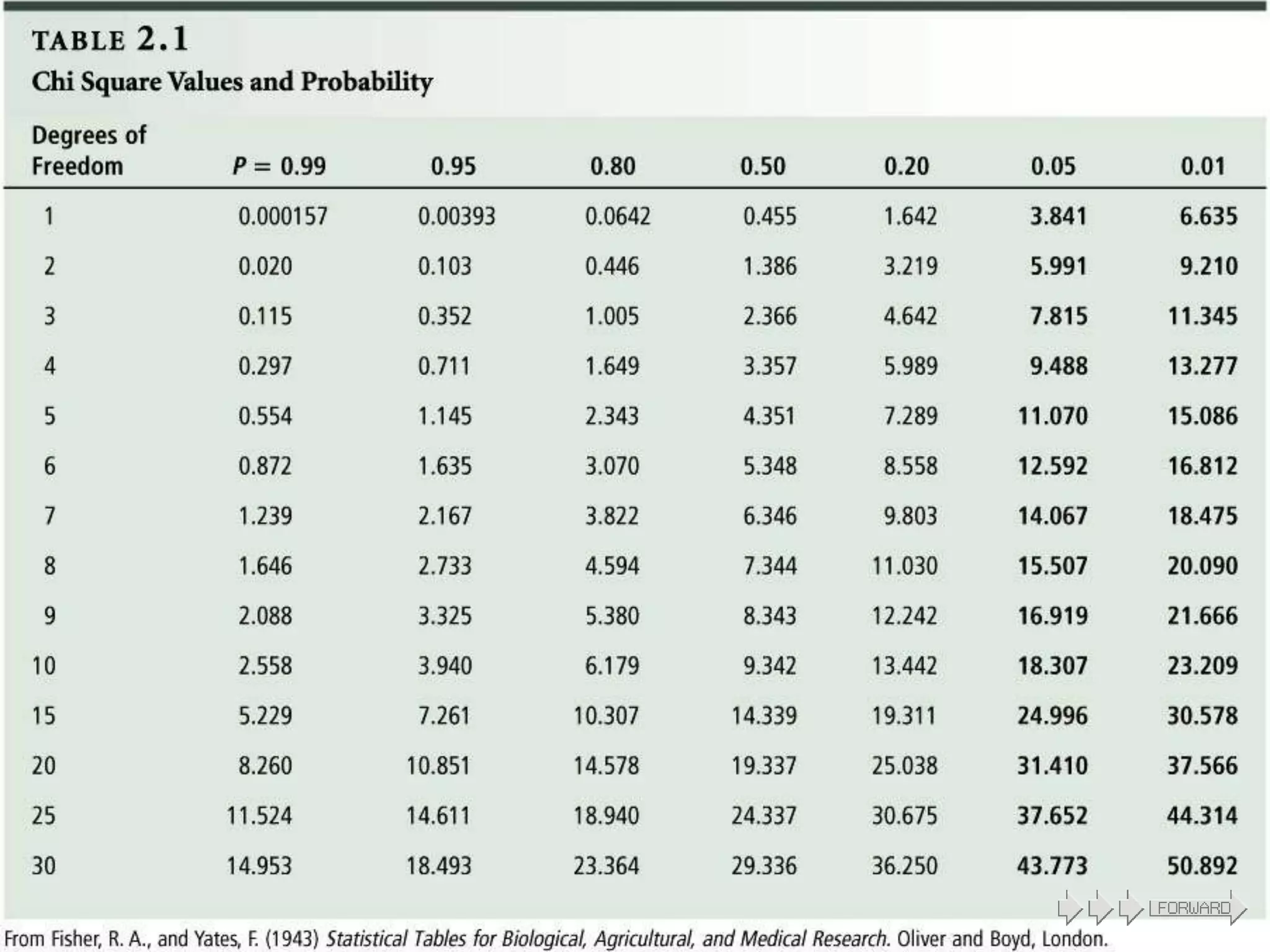
The document provides information about the chi-square test, including its introduction by Karl Pearson, its applications and uses, assumptions, and examples. The chi-square test is used to determine if an observed set of frequencies differ from expected frequencies. It can be used to test differences between categorical data and expected values. Examples shown include a goodness of fit test comparing blood group frequencies to expected equal distribution, and a one-dimensional coin flipping example.

2. CHI-SQUARE TEST
Presenter,
Dr.Syam Chandran.C
Dept of Shalakya Tantra
SDMCAH, Hassan

3. INTRODUCTION
•Karl Pearson(1880) introduced a test to
distinguish whether an observed set of
frequencies differs from a specified frequency
distribution
•A chi-square test, also referred to as chi-
squared test.
Karl Pearson

4. • “x” in Greek represents „chi‟ , square of this is „chi
square‟ or „ chi-squared test‟ .
• It is used to check the prevalence among the data.
• The chi-square test uses frequency data to generate
a statistical result
• Pearson's chi-squared test (χ2) is the best-known of
several chi-squared tests.

5. APPLICATION/UTILITY
• Chi square test is the test which tests
the significant difference between
expected value and observed value
which can be used for categorical data.
• OR, In simple words it is used to test
whether a significant difference exists
between the observed number of
samples and the expected number of
responses.

6. Parametric and Nonparametric Tests
• The term "non-parametric" refers to the fact that
the chi-square tests do not require assumptions
about population parameters nor do they test
hypotheses about population parameters.
• Some examples of hypothesis tests, such as the t
tests and ANOVA, are parametric tests and they
do include assumptions about parameters and
hypotheses about parameters.
6

7. Parametric and Nonparametric Tests
• The most obvious difference between the chi-
square tests and the other hypothesis tests we have
considered (t and ANOVA) is the nature of the
data.
• For chi-square, the data are frequencies rather
than numerical scores.
7

8. The Chi-Square Test for Goodness-of-Fit
• A statistical method used to determine goodness
of fit.
– Goodness of fit refers to how close the
observed data are to those predicted from a
hypothesis
Note:
– The chi square test does not prove that a
hypothesis is correct
• It evaluates to what extent the data and the
hypothesis have a good fit
8

9. The Chi-Square Test for Goodness-of-Fit
(cont.)
• The chi-square test for goodness-of-fit uses
frequency data from a sample to test hypotheses
about the shape or proportions of a population.
• Each individual in the sample is classified into one
category on the scale of measurement.
• The data, called observed frequencies, simply
count how many individuals from the sample are
in each category.

10. The Chi-Square Test for Goodness-of-Fit
(cont.)
• The null hypothesis specifies the proportion of the
population that should be in each category.
• The proportions from the null hypothesis are used
to compute expected frequencies that describe how
the sample would appear if it were in perfect
agreement with the null hypothesis.
10

11. Insight of chi-square Test
 Interpretation
 Rationale for the Chi-Square Test
 The Basics of a Chi-Square Test
 Types of Chi-Square Tests
 One dimensional example
 Two folded example
 Conclusion

12. INTERPRETATION
• If the difference of Observed value and
Expected value is zero or less, then there is no
significant difference. But, if the difference is
more then, there will be statistically
significant difference.

13. Rationale for the Chi-Square Test
• Various chi-square tests to deal with cases
involving frequency data
• Enumeration data
• Categorical data
• Qualitative data
• Contingency table

14. The Basics of A Chi-Square Test
• The chi-square test compares the observed
frequencies with the expected frequencies:
2
2 ( )O E
E


 
• Where
– O = observed data in each category
– E = expected data in each category based on the
experimenter’s hypothesis
– S = Sum of the calculations for each category

15. Chi Square Calculation
Each entry in the summation can be referred to as
“The observed minus the
expected, squared, divided by the expected”.
The chi square value for the test as a whole is
“The sum of the observed minus the
expected, squared, divided by the expected”

16.  




 

e
eo
F
FF 2
2 )(


17. Characteristics of the Chi-Square Distribution
1. It is not symmetric.

18. Characteristics of the Chi-Square Distribution
1. It is not symmetric.
2. The shape of the chi-square distribution
depends upon the degrees of freedom, just
like Student’s t-distribution.

19. Characteristics of the Chi-Square Distribution
1. It is not symmetric.
2. The shape of the chi-square distribution
depends upon the degrees of freedom, just
like Student’s t-distribution.
3. As the number of degrees of freedom
increases, the chi-square distribution
becomes more symmetric.

20. Characteristics of the Chi-Square Distribution
1. It is not symmetric.
2. The shape of the chi-square
distribution depends upon the degrees
of freedom, just like Student’s t-distribution.
3. As the number of degrees of freedom
increases, the chi-square distribution
becomes more symmetric.
4. The values are non-negative. That is, the
values of are greater than or equal to 0.

21. Example…
Expected Frequency
A
B
Observed Frequency
A
B
Are these
changes
statistically
significant?

22. The Basics of A Chi-Square Test
The chi-square value can occur easily by chance or
whether it is an unusual event that is unlikely to occur
by chance

23. The Basics of A Chi-Square Test

24. The Basics of A Chi-Square Test

25. Types of Chi-Square Test
Chi-square tests to determine the following:
• Whether the two variables are independent.
• Whether various subgroups are homogeneous.
• Whether there is a significant difference in the
proportions in the subclasses among the subgroups

26. Assumptions / Limitation in the
Use of Chi-Square
• Data is from a random sample.
• A sufficiently large sample size is required (at least
20)
• Observations must be independent.
• Actual count data (not percentages)
• Does not prove causality.

27. Determine Degrees of Freedom
df = k – 1
K = No : of categories

28. EXAMPLE
• In many families where the parents could have
produced children of all four blood groups, the total
number of children with each blood group was :
– Blood group A 26
– Blood group B 31
– Blood group AB 39
– Blood group O 24
– TOTAL 120

29. Cont…
Those numbers are the results observed and
have been put into the O column in this table

30. Cont.
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26
B 31
AB 39
O 24
2
2 ( )O E
E


 

31. Cont…
• Now we need to work out the expected results
• This is done by using the ratio that was described
before 1:1:1:1 ….

32. Cont…
• We just divide the total amount observed by 4.
120 / 4 = 30
• So we would expect to have 30 people of each
blood group…

33. Cont…
• Then we need to write that in the E column.

34. Cont…
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26 30
B 31 30
AB 39 30
O 24 30
2
2 ( )O E
E


 

35. Cont…
• Next we need to do O-E

36. Cont…
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26 30 26-30 = -4
B 31 30 31-30 = 1
AB 39 30 39-30 = 9
O 24 30 24-30 = -6
2
2 ( )O E
E


 

37. Cont…
• Then we square all the ( O – E) results…

38. Cont…
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26 30 26-30 = -4 - 42 = 16
B 31 30 31-30 = 1 12 = 1
AB 39 30 39-30 = 9 92= 81
O 24 30 24-30 = -6 -62 = 36
2
2 ( )O E
E


 

39. Cont…
Now, we divide all the ( O – E ) 2 results by E

40. Cont…
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26 30 26-30 = -4 - 42 = 16 16/30 = 0.53
B 31 30 31-30 = 1 12 = 1 1/30 = 0.03
AB 39 30 39-30 = 9 92= 81 81/30 = 2.7
O 24 30 24-30 = -6 -62 = 36 36/30 = 1.2
2
2 ( )O E
E


 

41. Cont…
• Finally , we add up the ( O – E)2 / E column…

42. Cont…
Blood
group
Observed
(o)
Expected
(E)
(O-E) (O-E)2 (O-E)2
E
A 26 30 26-30 = -4 - 42 = 16 16/30 = 0.53
B 31 30 31-30 = 1 12 = 1 1/30 = 0.03
AB 39 30 39-30 = 9 92= 81 81/30 = 2.7
O 24 30 24-30 = -6 -62 = 36 36/30 = 1.2
2
2 ( )O E
E


  4.46

43. Cont…
• So the result is 4.46
• Then we need to look up this result on
a probability table…

45. Cont…
• Before that we would have to work out
the degrees of freedom…

46. Cont…
• Which is always the amount of
possible phenotypes minus one.
So in this case 4 – 1 = 3

47. Cont…
• Then we find the 3 degrees of freedom row
and read along until we find the number
which is closest to our result…
• Finally we look which column this value is
in…

48. Cont…
• If its in the 0.05 (or 50 %) column or
any column less than this…
( meaning that the chi squared value is
bigger than the one in the 0.05 column)
• Then any differences are NOT due to
chance…
• Which means that something else is
affecting our results…

49. cont
So the null hypothesis is rejected…

50. cont
• But if its in a column above 0.05 (known as
the critical value)…
• (meaning that the chi squared value is
smaller than the one in the 0.05 column)
• Then any differences in our results are due to
chance…

51. Cont…
• And the null Hypothesis is accepted
• Remember that the critical value is
ALWAYS 0.05…

52. One-dimensional
• Suppose we want to flip 50 times a coin.
HEAD TAIL
EXPECTED 25 25
OBSERVED 28 22

53. HEAD TAIL
EXPECTED 25 25
OBSERVED 28 22

54. Cont…
25
)2528( 2

25
)2522( 2

+
25
9
+
25
18
= 72.0
25
9

55. • Degree of freedom
K – 1
2 – 1 = 1

57. Cont…
• In this case the critical value is 3.841
• We got a value 0.72 which is lower than
the critical value, so we accept null
hypothesis.
• If the value is more than the critical value
we got , then we reject the null hypothesis.

58. SOME AYURVEDIC JOURNALS
USING CHI SQUARE
• Allopathic vs. Ayurvedic practices in tertiary care
institutes of urban North India
(Indian Journal of Pharmacology, Vol. 39, No. 1,
January-February, 2007, pp. 52-54).
• Assessment of oligospermia with special reference to
rakta dusti.
(International research journal of Pharmacy 2012)
• Evaluation of efficacy of karshaneeya yavagu (An
Ayurvedic preparation) in the management of
Obesity.
(International Journal of Research in Ayurveda &
Pharmacy;Mar2012, Vol. 3 Issue 2, p295)

59. Conclusion
• Note that all we really can conclude is that our data
is different from the expected outcome given a
situation
– Regardless of the position of the frequencies
we’d have come up with the same result
– It is a non-directional test regardless of the
prediction.