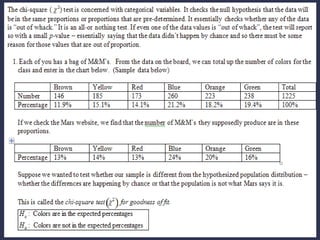
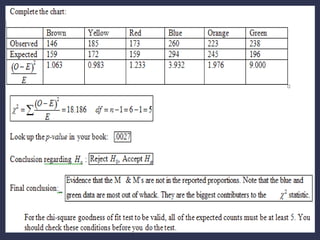
The chi-square goodness of fit test is utilized for qualitative data from a single population to assess if sample data aligns with a hypothesized distribution. The process involves stating hypotheses, formulating an analysis plan, analyzing data to obtain test statistics and p-values, and interpreting results to either accept or reject the null hypothesis. Key requirements include a simple random sample, an adequate population size, and a minimum expected value of observations.

1. Chi-Square
Goodness of Fit Test

2. Chi- Square Goodness of Fit test
• This test is applied when you have qualitative data
from one single population
• Used to determine whether sample data is
consistent with the hypothesized distribution
– Example: If the M&M CO. claimed that 30% of M&M’s
were red, 40% green, 10% brown, 10% blue and 10%
yellow, we could gather random samples of M&M’s and
determine whether our distribution was different than
the claim made from the company

3. Conditions
• Simple Random Sample
• The population size is at least 10 times greater
than the sample size
• The variable of the study is qualitative
• The expected value of the sample
observations in each level of the variable is at
least 5.

4. Conducting a Hypothesis Test
1- State Hypothesis: Ho & Ha must be mutually exclusive
Ho: data consistent with a particular distribution
Ha: data that are not consistent with a particular distribution
* usually Ho specifies the proportion of observations at each level of
the variable. The alternative hypothesis states that at least one of
the specific proportions is not true
2- Formulate an Analysis Plan
- describes how the sample data is used towards the null hypothesis
* use the chi square goodness of fit test. It is used to determine if
the observed frequencies differ significantly from the expected
frequencies stated in the null hypothesis.

5. 3- Analyze: using sample data, find the degrees of
freedom(DF), expected frequency counts, test statistics, and P-
value corresponding to the TS)
* DF= k-1 k= # of levels of the qualitative variable
*Expected Frequency counts:
E= np E= expected frequency counts
n= sample size
p= hypothesized proportion from the null
hypothesis
*TS: Chi- Square random variable:
O= observed frequency count
E= expected frequency count
*P- value- probability of observing the sample statistic as extreme as the TS where the TS
is a chi square with degrees of freedom)
(can be found using Table C)
4- Interpret: Given the null hypothesis, if the sample results are
unlikely, then reject the null. (done by comparing the P-value to the
significance level and rejecting the null hypothesis if the P-value is
less than the significant level)